Het novembernummer van Pythagoras bracht een opgave van de Mathekalender van 2015. Vier kabouters krijgen een muts op met elk een ander getal erop. De kabouters zien wel de getallen op de mutsen van de andere drie, maar niet dat op hun eigen muts. Dan moeten ze alle vier, zonder te zien wat hun collega’s doen, hun linkerhand of hun rechterhand opsteken. Als de kabouters met het kleinste en het op twee na kleinste getal dezelfde hand opsteken en de andere twee kabouters allebei de ándere hand opsteken, dan winnen ze een prijs. Vooraf mogen ze overleggen over een strategie, maar vanaf het moment van het zien van elkaars getallen stopt alle onderlinge communicatie.

Vier mutsen kunnen op 4 $\times$ 3 $\times$ 2 $\times$ 1 = 24 mogelijkheden over de vier kabouters verdeeld worden. Op deze 24 permutaties was klaarblijkelijk de oorspronkelijke vraagstelling in de Mathekalender gebaseerd. Die luidde: hoe groot is de kans dat de kabouters de prijs winnen? Je kon kiezen uit tien antwoorden, alle een breuk met noemer 24. Pythagoras maakte het zijn lezers wat makkelijker. Het verklapte dat de kabouters altijd kunnen winnen. Het correcte antwoord was dus 24/24.

De oplossing in het januarinummer maakte gebruik van een tabel, waarbij de 24 permutaties van 4 objecten op een intrigerende wijze geordend zijn. Maar wat doen kabouters die deze tabel niet kennen? Die beraden zich op een andere oplossing.

Om het handopsteken geen gokpartij te laten zijn, is een afspraak nodig. Tenminste één kabouter moet de andere drie inlichtingen verschaffen over wat hij gaat doen. En tegelijk daarmee proberen ze zoveel mogelijk nuttige informatie over te dragen.

Afgesproken wordt daartoe dat kabouter D zijn handopsteken zal verdelen, al naar gelang de volgorde van de getallen die hij bij de andere drie ziet. Er zijn er zes, en die kun je verdelen in twee groepjes van drie. Niet elke verdeling is nuttig. Als bijvoorbeeld ABC en ACB bij ‘dezelfde hand’ van D zijn ingedeeld, dan heeft B een keuzeprobleem als D tussen A en C ligt. Na overleg wordt afgesproken: als D, naar oplopende grootte, de volgorde (1) ABC, (2) CAB of (3) BCA waarneemt, dan zal hij R(echts) opsteken; ziet hij (4) CBA, (5) BAC of (6) ACB, dan L(inks).

Deze indeling heeft bijzondere eigenschappen. Het groepje (1) tot en met (3) is cyclisch, d.w.z. je kunt (2) uit (1) krijgen door de laatste van drie letters te verplaatsen naar de eerste positie; net zo kun je (3) uit (2) krijgen; en (1) weer uit (3). De drie zijn dus volkomen gelijkwaardig. Hetzelfde is het geval bij het tweede groepje, ook dat is cyclisch. Merk op dat (4) het ‘omgedraaide’ (of: het gespiegelde ten opzichte van de middelste letter) is van (1); evenzo (5) van (2), en (6) van (3).

Hoe werkt deze strategie? We geven een voorbeeld. Stel, de getallen op de mutsen van A, B, C en D zijn achtereenvolgens 17, 25, 38, 23. B kan zien dat A < C, en daaruit opmaken dat D alleen (1), (5) of (6) gezien kan hebben. Als D (1) zag, zal hij R opsteken; B kan zien dat hij zich dan samen met D ‘tussen’ A en C bevindt, en zal dus L moeten kiezen. Als D (5) of (6) gezien heeft, zal hij L kiezen, maar B ziet dat ook hij in deze twee gevallen L moet kiezen. En welk viertal getallen we ook proberen, steeds weer blijkt dat A, B en C eenduidig kunnen concluderen welke hand ze moeten opsteken. Het kost niet heel veel moeite om alle varianten na te gaan: steeds is het in orde. En daarmee zouden we klaar zijn: de strategie werkt. Maar we willen graag weten waaróm.

Min maal min is plus

Een antwoord is het volgende. Laten we het opnieuw eens bekijken vanuit het standpunt van B. Hij ziet de volgorde van A, C en D. Zijn positie ten opzichte van D weet hij niet, maar hij kan de mogelijkheden inventariseren, en daarmee het gevolg ervan: of hij dezelfde hand als D moet opsteken, of niet dezelfde. Dit schema is:

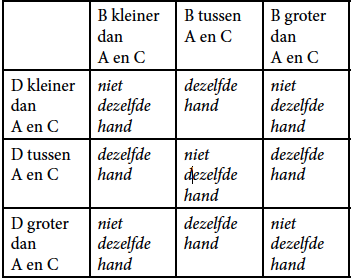
Hieruit ziet B dat als hij ‘tussen’ A en C ‘zit’, hij het tegengestelde moet doen van wat hij moet doen als hij hetzij kleiner, hetzij groter is dan A en C. Als we nu teruggaan naar ons getallenvoorbeeld, zien we dat de volgorde waarin B in het midden staat, ABC, in z’n eentje bij R staat, en de andere twee samen bij L. Dat komt prima uit! Want omdat D bij (1) de andere hand opsteekt dan bij (5) en (6), is het resultaat dat B nu in alle drie gevallen dezelfde hand kan opsteken. ‘Min maal min’ maakt ook hier ‘plus’. Dit blijkt niet alleen te gelden voor dit specifieke geval (A < C), maar – op grond van de mooie eigenschappen van de groepjes (1) tot en met (3) en (4) tot en met (6) – ook als A > C; voor de gevallen A < B en A > B (dit is van belang voor C); en voor B < C en B > C (van belang voor A). Deze oplossing maakt dus ook gebruik van spiegelingen en weerkaatsingen; maar is nu in elkaar geknutseld door de kabouters zelf.

Terzijde: A, B en C kunnen elk vrij kiezen uit één van de drie volgordes die D hun aanreikt. voor het resultaat maakt dat immers geen verschil. Kiezen ze alle drie de volgorde waarin zij de kleinste zijn, en voegen zij D daar op de juiste positie in, dan komt dat min of meer overeen met de oplossing in het januarinummer. En... de geheugenbelasting van de kabouters is gering: ze hoeven weinig meer te onthouden dan ‘ABC – rechts, CBA – links’.

Vijf kabouters

Als de kabouters na hun eigen denkwerk de oplossing in het januarinummer lezen, zijn ze eerst verwonderd, maar al snel zien ze gelijkenis. Zelfs zozeer, dat ze zich afvragen: ‘Als wij met ons ‘lichte’ schema het probleem voor ons vieren konden oplossen, zouden we dan met het ‘zware’ schema van het januarinummer niet het probleem kunnen oplossen voor vijf kabouters, die hun hand ‘om en om’ (dus LRLRL of RLRLR) moeten opsteken?’ Dat kan vast. Kun jij bedenken hoe?