Op de middelbare school leer je kwadratische vergelijkingen oplossen volgens drie methoden. Je herleidt de vergelijking eerst altijd tot nul. Je kijkt dan of je hem kunt ontbinden in factoren. Als dat niet lukt, kun je kwadraat afsplitsen. Of je past de abc-formule toe. 

De abc-formule krijg je door kwadraat afsplitsen toe te passen op de algemene kwadratische vergelijking $ax^2 + bx + c = 0$, waarvan de oplossingen zijn:

$$x=\frac{-b\pm\sqrt{D}}{2a}\mbox{ met }D=b^2-4ac.$$

Hoezo b² – 4AC?

Handig van de abc-formule is dat je via de discriminant $D$ kunt uitzoeken of de vergelijking twee, één of geen oplossing(en) heeft. Nadeel is dat de abc-formule door letterrekenen is afgeleid en daarom weinig betekenis heeft. Waar komt $b^2 - 4ac$ vandaan?

Onthoud je de formule verkeerd, dan kom je helaas niet bij de juiste oplossingen uit. 

Als je goed kijkt naar de abc-formule zie je misschien dat er wel enige samenhang is met wat je hebt geleerd over parabolen. Bij een kwadratische formule met de vorm $y = ax^2 + bx + c$, weet je immers dat daar een parabool bij hoort met de symmetrie-as $x=-\frac{b}{2a}.$ Die $-\frac{b}{2a}$ is ook de $x$-coördinaat van de top van de parabool. Dat is immers het enige punt van de parabool dat op de symmetrie-as ligt. 

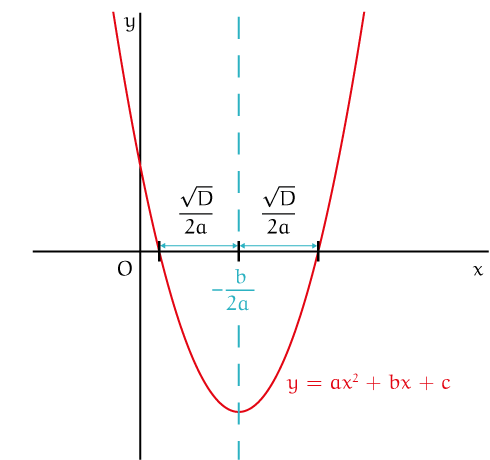
Los je de vergelijking $ax^2 + bx + c = 0$ op, dan bereken je de snijpunten van de parabool met de $x$-as. En als je de abc-formule iets anders schrijft, zie je dat de twee snijpunten met de $x$-as symmetrisch zijn ten opzichte zijn van $-\frac{b}{2a}$.

Want $x=\frac{-b\pm\sqrt{D}}{2a}$ kun je ook schrijven als $x=-\frac{-b}{2a}\pm\frac{\sqrt{D}}{2a}$.

Kennelijk is de afstand van de nulpunten tot de symmetrie-as altijd gelijk aan $\frac{\sqrt{D}}{2a}$. Zie figuur 1.

We laten de abc-formule voor wat hij is. We hebben hem verder niet meer nodig.

De symMetriEmethode

De symmetriemethode maakt gebruik van de symmetrie van de parabool en het vinden van oplossingen via ontbinden in factoren. Hoe ging dat ook alweer met ontbinden in
factoren? Je hebt bijvoorbeeld de kwadratische vergelijking $x^2 + 5x + 6 = 0$. 

Je kunt deze ontbinden in factoren via de product-som-methode. Je gaat op zoek naar twee getallen waarvan het product gelijk is aan $6$ en de som gelijk is aan $5$. Je vindt de getallen $2$ en $3$ en mag dus schrijven $(x + 2)(x + 3) = 0$ want deze vergelijking is equivalent met $x^2 + 5x + 6 = 0$. 

Je hebt nu ontbonden in factoren. Volgens het principe $A \cdot B = 0$ dus $A = 0$ of $B = 0$ vind je de oplossingen: $x + 2 = 0$ of $x + 3 = 0$ en dus: $x = -2$ of $x = -3$.
Merk op dat als de gevonden getallen positief zijn, de oplossingen negatief zijn.

We gaan deze aanpak veralgemeniseren met letters. We noemen de oplossingen van de vergelijking $x_1$ en $x_2$, en kunnen de vergelijking $ax^2 + bx + c = 0$ dus schrijven als: $$a(x - x_1)(x - x_2) = 0.$$

We gaan voor het oplossen van de vergelijking weer even uit van de vorm $ax^2 + bx + c = 0$. Om de product-sommethode toe te passen delen we alles door $a$. Je krijgt dan 

$$x^2+\frac{b}{a}x+\frac{c}{a}=0.$$

Er geldt voor het product: $-x_1\cdot -x_2=\frac{c}{a}$ en dus $x_1\cdot x_2=\frac{c}{a}$.

En voor de som geldt: $-x_1+-x_2=\frac{b}{a}$ en dus $x_1+x_2=-\frac{b}{a}$.

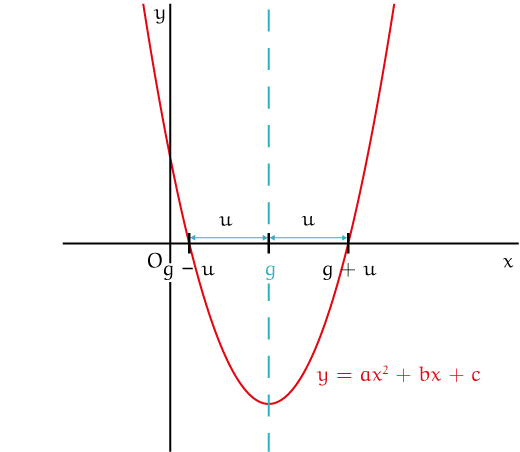
We gaan de oplossingen van de vergelijking nu anders schrijven. We weten immers dat deze symmetrisch zijn ten opzichte van de symmetrie-as. De $x$-coördinaat van deze symmetrie-as noemen we $g$ van gemiddelde. En de afstand tussen de nulpunten en de symmetrie-as noemen we $u$ van uitwijking. Zie figuur 2.

Er geldt dan dus: $x_1 = g - u$ en $x^2 = g + u$. We gaan deze waarden invullen in de som: $x_1+x_2=-\frac{b}{a}$ geeft $g-u+g+u=-\frac{b}{a}$ en dus $2g = -\frac{b}{a}$ en dus $g=-\frac{b}{2a}$. We hebben met deze formule nu dus langs andere weg de symmetrie-as gevonden.

Nu gaan we kijken naar het product: $(g-u)(g+u)=\frac{c}{a}$, we herkennen in het linkerlid het merkwaardig product en kunnen dus direct schrijven: $g^2-u^2=\frac{c}{a}$.

Voorbeeld 1

Bekijk nog eens $x^2 + 5x + 6 = 0$. Er staat een $1$ voor $x^2 (a = 1)$, je hoeft dus niet eerst te delen. 

De beide oplossingen zijn: $x_1 = g - u$ en $x_2 = g + u$. Voor de som geldt dus: $(g - u) + (g + u) = -5$ en dus $g=-\frac{5}{2}$.

Er geldt voor het product $(g - u)(g + u) = 6$ ofwel $g^2 - u^2 = 6$. We vullen de waarde van $g=-\frac{5}{2}$ in en vinden $\left(-\frac{5}{2}\right)^2-u^2=6$.

Dat geeft:

$$u^2=\left(-\frac{5}{2}\right)^2-\frac{6}{1}=\frac{25}{4}-\frac{24}{4}=\frac{1}{4}.$$

En dus $u = \frac{1}{2}$ of $u=-\frac{1}{2}$.

Merk op: omdat $u$ een afstand is, gebruiken we de positieve waarde (maar de negatieve waarde zou natuurlijk dezelfde oplossing geven). We vinden inderdaad de oplossingen $x_1=-\frac{5}{2}-\frac{1}{2}=-3$ en $x_2=-\frac{5}{2}+\frac{1}{2}=-2$.

Voorbeeld 2

Laten we het eens proberen met een vergelijking die niet geheeltallig te ontbinden is:

$$x^2+x-1=0.$$

Dan is

$g=-\frac{b}{2a}=-\frac{1}{2\cdot 1}=-\frac{1}{2}$ en $g^2-u^2=\frac{c}{a}=-1$.

Invullen van $g$ geeft $\left(-\frac{1}{2}\right)^2-u^2=-1$ en dus

$$u^2=\left(-\frac{1}{2}\right)^2+1=\frac{1}{2}+1=\frac{5}{4}.$$

En dus $u=\sqrt{\frac{5}{4}}=\frac{\sqrt{5}}{\sqrt{4}}=\frac{1}{2}\sqrt{5}$.

De oplossingen zijn $x_1=-\frac{1}{2}-\frac{1}{2}\sqrt{5}$ en $x_2=-\frac{1}{2}+\frac{1}{2}\sqrt{5}$.

Voorbeeld 3

Tot slot kijken we naar een vergelijking die geen oplossingen heeft (check de discriminant maar). Neem $2x^2+x+1=0$.

Er geldt $g=-\frac{b}{2a}=-\frac{1}{4}$ en $g^2-u^2=\frac{c}{a}=\frac{1}{2}$.

Invullen van $g$ geeft $\left(-\frac{1}{4}\right)^2-u^2=\frac{1}{2}$ en dus

$$u^2=\left(-\frac{1}{4}\right)^2-\frac{1}{2}=\frac{1}{16}-\frac{8}{16}=-\frac{7}{16}.$$

We kunnen de wortel uit een negatief getal niet trekken. En dus zijn er inderdaad geen oplossingen.

	Opgaven Los de volgende vergelijkingen op met de symmetriemethode. $x^2+3x+1=0$ $4x^2+8x-5=0$ $8x^2-6x+1=0$ $2x^2-5x-15=0$

 

Op YouTube vertelt de Amerikaanse wiskundige Po-Shen Loh over de symmetriemethode. 

Wil je zien hoe hij hem zelf uitlegt met voorbeelden? Kijk dan naar www.youtube.com/watch?v=XKBX0r3J-9Y&t=1525s
of gebruik binnen Youtube de zoektermen 'quadratic equation Po-Shen Loh'.