Oplossing Kleine Nootjes 58-6
Rare breuken
De oplossingen zijn $1 \frac{22}{11} = 3$ en $777 \frac{777}{777} = 778.$
Van 1234 naar 4321
| 0) | Startsituatie | 1 | 2 | 3 | 4 |
| 1) | Pak 1 op en leg die 2 naar rechts op 3 | - | 2 | 31 |
4 |
| 2) | Pak 4 op en leg die 1 naar links op 1 | - | 2 | 314 | - |
| 3) | Pak 4 op en leg die 2 naar links | 4 | 2 | 31 | - |
| 4) | Pak 1 op en leg die 2 naar links | 41 | 2 | 3 | - |
| 5) | Pak 2 op en leg die 1 naar links | 412 | - | 3 | - |
| 6) | Verschuif 3 1 naar links | 412 | 3 | - | - |
| 7) | Pak 2 op en leg die 3 naar rechts | 41 | 3 | - | 2 |
| 8) | Verschuif 2 1 naar links | 41 | 3 | 2 | - |
| 9) | Pak 1 op en leg die 3 naar rechts | 4 | 3 | 2 | 1 |
Dus in 9 beurten lukt het.
Splitsen in drieën met drie
a) De kleinste oplossing is $n = 5, a = 1, b = 3$ en $c = 1 : 3 \times 1 + 3/3 + 1 = 5.$
b) Voor $n = 99$ zijn er twee oplossingen:
b1) $a = 22, b = 75$ en $c = 2 : 3 \times 22 + 75/3 + 2^3 = 99;$
b2) $a = 15, b = 81$ en $c = 3 : 3 \times 15 + 81/3 + 3^3 = 99.$
Hardlopen
Als Cato $5$ rondjes loopt, loopt Joepie er $4.$ Hun snelheden verhouden zich dus als $5 :4$. Dus $v_C = (5/4)v_J$ en $v_C = v_J + 2.$ Dat geeft: $v_J = 8$ km/u en $v_C = 10$ km/u. Cato legt haar $2$ km af in $2/10$ uur, is $12$ minuten. Joepie legt zijn $2$ km af in $2/8$ uur, is $15$ minuten.
Joepie moet dus nog $3$ minuten lopen.
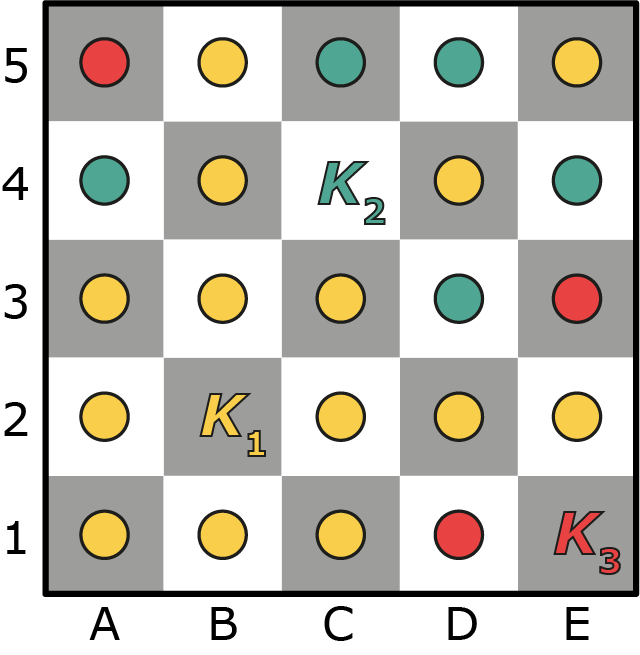
Koninginnen op een schaakbord
Je hebt drie koninginnen nodig. Zie de figuur.