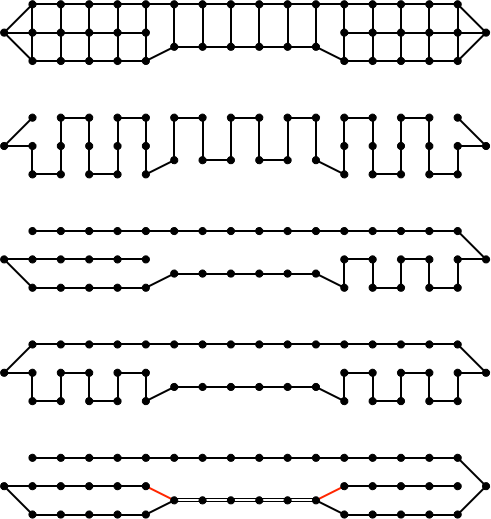
Micro wilde graag leren poetsen zoals Phi en Pi dat zo handig doen met hun elektrische tandenborstel. Maar Phi gaf het recept niet zomaar prijs.  Het werd een ontdekkingsreis. Eerst eens een plaatje tekenen van het bovengebit met alle vlakken van tanden en kiezen die gepoetst moeten worden (het ondergebit is hetzelfde). Elk vlak is met een vette punt weergegeven in het bovenste diagram.

Een lijntje tussen twee punten betekent dat je met de borstel zonder optillen van dat ene vlak naar het andere kunt doorpoetsen. Dit is een gebit met verstandskiezen. Als je die niet hebt moet je het diagram aan beide uiteinden inkorten. Je ziet dat de kiezen behalve het vooren achtervlak ook een kauwvlak hebben. En op de uiteinden zijn er zijvlakken, die je natuurlijk ook moet poetsen.

De kunst is om in dat diagram een pad langs de lijntjes te vinden dat precies één keer langs elk punt (vlak) komt. Dit wordt wel een Hamiltonpad genoemd. Hamilton was een Iers wiskundige uit de 19e eeuw die zich met zulke problemen bezig hield. In het tweede diagram zie je hoe je alle vlakken precies één keer kunt poetsen. Er zijn nog wel andere perfecte oplossingen, maar er moet ergens gezigzagd worden. Snap je waarom? Het derde diagram toont een oplossing met het minste aantal zigzags. Met wat meer zigzags lukt het zelfs om terug te komen waar je was begonnen (vierde diagram). Dat is een zogenaamde Hamiltoncykel. Als je zelf ook een mooie oplossing hebt gevonden dan wil de familie Van der Torus die graag horen.

Voor het ondergebit werkt hetzelfde diagram (eventueel gespiegeld). Aan de uiteinden zijn de paden langs het bovenen ondergebit aan elkaar te maken door via een voorvlak over te stappen.

Pi hecht minder aan perfectie en dat zigzaggen toch niet zo handig dus volgt het onderste diagram, waarbij de achterkant van de tanden dubbel worden gepoetst (wat niet eens zo'n slecht idee is omdat daar, zeker bij het ondergebit, makkelijker tandsteen ontstaat). Heb je gezien dat Pi ook smokkelt door van een kauwvlak van een kies naar het achtervlak van een hoektand te springen en omgekeerd (de twee rode lijntjes)?