Oplossing Pythagoras Olympiade 62-1
Opgave 481 [oOO]
Omdat getallen niet met een nul beginnen, zullen we de berekening in twee gevallen opdelen.
Eerst tellen we de getallen die bestaan uit enkel nullen en één ander cijfer. Dit andere cijfer moet vooraan staan; hiervoor zijn $9$ mogelijkheden. Gegeven dit cijfer, zijn er precies $7$ manieren waarop we de laatste drie cijfers kunnen invullen; we hebben namelijk per cijfer twee keuzes,, dus $2^3 = 8$ in totaal, maar de optie waarbij we nergens een nul kiezen is niet toegestaan. Dit levert in totaal $9 \cdot 7 = 63$ mogelijke getallen.
Nu tellen we de getallen waarin geen nul voorkomt. We hebben $9 \cdot 8 / 2 = 36$ mogelijkheden om de twee cijfers waaruit ons getal bestaat te kiezen. Ditmaal hebben we 14 mogelijkheden om het getal met deze cijfers in te vullen; we hebben namelijk opnieuw per cijfer 2 keuzes, dus $2^4 = 16$ in totaal, maar de opties waarbij alle getallen hetzelfde zijn, moeten we uitsluiten. Dit levert in totaal $36 \cdot 14 = 504$ mogelijke getallen.
Deze twee gevallen samengenomen levert $504 + 63 = 567$ mogelijkheden.
Opgave 482 [oOO]
Veronderstel dat $n$ van de vorm $5k+4$ is. Dan berekenen we dat
$$6n + 1 = 6(5k+4) + 1 = 30k + 25 = 5(6k+5)$$
een veelvoud is van $5$, en in het bijzonder voor $k > 0$ niet priem. Omdat elk vijfde getal van de vorm $5k+4$ is, volgt zo dat er nooit meer dan vier opeenvolgende getallen in de rij priem kunnen zijn. Anderzijds geldt dat
$$6 \cdot 10 + 1 = 61, \quad 6 \cdot 11 + 1 = 67, \quad 6 \cdot 12 + 1 = 73 \quad \text{en} \quad 6 \cdot 13 + 1 = 79$$
allevier priem zijn. We concluderen dus dat vier opeenvolgende priemgetallen maximaal is.
Opgave 483 [ooO]
We tellen het aantal drietallen waarvan het gemiddelde gelijk is aan één van de drie getallen. Hiertoe merken we op dat zo'n drietal volledig vastligt door het grootste en het kleinste getal, daar het gemiddelde immer in het midden zal liggen. We hoeven dus enkel keuzes van twee getallen te tellen waarvoor het gemiddelde geheel is, want dit gemiddelde wordt dan het derde getal van ons drietal.
Hiertoe merken we op dat het gemiddelde van twee even getallen en van twee oneven getallen geheel is, maar van een even en een oneven getal niet. Omdat $n$ even is, bestaan er precies $n/2$ even getallen tussen 1 en $n$, en precies $n/2$ oneven getallen. Het aantal paren van even getallen is dan gelijk aan
$$\frac{1}{2} \cdot \frac{n}{2} \cdot \left( \frac{n}{2} - 1 \right),$$
en evenzo voor het aantal paren oneven getallen. In totaal vinden we dus
$$\frac{n}{2} \cdot \left( \frac{n}{2} - 1 \right) = \frac{n(n-2)}{4}$$
drietallen waarvan het gemiddelde gelijk is aan een van de drie getallen. In totaal zijn er
$$\frac{n(n-1)(n-2)}{6}$$
mogelijke drietallen. De kans dat we een van de drietallen van hierboven kiezen is dan
$$\frac{6n(n-2)}{4n(n-1)(n-2)} = \frac{3}{2(n-1)}.$$
Opgave 484 [ooO]
We beweren dat zo'n betegeling mogelijk is voor $n = 2$ en voor alle $n \geq 5$. De afbeelding hieronder maakt hiermee een begin.
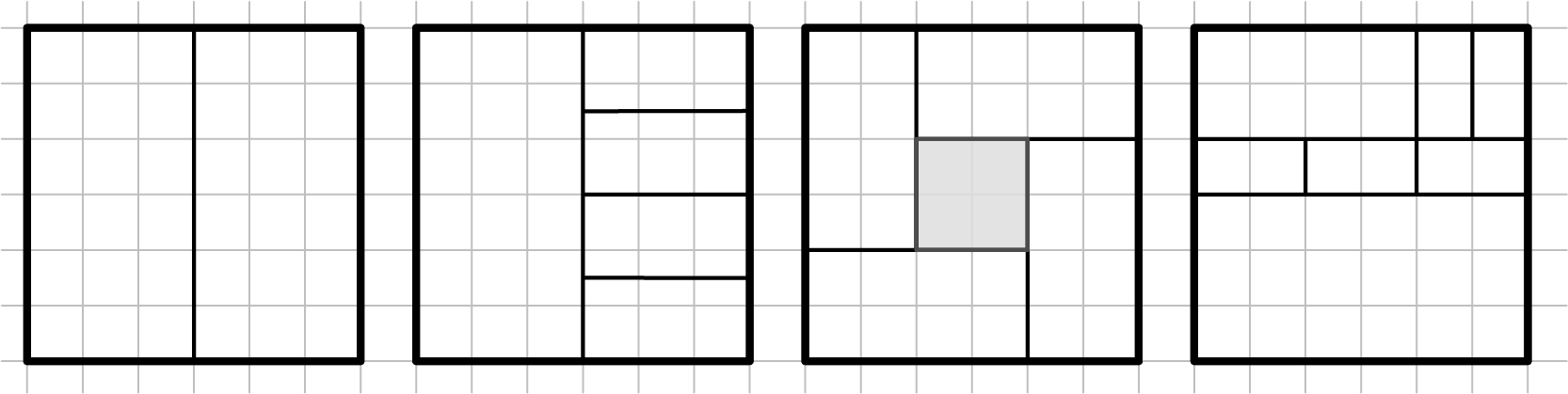
Merk op dat we een $2 \times 1$ rechthoek in vier kleinere $2 \times 1$-rechthoeken kunnen verdelen zoals in de figuur hierboven gedaan is om uit de oplossing voor $n = 2$ de oplossing voor $n = 5$ te construeren. Hieruit volgt dat we, gegeven een oplossing voor $n$ rechthoeken, altijd een oplossing voor $n + 3$ rechthoeken kunnen vinden. Omdat we oplossingen hebben gevonden voor de drie opeenvolgende getallen $n = 5, 6, 7$ volgt hiermee dat we oplossingen voor alle $n \geq 5$ kunnen vinden.
Om de bonus te voltooien, volstaat het dan om te laten zien dat het voor 3 en 4 rechthoeken niet kan. Omdat een vierkant vier hoeken heeft, zou er in het geval van drie rechthoeken een rechthoek moeten zijn die twee hoeken bedekt, en zo het halve vierkant in beslag neemt. Door deze opmerking te herhalen is het echter eenvoudig in te zien dat de overgebleven $2 \times 1$ rechthoek niet in twee $2 \times 1$ rechthoeken kan worden opgedeeld.
Het geval met vier rechthoeken is iets meer werk; met eenzelfde argument als hierboven sluiten we rap uit dat een rechthoek twee hoeken van het vierkant bedekt, dus resteert het geval waarin elke rechthoek precies 1 hoek van het vierkant bedekt. Een vierkantszijde kan niet door twee korte rechthoekszijdes bedekt worden, want dan zouden deze rechthoeken beide precies de halve grootte van het vierkant moeten zijn. Een rechthoek die met de lange zijde langs een vierkantszijde ligt, reikt niet verder dan halverwege het vierkant. Als een vierkantszijde dan bedekt wordt door twee lange rechthoekszijdes, moeten de twee andere rechthoeken de overstaande zijde dus wel met de korte zijde bedekken, maar dit was niet mogelijk. We concluderen dus dat elke rechthoekszijde door een korte en een lange zijde bedekt moet worden. Echter, als we de afmetingen van de rechthoeken $2a_i \times a_i$ noemen voor $i = 1, 2, 3, 4$, dan volgen vier vergelijkingen $2a_i + a_{i+1} = 1$. De unieke oplossing hiervan is $a_i = 1/3$ voor alle $i$, maar dit levert het geval van $n = 6$ in de afbeelding hierboven; dus niet met 4 rechthoeken.
