Als elke kandidaat op goed geluk twee autootjes pakt, lopen ze uiteraard een groot risico dat er paren zijn die geen gemeenschappelijke auto hebben. Als het publiek vervolgens zo’n paar kiest, gaan ze met lege handen naar huis. Hoe kunnen ze dat voorkomen? Door op een slimme manier af te spreken wie welke autootjes moet pakken.

Er zijn drie Audi’s in het spel. Het zou natuurlijk erg dom zijn als er een kandidaat is die twee Audi’s bezit, of zelfs alle drie. De kandidaten zullen er in elk geval voor zorgen dat dát niet gebeurt. We kunnen dus aannemen dat de drie Audi’s onder drie verschillende kandidaten worden verdeeld. Die drie kandidaten hebben dus ten minste één auto gemeenschappelijk (namelijk de Audi). De Audi zorgt ervoor dat er drie autokoppels ontstaan, waarbij een 'autokoppel' is gedefinieerd als een kandidatenpaar met minstens één gemeenschappelijke auto. Zijn $a$, $b$ en $c$ de drie Audi-bezitters, dan zijn $ab$, $ac$ en $bc$ drie autokoppels.

Elk van de overige zes automerken zorgt eveneens voor drie autokoppels. Dat betekent dat er in totaal maximaal $7 \times 3 = 21$ autokoppels zijn. Het volstaat als een autokoppel precies één gemeenschappelijke auto heeft. Het is niet nodig dat twee Audi-bezitters ook nog eens beiden een Bentley hebben. Als elk autokoppel precies één auto gemeenschappelijk heeft, zijn er precies $21$ autokoppels. Als er autokoppels zijn die meer dan één auto gemeenschappelijk hebben, zijn er minder dan $21$ autokoppels.

Hoeveel kandidatenparen zijn er mogelijk? Dat zijn er $(7 \times 6)/2 = 21$. Hé, precies evenveel als het aantal autokoppels, mits er geen autokoppels zijn met meer dan één gemeenschappelijke auto. Het is daarom zaak de auto’s zó te verdelen, dat elk tweetal kandidaten precies één auto gemeenschappelijk heeft. Dan is immers elk kandidatenpaar een autokoppel en is winst gegarandeerd, ongeacht de vijf keuzes die het publiek zal maken. Als er een autokoppel is dat twee gemeenschappelijke auto’s heeft, dan is er een ánder kandidatenpaar dat beslist geen gemeenschappelijke auto heeft, en lopen de kandidaten het risico te verliezen.

Gelukkig is een van de zeven kandidaten een wiskundige. Hij kent het Fanovlak, genoemd naar de Italiaanse wiskundige Gino Fano, een pionier op het gebied van de 'eindige projectieve meetkunde'. 

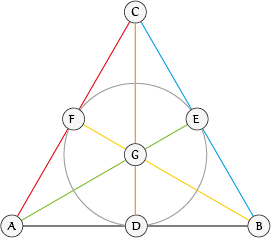
In figuur 1 zie je het Fanovlak. Het bestaat uit zeven punten ($A$ tot en met $G$) en zeven lijnen. Ook de cirkel, die door $D$, $E$ en $F$ gaat, telt als lijn: in de 'eindige projectieve meetkunde' hoeven lijnen niet 'recht' te zijn. Elk punt van het Fanovlak correspondeert met een auto ($A$ = Audi, $B$ =  Bentley enzovoorts.) Elk van de zeven lijnen correspondeert met een kandidaat.

De 'eindige projectieve meetkunde' voldoet aan een aantal eigenschappen waar de gewone, euclidische meetkunde niet aan voldoet, zoals: 'elk tweetal punten bepaalt één lijn die door beide punten gaat' en 'elk tweetal lijnen bepaalt één punt dat op beide lijnen ligt'. Inderdaad voldoet het Fanovlak aan deze twee eigenschappen. Nadat de presentator de eerste zeven auto's heeft verdeeld onder de zeven kandidaten, spreken ze – het Fanovlak in gedachten houdend – het volgende af:

• De kandidaat met een Audi pakt een Bentley en een Daihatsu ($\color{Black}{zwarte}$ lijn).
• Degene met een Bentley pakt een Citroën en een Eagle ($\color{Blue}{blauwe}$ lijn). 
• Degene met een Citroën pakt een Audi en een Ferrari ($\color{Red}{rode}$ lijn).
• Degene met een Daihatsu pakt een Citroën en een Gillet ($\color{Orange}{oranje}$ lijn).
• Degene met een Eagle pakt een Audi en een Gillet ($\color{Green}{groene}$ lijn).
• Degene met een Ferrari pakt een Daihatsu en een Eagle ($\color{Grey}{grijze}$ lijn).
• Degene met een Gillet pakt een Bentley en een Ferrari ($\color{Yellow}{gele}$ lijn).

Welk kandidatenpaar je nu ook kiest, die twee hebben gegarandeerd één auto gemeenschappelijk. Dat komt doordat elke lijn door drie punten gaat en bovendien elk punt op drie lijnen ligt. Al mocht het publiek tien paren aanwijzen, of zelfs alle 21, het maakt niet uit. De hoofdprijs is binnen.

Algemener

Bestaat er ook een oplossing als er niet zeven, maar acht kandidaten en acht automerken – met van elk drie speelgoedmodellen – zijn? Er zijn dan hooguit $8 \times 3 = 24$ autokoppels, terwijl er $(8 \times 7)/2 = 28$ kandidatenparen zijn. Dat gaat dus niet op: er zullen hoe dan ook vier paren zijn die geen enkele auto gemeenschappelijk hebben. Het blijkt dat als $n$ een priemgetal is, of een macht van een priemgetal, er een oplossing bestaat als er $n^2 + n + 1$ kandidaten en $n^2 + n + 1$ automerken zijn, en per merk $n + 1$ speelgoedmodellen. Voor $n = 2$ krijg je het geval dat we hebben besproken.

Voor $n = 3$ hebben we de situatie met $13$ kandidaten en $13$ automerken, van elk merk vier speelgoedmodellen. Als $a$, $b$, $c$ en $d$ de vier Audi-bezitters zijn, dan zijn $ab$, $ac$, $ad$, $bc$, $bd$ en $cd$ zes autokoppels. Omdat er $13$ automerken zijn, zijn er in totaal dus (maximaal) $13 \times 6 = 78$ autokoppels. Dat is precies zo veel als het aantal kandidatenparen: $(13 \times 12)/2 = 78$.

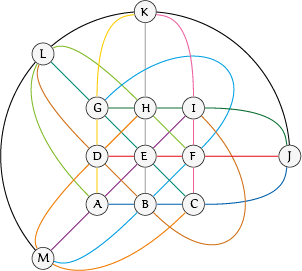
In figuur 2 zie je het equivalent van het Fanovlak voor $13$ punten en $13$ lijnen. Elk punt correspondeert met een auto en elke lijn met een kandidaat (voor de duidelijkheid zijn de lijnen met verschillende kleuren weergegeven). Opnieuw wordt voldaan aan de volgende belangrijke eigenschappen: 'elk tweetal punten bepaalt één lijn die door beide punten gaat’ en ‘elk tweetal lijnen bepaalt één punt dat op beide lijnen ligt’. Daardoor lukt het de 13 kandidaten een verdeling te maken zodat elk kandidatenpaar precies één auto gemeenschappelijk heeft. Voor $n = 4$ bestaat er ook een oplossing, want $4$ is een macht van het priemgetal $2$. Ook voor $n = 5$ (priem) is er een oplossing. Maar voor $n = 6 = 2 \times 3$ niet. Voor $n = 7$, voor $n = 8 = 2^3$ en voor $n = 9 = 3^2$ weer wel, maar voor $n = 10 = 2 \times 5$ dan weer niet. Dit laatste werd in 1988 bewezen – een grote doorbraak die zonder computer niet mogelijk was geweest.

En hoe zit het voor $n = 12 = 2^2 \times 3$? Dat weet niemand. Het is een open probleem in de wiskunde of er vlakken à la het Fanovlak bestaan als $n$ groter is dan $10$ en ten minste twee verschillende priemdelers heeft.

 

		Onlangs is het boek The Raven's Hat verschenen, geschreven door Jonas Peters en Nicolai Meinshausen. Het boek bevat acht hoofdstukken. In elk hoofdstuk beschrijven Peters en Meinshausen een wiskundig probleem waarvan je in eerste instantie denkt: huh, kan dat wel? Over sommige van die problemen hebben we al eerder geschreven in Pythagoras.  Bijvoorbeeld over het kluisjesprobleem, in Pythagoras 46-6 (juni 2007), of over het ophangen van een schilderij aan een stel spijkers, in Pythagoras 50-5 (april 2011).  Het probleem dat we in dit artikel bespreken, komt uit hoofdstuk 6 van The Raven’s Hat. De wiskunde in dit boek gaat vaak verder dan wat je op de middelbare school leert. Maar de problemen zijn stuk voor stuk erg leuk, dus het loont om je even schrap te zetten!