Opgave 1

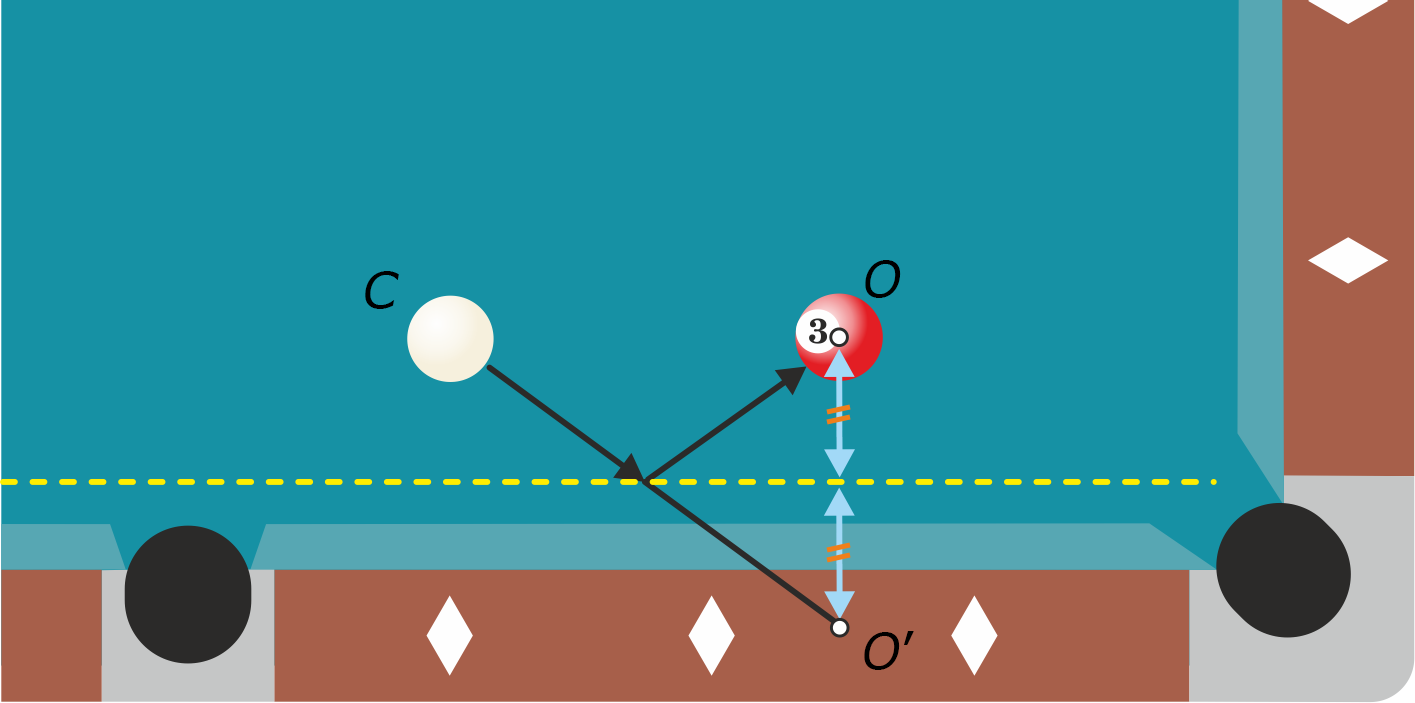
Opgave 2

Hiervoor heb je het spiegelbeeld $C’$ van $C$ in band 1 en het spiegelbeeld $G’$ van $G$ in band 2 nodig.

Zie de figuur.

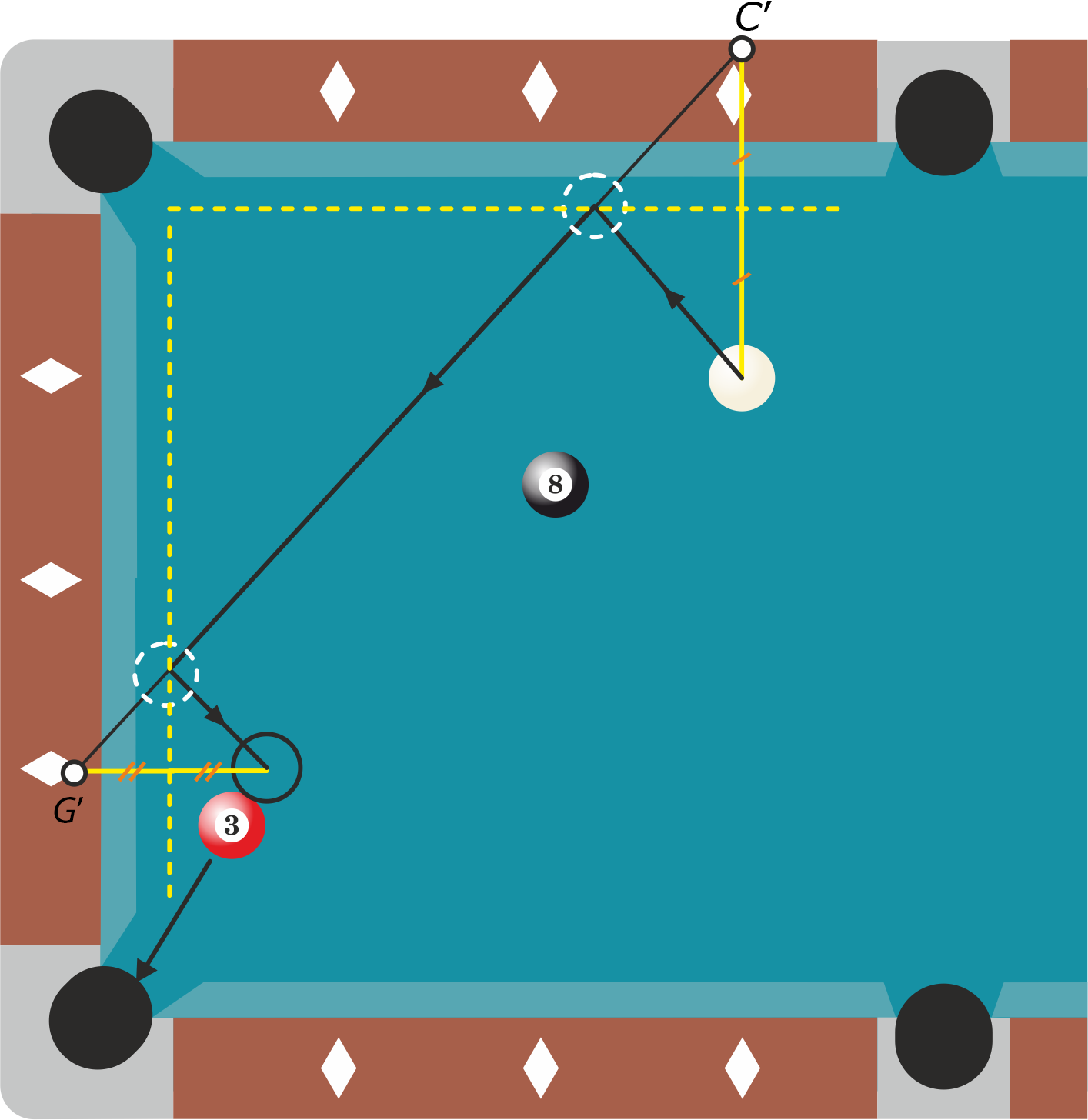
Opgave 3

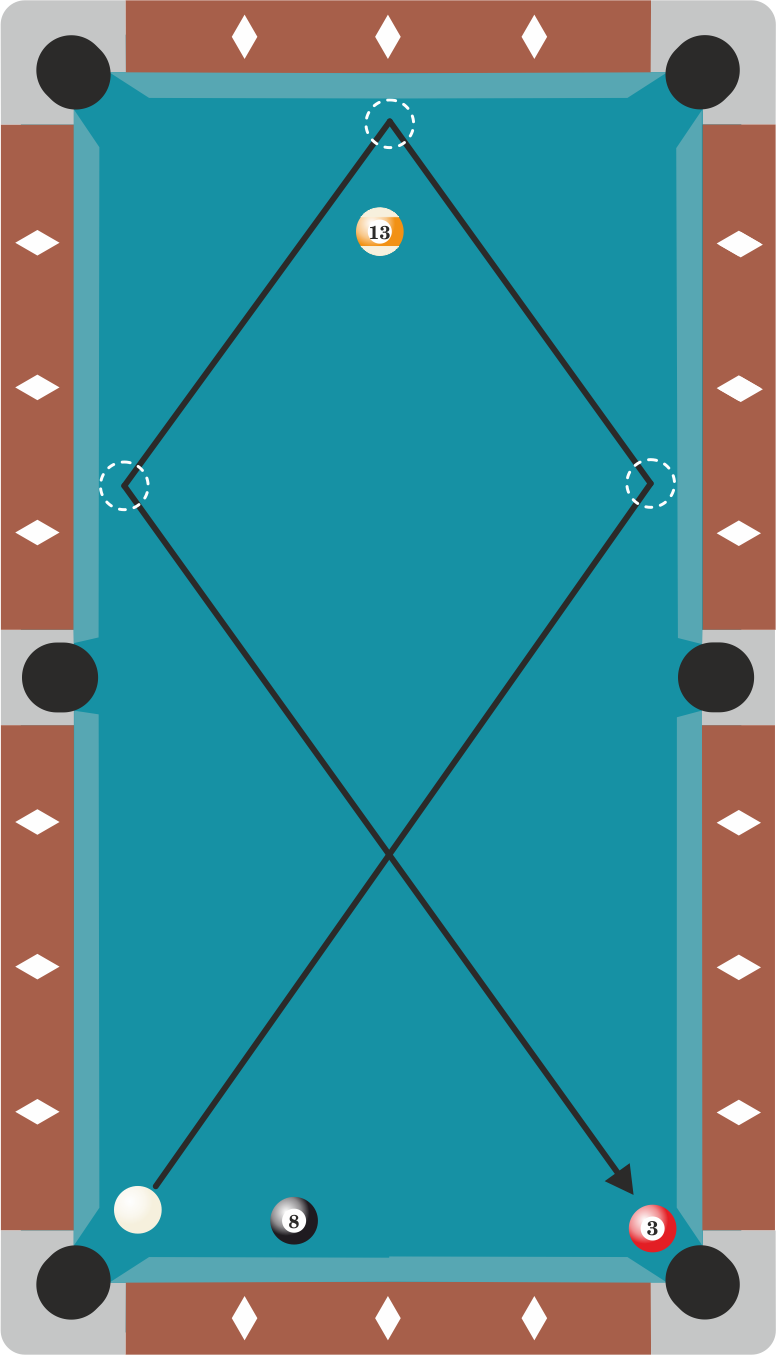
Opgave 4

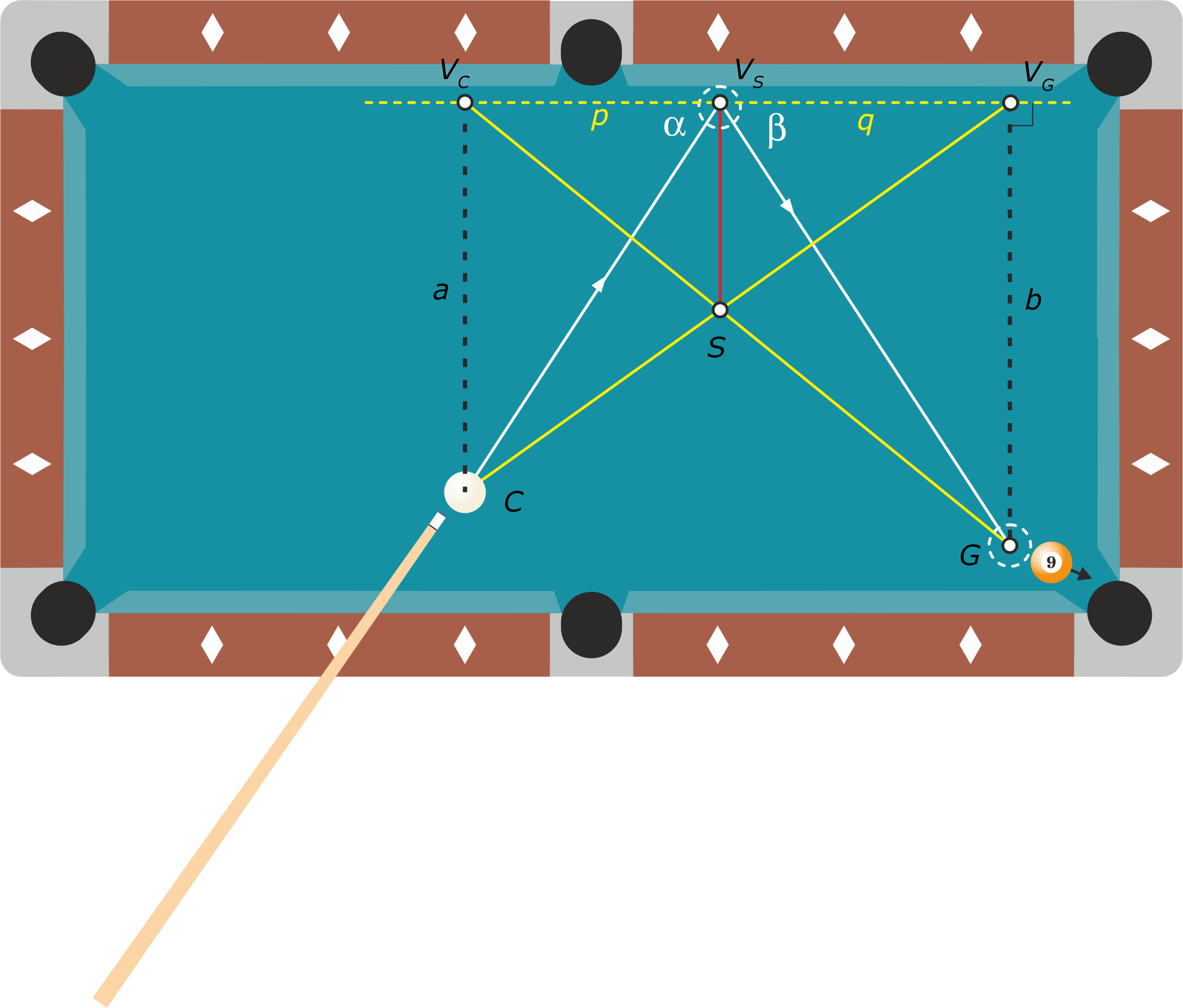
In de figuur zijn de driehoeken $CV_CS$ en $ V_GGS$ gelijkvormig.

Omdat $p$ en $q$ even lang zijn als de hoogtelijnen van die twee driehoeken, volgt daaruit dat de driehoeken $CV_CV_S$ en $GV_GV_S$ ook gelijkvormig zijn. Daarom zijn de hoeken $\alpha$ en $\beta$ gelijk aan elkaar en loopt de cue ball via punt $V_S$ naar de ghost ball.

Opgave 5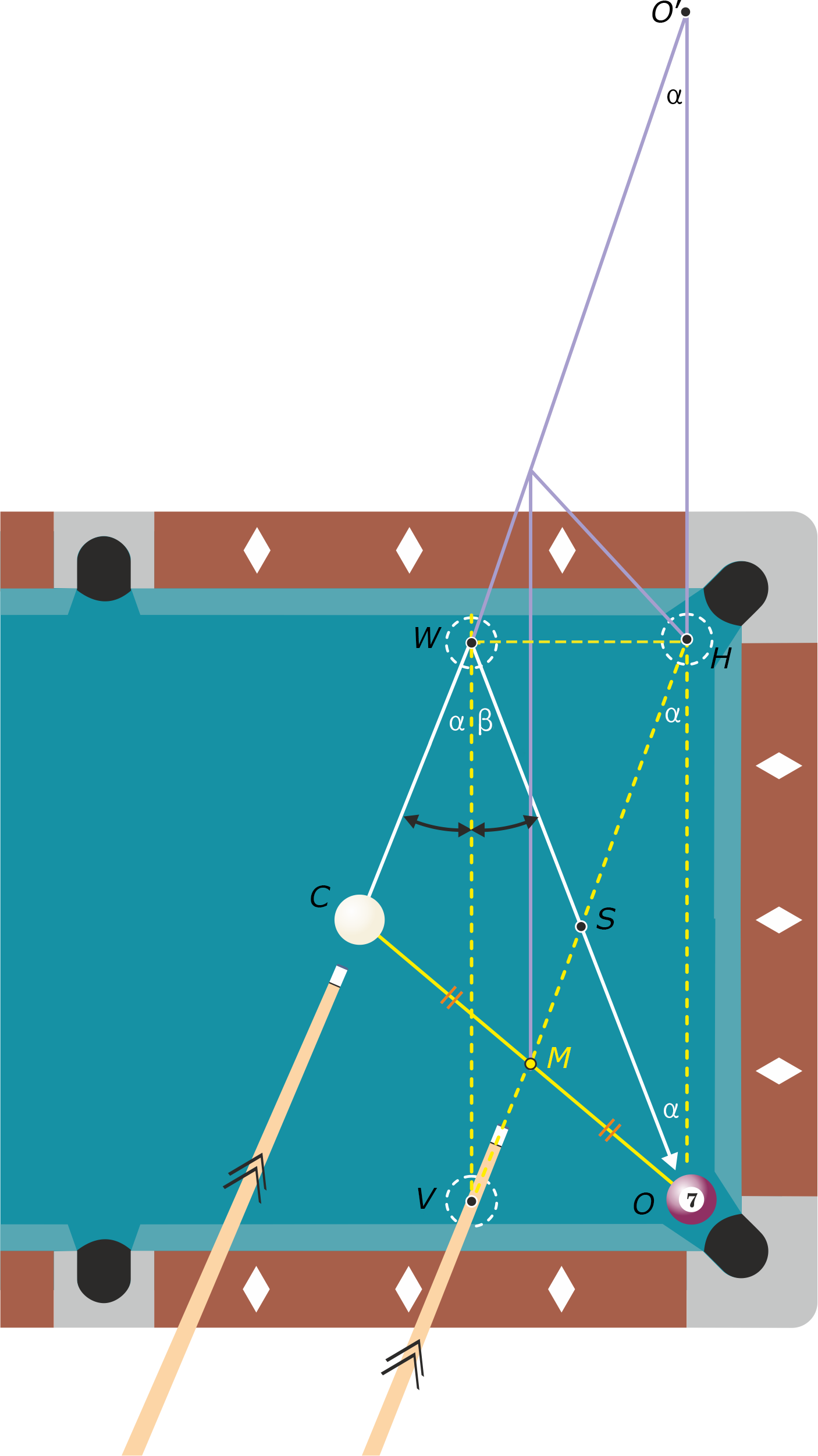

 

 

 

 

 

Te bewijzen: in de figuur geldt hoek $\alpha$ = hoek $\beta$.

Lijn $MH$ loopt evenwijdig aan lijn $CW$ (omdat we dat zo gekozen hebben). Het snijpunt van lijn $CW$ met lijn $HO$ noemen we $O'.$ De lijn $WV$, loodrecht op de band, is evenwijdig met $HO.$ Dus is hoek $\alpha$ een F-hoek met hoek $O’.$ Dus hoek $O’$ is ook gelijk aan $\alpha.$ Driehoek $MOH$ is gelijkvormig met driehoek $COO'$, met vergrotingsfactor 2 (want $CO$ = $2MO,$ door de keuze van $M$). Dus geldt $HO = HO'.$ Ook geldt $O'$ is het spiegelpunt van $O$ in lijn $HW$. Dan is driehoek $OWO'$ gelijkbenig, met basishoeken $\alpha.$ Hoek $O$ in driehoek $WHO$ is ook $\alpha,$ en die is een Z-hoek met hoek $\beta.$ Daaruit volgt dat hoek $\alpha$ = hoek $\beta.$

Dus de teruggekaatste cue ball volgt lijn $WO.$