Opgave 1

De aardas

Opgave 2

$\angle L_{12} = \angle LKM=90^{\rm o}$ (Z-hoeken)

$\angle L_{23} = 90^{\rm o}$ (een raaklijn aan de cirkel staat loodrecht op de straal)

$\angle L_3=\angle M=52^{\rm o}$ (Z-hoeken)

We kunnen nu uitekenen:

$\angle L_2=90^{\rm o} - \angle L_3=90^{\rm o}-52^{\rm o}=38^{\rm o}$

$\angle L_1=90^{\rm o}- \angle L_2=90^{\rm o}-38^{\rm o}=52^{\rm o}$

Opgave 3

Horizontaal

Opgave 4

Verticaal

Opgave 5

De evenaar (equator)

Opgave 6

$180^{\rm o}/12=15^{\rm o}$

Opgave 7

$360^{\rm o}/24=15^{\rm o}$

Opgave 8

De poolster (Polaris, $\alpha$ Ursae Minoris)

Opgave 9

$38^{\rm o}$

(Stap 3)

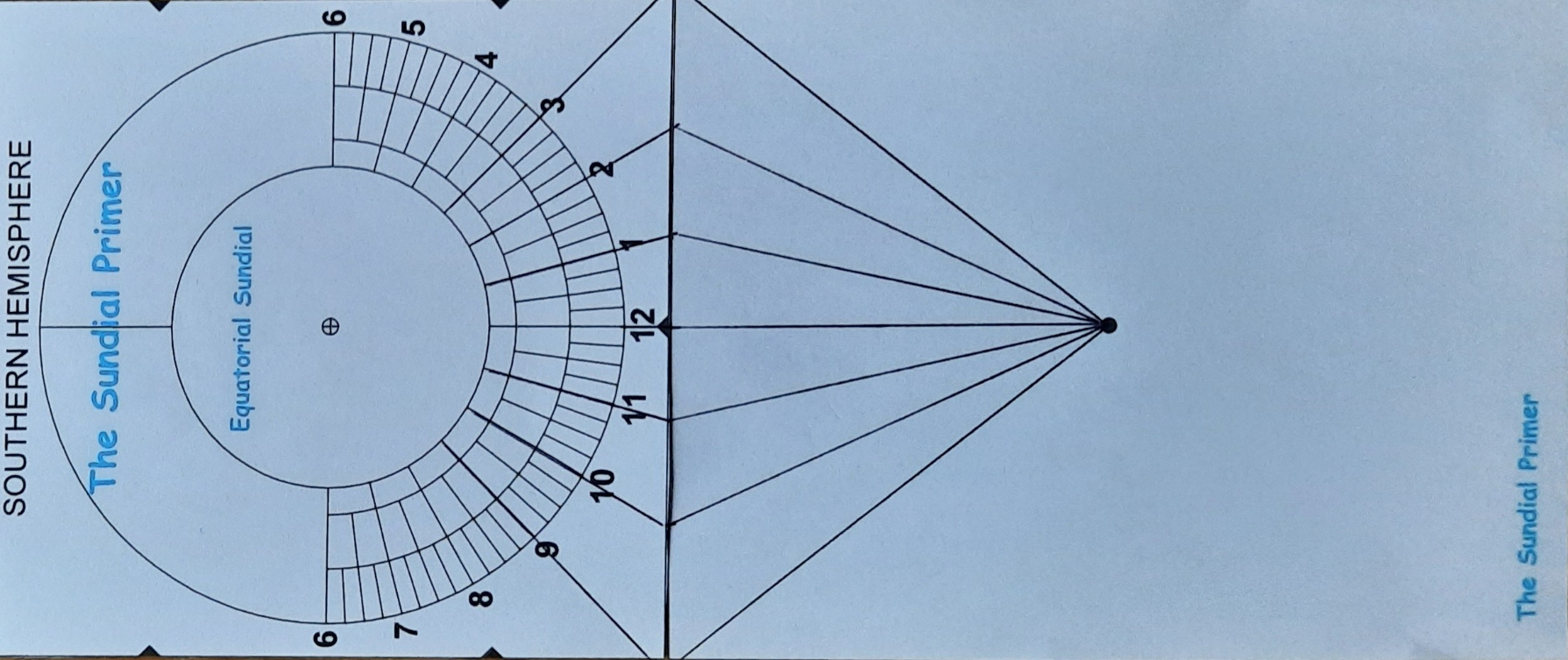
Opgave 10

In tegenstelling tot de uurhoeken van de equatoriale zonnewijzer zijn die de uurhoeken van een horizontale zonnewijzer niet allemaal even groot.

Opgave 11

De stip dichter bij de raaklijn tekenen betekent een hogere breedtegraad.

De hoeken tussen 12 en 1 uur, 1 en 2 uur en 2 en 3 uur worden groter. Omdat alle uurhoeken tussen 06:00 en 12:00 samen $90^{\rm o}$ moeten zijn, kan dit niet voor alle uurhoeken gelden.

Opgave 12

De stip verder van de raaklijn vandaan tekenen betekent een lagere breedtegraad.

De hoeken tussen 12 en 1 uur, 1 en 2 uur en 2 en 3 uur worden kleiner. Omdat alle uurhoeken tussen 06:00 en 12:00 samen $90^{\rm o}$ moeten zijn, kan dit niet voor alle uurhoeken gelden.

(Stap 5)