1.	Het vierkant is voor de helft ingekleurd.
2.	Verdeel het vierkant in negen gelijke vierkanten. Elk vierkant heeft de oppervlakte van een 1/9. Het vierkant in het midden is volledig gevuld, vier vierkanten zijn voor de helft gevuld (zie 1). In totaal zijn ingevuld:  $\frac19 + 4 \times \frac12 \times \frac19 = \frac19 + 2 \times \frac19 = \frac39 = \frac13$.  Het vierkant is dus voor $\frac13$ ingekleurd.
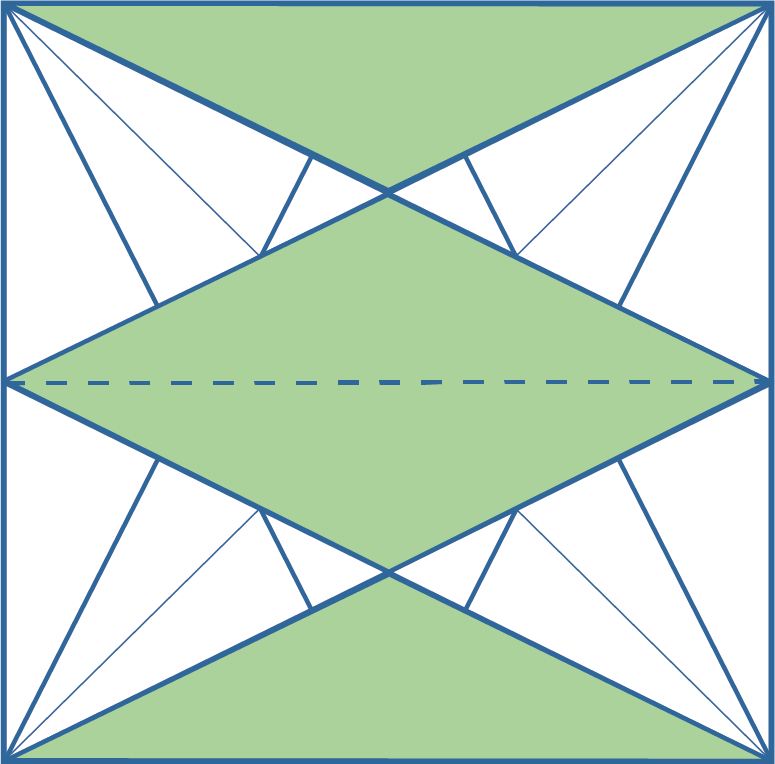
3.	Je kunt nog drie van dezelfde driehoeken in het vierkant inkleuren. De helft van het vierkant is dan bedekt.  De oplossing is dus $\frac14 \times \frac12 = \frac18$.
4.	In het plaatje zie je dat een driehoek en een vijfhoek samen precies weer één vierkant vormen. In totaal kun je dan nog vier vierkanten in het grote vierkant kwijt.  In totaal is het vierkant zo in vijf gelijke oppervlakten in te delen. Het ingekleurde vierkant in het midden heeft dus een oppervlakte van $\frac15$.
5.	We zien dat de twee driehoeken precies de helft van het vierkant (zie 4) in het midden bedekken. Net als bij 1. deel je het vierkant zo in twee delen.  Een vierkant in het midden is $\frac15$ (zie 4). Twee driehoeken zijn de helft daarvan:  $\frac12 \times \frac15 = \frac{1}{10}$.
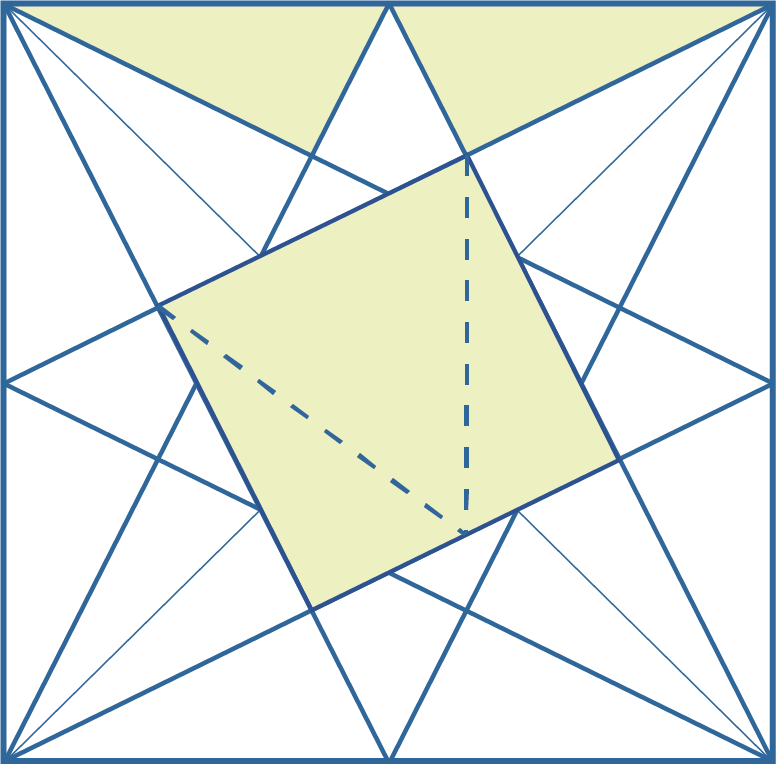
6.	Om de oppervlakte van deze vlieger te berekenen, kleuren we eerst de andere drie punten in. Met de oplossingen van 2 en 5 kun je hele vierkant volleggen.  En nu rekenen maar: De ster: $\frac13$ (zie 2). $4$ setjes gele driehoeken (zie 5): $4 \times \frac{1}{10} = \frac{4}{10} = \frac25$.  Bij elkaar is dit: $\frac13 + \frac25 = \frac{5}{15} + \frac{6}{15} = \frac{11}{15}$.  Voor de vier vliegers blijft dus over:  $1 - \frac{11}{15} = \frac{15}{15} - \frac{11}{15} = \frac{4}{15}$.  $1$ vlieger is dus $\frac{1}{15}$.
7.	Je vult het vierhoekje aan met de twee driehoeken (zie 5.). De aldus ontstane nieuwe driehoek is even groot als een groene driehoek die we al hadden berekend bij opdracht 3 (antwoord $\frac18$). En dus geldt voor de oppervlakte van de blauwe vierhoek:  Grote driehoek – twee kleine driehoeken:  $\frac18 - \frac{1}{10} = \frac{5}{40} - \frac{4}{40} = \frac{1}{40}$.  De vierhoek heeft een oppervlakte van $\frac{1}{40}$.
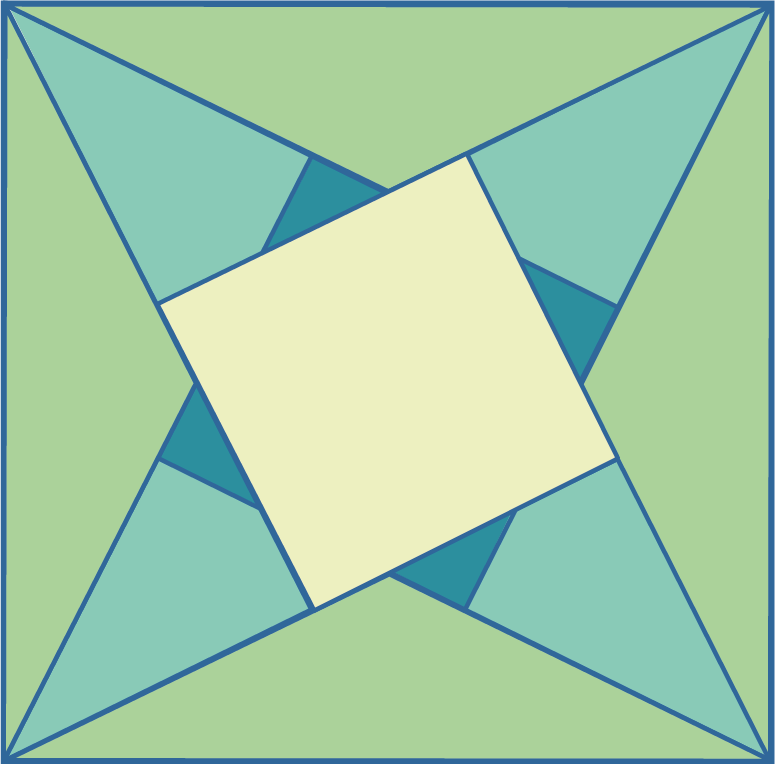
8.	Om de oppervlakte van de vier kleine driehoeken uit te rekenen leg je het hele vierkant vol met het vierkant (zie 4), vier vliegers (zie 6) en vier driehoeken (zie 3). Bij elkaar is dat:  $\frac15 + 4 \times \frac{1}{15} + 4 \times\frac18 = \frac15 + \frac{4}{15} + \frac12 =$  $\frac{6}{30} + \frac{8}{30} + \frac{15}{30} = \frac{29}{30}$.  Voor de vier kleine driehoekjes blijft dus over:  $1 - \frac{29}{30} = \frac{30}{30} - \frac{29}{30} = \frac{1}{30}$.  En één zo’n driehoekje heeft dus een oppervlakte van $\frac{1}{120}$.
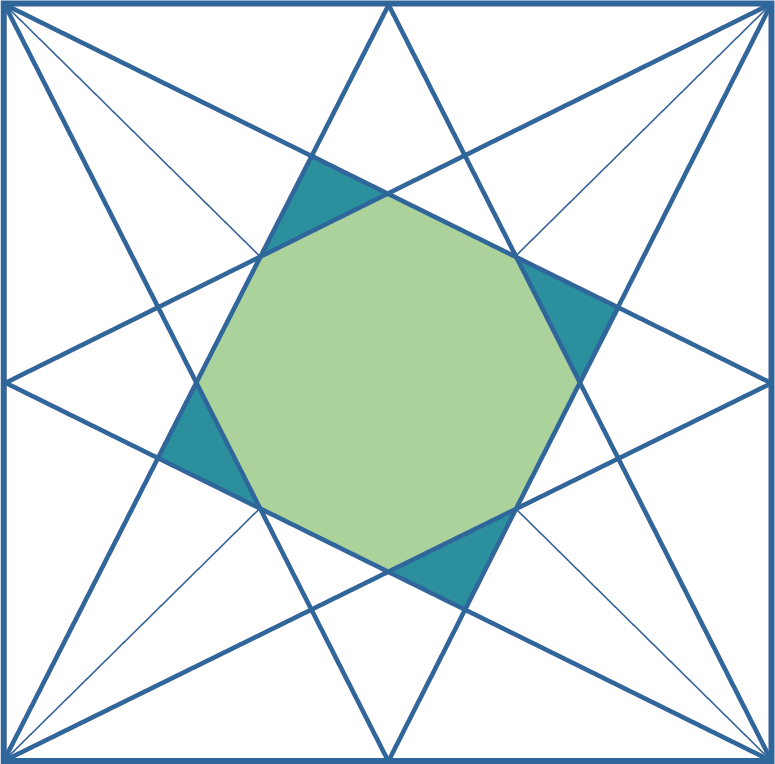
9.	Voor de oplossing van dit raadsel heb je de oplossing van de raadsels 4 en 8 nodig: de achthoek vormt samen met de vier driehoekjes (zie 8) een vierkant (zie 4). Er geldt: $\mbox{achthoek + vier driehoekjes}$ $=$ $vierkant$ $achthoek + \frac{1}{30}$ $=$ $\frac15=\frac{6}{30}$ De oppervlakte van de achthoek is dus gelijk aan $\frac{5}{30} = \frac16$.