Oplossingen Kleine Nootjes 59-4
Mooie wiskunde in 2020
Een oplossing is: $1+1+2+2\times 3\times3\times4+4+5\times5\times6\times6+7\times7\times8+8\times9\times9=2020$.
Kleiner dan 1?
Er geldt $a < 1$ en dus ook $a < (1 - b)/(1 - b)$. Links en rechts vermenigvuldigen met de positieve $1 - b$ en uitwerken levert $a + b - ab < 1$.
Twee gelijkbenige driehoek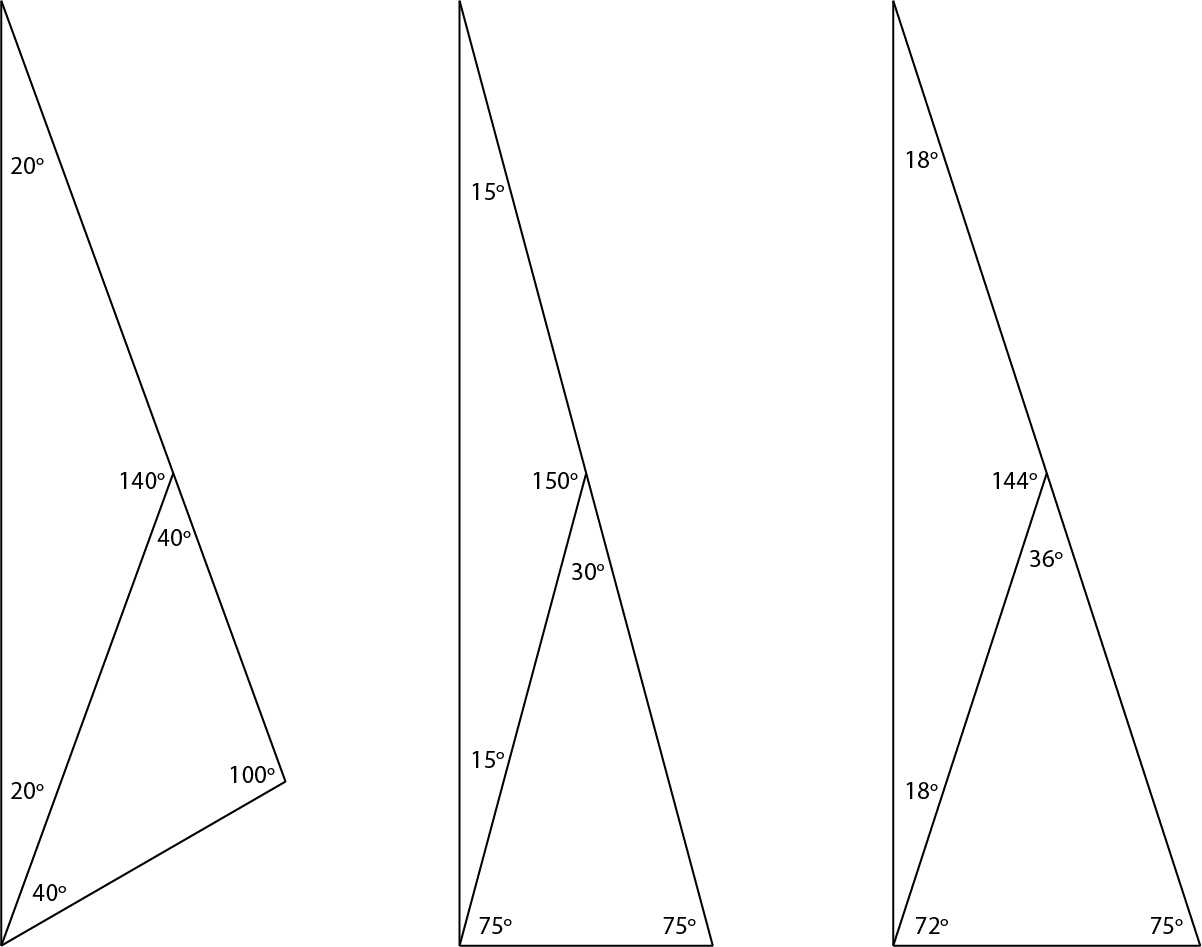 en
en
Er zijn drie oplossingen. Zie de figuur.
Dobbelsteenvariaties
De $1$ kun je altijd boven zetten.
Voor de $2$ heb je dan 2 mogelijkheden:
- Mogelijkheid 1: tegenover de $1$.
- De $3$ kun je dan zetten waar je wilt.
- Met $4$, $5$ en $6$ levert vervolgens elke volgorde op de overige 3 zijvlakken een verschillende dobbelsteen.
- Mogelijkheid : naast de $1$.
- Voor de $3$ heb je dan vier mogelijkheden, die steeds tot verschillende dobbelstenen leiden.
- In elk van deze 4 gevallen zijn er weer 6 mogelijkheden voor de getallen $4$, $5$ en $6$.
In totaal zijn er dus $5 \times 6 = 30$ verschillende dobbelstenen mogelijk.
Een, twee of drie soorten gewichtjes?
Er zijn drie wegingen nodig. Noem de balletjes p, q en r. De wegingen Ia, Ib, IIa, enz.
- Ia) p = q
- IIa) p = r → 1 soort
- IIb) p > r → 2 soorten
- IIc) p < r → 2 soorten
- Ib) p > q
- IIa) p = r → 2 soorten
- IIb) p < r → 3 soorten
- IIc) p > r
- IIIa) q = r → 2 soorten
- IIIb) q > r → 3 soorten
- IIIc) q < r → 3 soorten
- Ic) p < q
- IIa) q = r → 2 soorten
- IIb) q < r → 3 soorten
- IIc) q > r
- IIIa) p = r → 2 soorten
- IIIb) p < r → 3 soorten
- IIIc) p > r → 3 soorten
