Oplossing 338 [niveau oOO]

Een mier loopt over de blauwe paden. Hij start in punt $A$ en wil via $B$ naar $C$ komen. Langs welke andere punten $D$, $E$ en $F$ komt de mier nog meer, als hij de kortst mogelijke weg kiest? De stralen van de binnenring en buitenring verhouden zich als $2 : 3$.

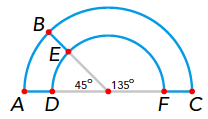
Oplossing. Stel dat de binnenring straal $2$ heeft en de buitenring straal $3$. De mier kan ofwel van $A$ via $B$ naar $C$ lopen (geheel over de buitenring), ofwel van $A$ via $B, E$ en $F$ naar $C$ (eerst over de buitenring, dan over de binnenring). De omtrek van een cirkel met straal $r$ is gelijk aan $2\pi r$.
De eerste route heeft een lengte van ${1 \over 2} · 2\pi · 3 ≈ 9,42$. De tweede route heeft een lengte van ${45 \over 360} · 2π · 3 + 1 + {135 \over 360} · 2π · 2 + 1 ≈ 9,07$.
De tweede route is dus korter.

 

Oplossing 339 [niveau oOO]

Vereenvoudig zo ver mogelijk:
\({1 \over \sqrt2 + \sqrt3} + {1 \over \sqrt3+\sqrt4} + ... + {1 \over \sqrt {199} + \sqrt{200}}\)
Oplossing. Gebruikmakend van het feit dat
\({1 \over \sqrt{n} + \sqrt{n+1}} = {\sqrt{n+1}-\sqrt{n} \over (\sqrt{n+1} - \sqrt{n})(\sqrt{n}+\sqrt{n+1})} = \sqrt{n+1}-\sqrt{n}\)
vinden we:\begin{eqnaray*}

 

Oplossing 340 [niveau ooO]

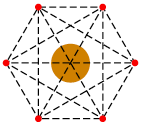Zes kinderen schoppen een balletje over. Iedereen speelt de bal met gelijke kans over aan elk ander, maar natuurlijk nooit aan zichzelf. (Dus de kans dat $A$ de bal naar $B$ overspeelt, is ${1 \over 5}$ , en idem voor de kans dat $A$ de bal naar $C, D, E$ of $F$ overspeelt.) In het midden van het veld ligt een modderplas. Zodra de bal hier ook maar één keer doorheen gaat, dan is de bal de rest van het potje vies. Na zes keer overspelen is iedereen het zat (ook als er eventueel mensen zijn die de bal nooit gekregen hebben). Wat is de kans dat de bal nog schoon is?
Oplossing. Iedere speler kan de bal naar 5 medespelers overspelen. Eén speler van deze 5 staat pal tegenover de speler die aan zet is. Het spelen van de bal naar deze speler veroorzaakt een vieze bal. Als de bal naar één van de andere 4 spelers wordt gespeeld, blijft de bal schoon. De kans dat de bal zes keer achter elkaar niet door het midden wordt gespeeld, is dus (${4 \over 5}$)⁶ ≈ 0,26.

 

Oplossing 341 [niveau ooO]

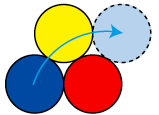
Een gele, een blauwe en een rode schijf liggen zoals getekend in de figuur. Je mag steeds één van de drie schijven over de andere twee heen tillen en er aan de andere kant weer tegenaan zetten. (In de figuur zie je hoe je de blauwe schijf kunt verplaatsen.) Is het mogelijk om op deze manier de schijven op precies dezelfde plek te krijgen als waar we begonnen waren, maar dan met twee of meer kleuren omgewisseld?
Oplossing.  Bekijk waar de schijven terecht kunnen komen. In de figuur zijn enkele schijven getekend. Het maakt niets uit op welke manier je de schijven ten opzichte van elkaar spiegelt. De kleur van de schijf op een bepaalde plaats is onafhankelijk van de weg naar die plaats toe. Dit geldt in het bijzonder voor de plekken waar de schijven oorspronkelijk liggen. De schijven zullen niet omgewisseld raken.