Oplossing 346 [niveau oOO]

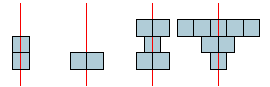
We tekenen torens met vierkantjes. Hieronder zijn alle torens getekend met 2 vierkantjes en er zijn voorbeelden van torens getekend met 5 en 8 vierkantjes. Het recept om een toren te tekenen is als volgt: je tekent eerst een verticale symmetrieas, en vervolgens plaats je per laag een aantal vierkantjes rondom de symmetrieas. Hoeveel torens kun je maken met 3, 4, 5 en 6 vierkantjes?

Oplossing. Het aantal verschillende torens met 3 vierkantjes is 4:

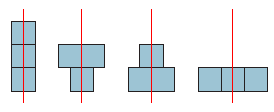
We laten zien hoe je uitgaande van 3 vierkantjes waarmee je 4 verschillende torens kunt bouwen, je met 4 vierkantjes 8 verschillende torens kunt bouwen. Bekijk de volgende 4 torens:

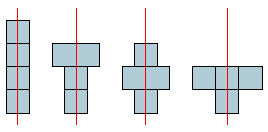
Dit zijn dezelfde torens als de torens die je kunt maken met 3 vierkantjes, behalve dan dat er onderaan een vierkantje is toegevoegd. Bekijk nu de volgende 4 torens:

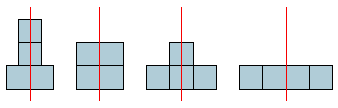
Hier is steeds een vierkantje toegevoegd aan de onderste rij vierkantjes. Dit principe geldt algemeen: uitgaande van een toren met n vierkantjes kun je precies 2 keer zo veel torens maken met n + 1 vierkantjes. Dit bewijsprincipe heet volledige inductie.
Kortom: met 3, 4, 5, 6 vierkantjes kun je achtereenvolgens 4, 8, 16, 32 torens bouwen.

 

Oplossing 347 [niveau oOO]

Wat is het kleinste positieve gehele getal $n$ waarvoor geldt dat ${1 \over 2} n^2$ een derdemacht is en ${1 \over 3} n^3$ een kwadraat?
Oplossing. We herschrijven de opgave tot
\(\begin{eqnarray} n^2 &=& 2a^3,\qquad(1)\\ n^3&=&3b^2.\,\qquad(2) \end{eqnarray}\)
Om het rechterlid van $(1)$ een kwadraat te laten zijn, volgt dat $a = 2c^2$, dus geldt $(3)$ $n = 4c^3$. Om het rechterlid van $(2)$ een derdemacht te laten zijn, volgt dat $b = 3d^3$, dus geldt $(4)$ $n = 3d^2$. Uit $(3)$ en $(4)$ volgt $(5)$ $4c^3 = 3d^2$. Nu volgt dat $c$ een drievoud moet zijn, ofwel $(6)$ $c = 3e$. Substitueren we $(6)$ in $(5)$, dan vinden we $(7)$ $108e^3 = 3d^2$. Nu moet $d$ een zesvoud zijn: $(8)$ $d = 6f$. Substitueren we $(8)$ in $(6)$, dan vinden we $(9)$ $108e^3 = 108f^2$. Nu volgt eenvoudig dat $(10)$ $e = m^2$ en $(11)$ $f = m^3$. We gaan terug naar $(3)$ en maken gebruik van $(6)$ en $(10)$. Dan vinden we $(12)$ $n = 4c^3 = 108e^3 = 108m^6$. Dit geldt voor elke gehele waarde van $m$, in het bijzonder voor $m = 1$. De bijpassende kleinste waarde voor $n$ is $108$.

 

Oplossing 348 [niveau ooO]

Als $a + b + c = 0$ en $a^3 + b^3 + c^3 = 2016$, wat is dan het product $abc$?
Oplossing. Er geldt $c = –a – b$. Dus $c^3 = (–a – b)^3 = –a^3 – 3a^2b – 3ab^2 – b^3$. Dan volgt $2016 = a^3 + b^3 + c^3 = a^3 + b^3 – a^3 – 3a^2b – 3ab^2 – b^3 = –3ab(a + b)3abc$. Conclusie: $abc = 672$.

 

Oplossing 349 [niveau ooO]

In een bepaald Tibetaans klooster wonen 36 monniken. De monniken dragen vier kleuren mutsen: rood, wit, blauw en geel. Ieder van deze monniken valt onder één van de zes ordes die leven in dit klooster. Elk van de zes ordes wordt gekarakteriseerd door het dragen van twee verschillende mutsen (rood-wit), (rood-blauw), (rood-geel), (wit-blauw), (wit-geel) en (blauw-geel). Alle monniken van dezelfde orde dragen dagelijks dezelfde muts. Elke monnik weet dagelijks welke kleur is gekozen. Een toerist bezoekt het klooster vier opeenvolgende dagen en telt de mutsen van de monniken:

dag	rood	wit	blauw	geel
maandag	13	12	11	0
dinsdag	0	7	13	16
woensdag	11	12	0	13
donderdag	7	0	20	9

Uit hoeveel monniken bestaan de zes verschillende ordes?
Oplossing. We geven hier de oplossing van Rein Jansen Groesbeek uit klas 6 van het Stedelijk Gymnasium Utrecht. Voer de volgende zes variabelen in:
$a$ = aantal monniken in de rood-wit orde,
$b$ = aantal monniken in de rood-blauw orde,
$c$ = aantal monniken in de rood-geel orde,
$d$ = aantal monniken in de wit-blauw orde,
$e$ = aantal monniken in de wit-geel orde,
$f$ = aantal monniken in de blauw-geel orde.
Een orde kan in elk geval niet meer monniken hebben dan het maximum van hun twee kleuren op een bepaalde dag. Zo is $a ≤ 7$, want op donderdag is het aantal rode mutsen $7$ en het aantal witte mutsen $0$: de orde moet een van de twee kleuren kiezen. Op dezelfde wijze volgt dus dat $b ≤ 11$, $c ≤ 13$, $d ≤ 12$, $e ≤ 9$ en $f ≤ 11$. Verder kan geen enkele orde $0$ leden hebben: als dat wél het geval zou zijn, dan zouden de twee kleuren van die orde elk alleen samengesteld kunnen worden uit de twee andere ordes. Dit zou betekenen dat de aantallen van die mutsen maar drie positieve waarden kunnen aannemen, waarvan een de som is van de andere twee. Dit zien we echter niet terug in de notities van de toerist: drie van de vier kleuren nemen $3$ verschillende positieve waarden aan in de vier dagen waarbij geen enkele waarde de som is van de andere twee. Kijk nu naar het getal met de kleinste bovengrens, $a$. Op donderdag zouden de $7$ rode mutsen kunnen komen door $a$ alleen, door $a + b$, $a + c$ of $a + b + c$.

• Stel dat $a + b + c = 7$ rood. Op maandag zouden er $13$ rode mutsen moeten zijn, maar dit kan niet, want we hebben maar $3$ ordes die rode mutsen kunnen leveren: tegenspraak.
• Stel dat $a + b = 7$ rood. Dan zou er gelden $c + e = 9$ geel of $c + e + f = 9$ geel op donderdag. Stel dat $c + e = 9$ geel op donderdag. Dan zou op donderdag gelden dat $d + f = 20$ blauw. Dan zou op dinsdag gelden $c + e + f = 16$ geel, dus $f = 7$. Hieruit volgt dus dat $d = 20 – f = 13$, wat in tegenspraak is met $d ≤ 12$. Stel dat $c + e + f = 9$ geel. Dan zou op donderdag gelden dat $d = 20$ blauw, wat in tegenspraak is met $d ≤ 12$. Dus $a + b = 7$ rood leidt tot een tegenspraak.
• Stel dat $a + c = 7$ rood. Dan zou er gelden $e + f = 9$ geel of $e = 9$ geel op donderdag. Stel dat $e + f = 9$ geel. Dan zou op dinsdag gelden $c + e + f = 16$ geel of $c + e = 16$ geel of $c + f = 16$ geel, dus $c ≥ 7$. Hieruit volgt dus dat $c = 7$ en $a = 0$. Maar dat kan niet, want geen enkele orde heeft $0$ leden. Stel dat $e = 9$ geel. Dan zou op dinsdag gelden $c + e + f = 16$ geel of $c + e = 16$ geel, dus $c + f = 7$ of $c = 7$. Uit $c = 7$ volgt $a = 0$: opnieuw een tegenspraak. Als $c + f = 7$ geel, dan zou op dinsdag moeten gelden $b + d = 13$ blauw en dus op diezelfde dag $a = 7$ rood. Uit $a = 7$ volgt $c = 0$: tegenspraak. Conclusie: $a + c = 7$ rood leidt tot een tegenspraak.
• We hebben nu alleen nog de optie over dat $a = 7$ rood op donderdag. Op dinsdag zou dan gelden dat $b + d + f = 13$ blauw of $b + d = 13$ blauw en $c + e + f = 9$ geel of $c + e = 9$ geel. Op donderdag zou dan gelden dat $b + d + f = 20$ blauw of $b + d = 20$ blauw en $c + e + f = 16$ geel of $c + e = 16$ geel. We zien dus dat $f$ het verschil van $7$ maakt tussen beide dagen, dus $f = 7$. Dus $b + d = 13$ en $c + e = 9$. Op woensdag moet gelden dat $c + f = 13$ geel ($c = 6$, $e = 3$) of dat $e + f = 13$ geel ($c = 3$, $e = 6$). Op maandag moet gelden dat $b + f = 11$ blauw ($b = 4$, $d = 9$) of dat $d + f = 11$ blauw ($b = 9$, $d = 4$). Op maandag moet gelden dat $a + b + c = 13$ rood of $a + c = 13$ rood of $b + c = 13$ rood. Dit kan alleen als $c = 6$. Dus $d = 3$. Op woensdag moet gelden dat $a + b + c = 11$ rood of $a + b = 11$ rood of $b + c = 11$ rood. Dit kan alleen als $b = 4$. Dus $d = 9$. We hebben nu de aantallen van de zes ordes achterhaald en bewezen dat dit de enige mogelijke samenstelling is van monniken: $a = 7$, $b = 4$, $c = 6$, $d = 9$, $e = 3$ en $f = 7$. Er is ook maar één mogelijke manier voor de ordes om hun hoeden te kiezen zodat ze die kleurensamenstelling krijgen in die vier dagen.