Opgave 346 [niveau oOO]

We tekenen torens met vierkantjes. Hieronder zijn alle torens getekend met 2 vierkantjes en er zijn voorbeelden van torens getekend met 5 en 8 vierkantjes. Het recept om een toren te tekenen is als volgt: je tekent eerst een verticale symmetrieas, en vervolgens plaats je per laag een aantal vierkantjes rondom de symmetrieas. Hoeveel torens kun je maken met 3, 4, 5 en 6 vierkantjes?

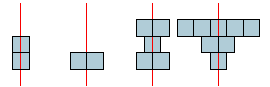
Opgave 347 [niveau oOO]

Wat is het kleinste positieve gehele getal $n$ waarvoor geldt dat ${1 \over 2} n^2$ een derdemacht is en ${1 \over 3} n^3$ een kwadraat?

 

Opgave 348 [niveau ooO]

Als $a + b + c = 0$ en $a^3 + b^3 + c^3 = 2016$, wat is dan het product $abc$?

 

Opgave 349 [niveau ooO]

In een bepaald Tibetaans klooster wonen 36 monniken. De monniken dragen vier kleuren mutsen: rood, wit, blauw en geel. Ieder van deze monniken valt onder één van de zes ordes die leven in dit klooster. Elk van de zes ordes wordt gekarakteriseerd door het dragen van twee verschillende mutsen (rood-wit), (rood-blauw), (rood-geel), (wit-blauw), (wit-geel) en (blauw-geel). Alle monniken van dezelfde orde dragen dagelijks dezelfde muts. Elke monnik weet dagelijks welke kleur is gekozen. Een toerist bezoekt het klooster vier opeenvolgende dagen en telt de mutsen van de monniken:

dag	rood	wit	blauw	geel
maandag	13	12	11	0
dinsdag	0	7	13	16
woensdag	11	12	0	13
donderdag	7	0	20	9

Uit hoeveel monniken bestaan de zes verschillende ordes?

Bekijk oplossing