Oplossing 350 [niveau oOO]

Een papier wordt opgevouwen en ziet er ná het vouwen uit als op onderstaand plaatje. De rode, blauwe, groene en gele flap zijn achtereenvolgens langs de randen $AB$, $BC$, $CD$ en $AD$ gevouwen naar punt $P$. Vouw het papier nu weer helemaal open. Toon aan dat er dan een vierhoek ontstaat.

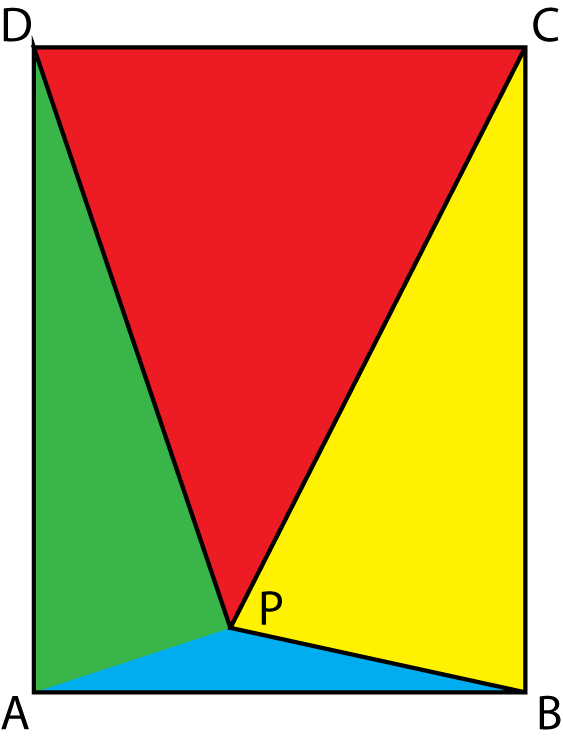
Oplossing. We klappen de vier flappen uit en tekenen de punten $K$, $L$, $M$ en $N$. Waarom is $\angle KAL=180^o$? Ga uit van de oorspronkelijke hoek $\angle DAB=90^o$. Nu geldt verder dat $\angle KAD=\angle DAP$ en $\angle LAB=\angle PAB$. Zodoende geldt: $\angle KAL=\angle KAD+\angle DAP+\angle PAB+\angle LAB=2(\angle DAP+\angle PAB)=2\cdot90^o=180^o$.

 

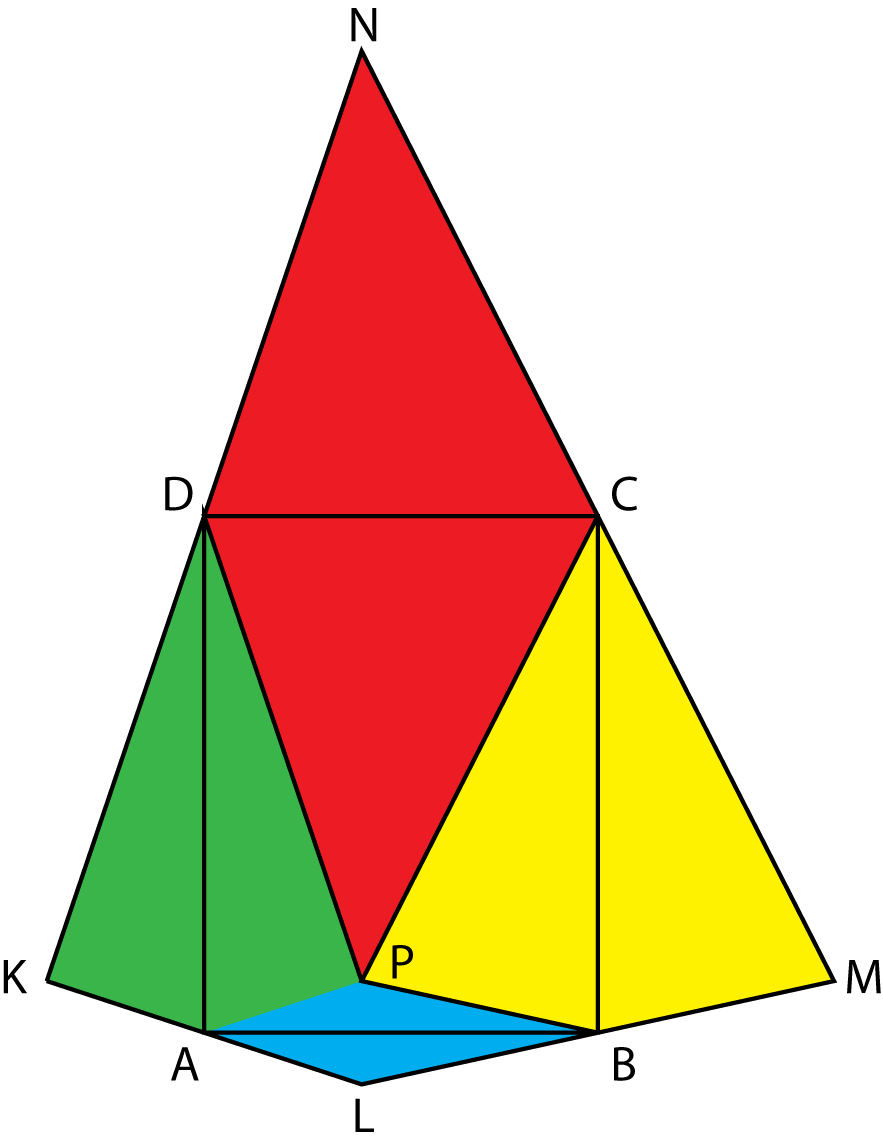
Oplossing 351 [niveau oOO]

We hebben een digitale klok, die loopt van 00:00 tot en met 23:59 (dus met een nauwkeurigheid van minuten). Soms vormen de cijfers van de klok (zonder de :) een kwadraat. In hoeveel van zulke gevallen is óók het totaal aantal minuten sinds 00:00 een kwadraat? Een voorbeeld van zo’n tijdstip is 01:21, want 121 is een kwadraat (namelijk 11²), en 01:21 is 81 minuten na 00:00, wat ook een kwadraat is (namelijk 9²).
Oplossing. De kwadraten tot 2359 moeten gecontroleerd worden. Dat zijn er niet zo veel, en daarom loont het nauwelijks de moeite om de oplossingen door middel van vergelijkingen te vinden. We vinden direct 0² = 0, 1² = 1, 2² = 4, 3² = 9, 4² = 16, 5² = 25, 6² = 36 en 7² = 49. Daarna zijn de oplossingen schaars. Er zijn nog twee andere oplossingen: 9² = 81 met 1:21 = 11² en 35² = 1225 met 20:25 = 45².

 

Oplossing 352 [niveau ooO]

Hieronder zie je een serie steeds kleiner wordende vierkanten. Het grootste vierkant is 90 × 90 cm². Als je naar rechts gaat is elk volgend vierkant half zo hoog als het voorafgaande. De linker onderhoek ligt steeds op tweederde deel van de onderzijde. Bepaal de totale oppervlakte van het gebied dat door de vierkanten wordt bedekt.

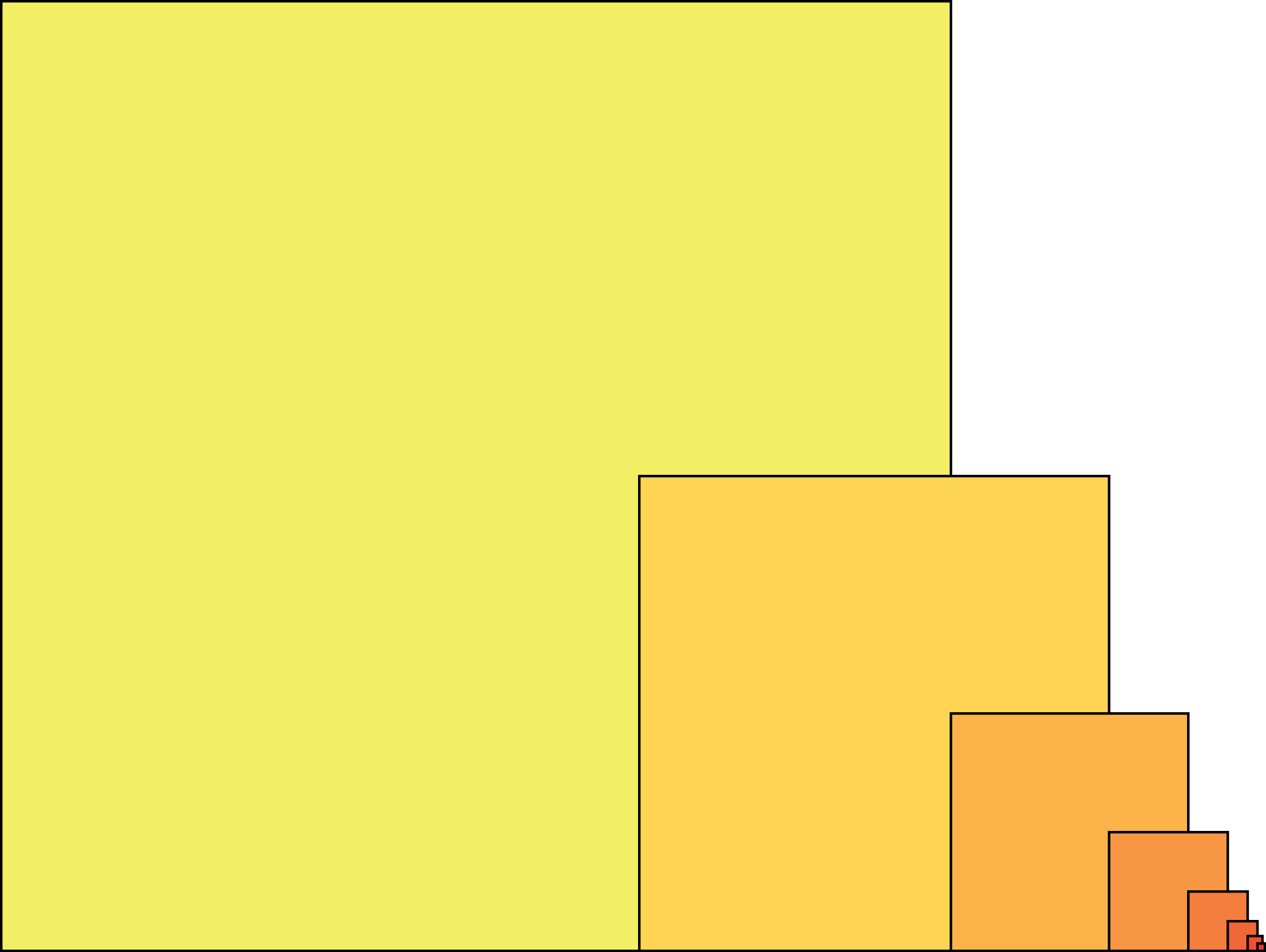
Oplossing. We kleuren de figuur op een iets andere manier in, zodat de oppervlaktes van de verschillend gekleurde gebieden eenvoudig te berekenen zijn:

De rechthoek pal naast het vierkant heeft afmetingen ${1 \over 6} \times {1 \over 2}$. Elke volgende rechthoek is half zo breed en half zo hoog. Met de formule voor de som van een meetkundige rij vinden we voor de totale oppervlakte:
\(\begin{eqnarray*} &&90^2\cdot(1+{1 \over 6} \cdot {1 \over 2} + {1 \over 12} \cdot {1 \over 4} + ...) =\\ && 90^2\cdot(1+{1 \over 12} (1 + {1 \over 4} + {1 \over 4^2} + {1 \over 4^3} + ...))=\\ && 90^2\cdot(1+{1 \over 12} \cdot {4 \over 3}) = 90^2 \cdot {10 \over 9} = 9000. \end{eqnarray*}\)

 

Oplossing 353 [niveau ooO]

De getallen $a$, $b$ en $c$ voldoen aan de volgende twee vergelijkingen:
\(\begin{eqnarray*} a + b + c + abc &=& 0\\ ab + ac + bc + 1 &=& 0 \end{eqnarray*}\)
Vind alle oplossingen $(a, b, c)$.
Oplossing. Tel de twee vergelijkingen bij elkaar op:
$$abc + ab + ac + bc + a + b + c + 1 = 0.$$
Het linkerlid kun je ontbinden in drie factoren:
$$abc + ab + ac + bc + a + b + c + 1 = (a + 1)(b + 1)(c + 1).$$
Als $(a + 1)(b + 1)(c + 1) = 0$, is minimaal één van de variabelen $a$, $b$, $c$ gelijk aan $–1$.
Trek nu de twee gegeven vergelijkingen van elkaar af:
$$abc – ab – ac – bc + a + b + c – 1 = 0.$$
Ook nu kun je het linkerlid ontbinden in drie factoren:
$$abc – ab – ac – bc + a + b + c – 1 = (a – 1)(b – 1)(c – 1).$$
Als $(a – 1)(b – 1)(c – 1) = 0$, is minimaal één van de variabelen $a$, $b$, $c$ gelijk aan $1$.
Stel $a = 1$ en $b = –1$ en kies $c$ willekeurig, dan voldoen deze getallen aan beide vergelijkingen. Dit geldt voor een willekeurige keuze van twee van de drie variabelen. Er zijn dus zes series van oplossingen:
\(\begin{eqnarray*} &&\{n, 1, –1\}, \{n, –1, 1\}, \{1, n, –1\},\\ &&\{–1, n, 1\}, \{1, –1, n\}, \{–1, 1, n\}. \end{eqnarray*}\)