Opgave 350 [niveau oOO]

Een papier wordt opgevouwen en ziet er ná het vouwen uit als op onderstaand plaatje. De rode, blauwe, groene en gele flap zijn achtereenvolgens langs de randen $AB$, $BC$, $CD$ en $AD$ gevouwen naar punt $P$. Vouw het papier nu weer helemaal open. Toon aan dat er dan een vierhoek ontstaat.

 

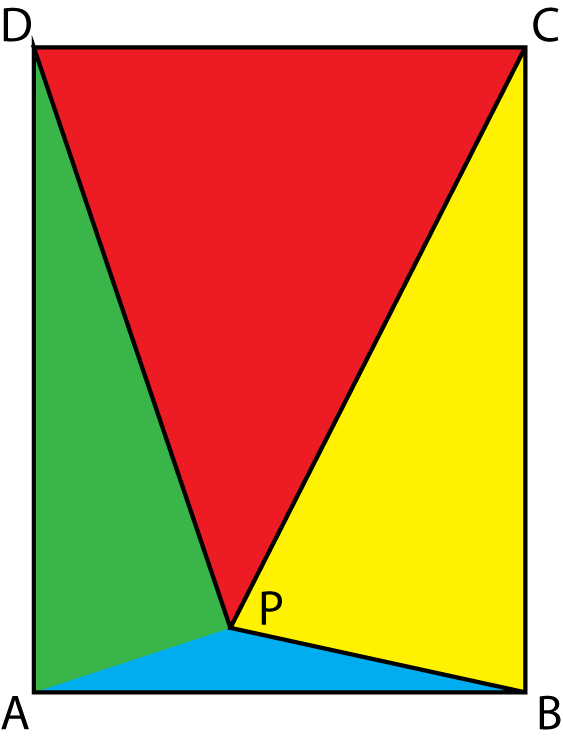
Opgave 351 [niveau oOO]

We hebben een digitale klok, die loopt van 00:00 tot en met 23:59 (dus met een nauwkeurigheid van minuten). Soms vormen de cijfers van de klok (zonder de :) een kwadraat. In hoeveel van zulke gevallen is óók het totaal aantal minuten sinds 00:00 een kwadraat? Een voorbeeld van zo’n tijdstip is 01:21, want 121 is een kwadraat (namelijk 11²), en 01:21 is 81 minuten na 00:00, wat ook een kwadraat is (namelijk 9²).

 

Opgave 352 [niveau ooO]

Hieronder zie je een serie steeds kleiner wordende vierkanten. Het grootste vierkant is 90 × 90 cm². Als je naar rechts gaat is elk volgend vierkant half zo hoog als het voorafgaande. De linker onderhoek ligt steeds op tweederde deel van de onderzijde. Bepaal de totale oppervlakte van het gebied dat door de vierkanten wordt bedekt.

 

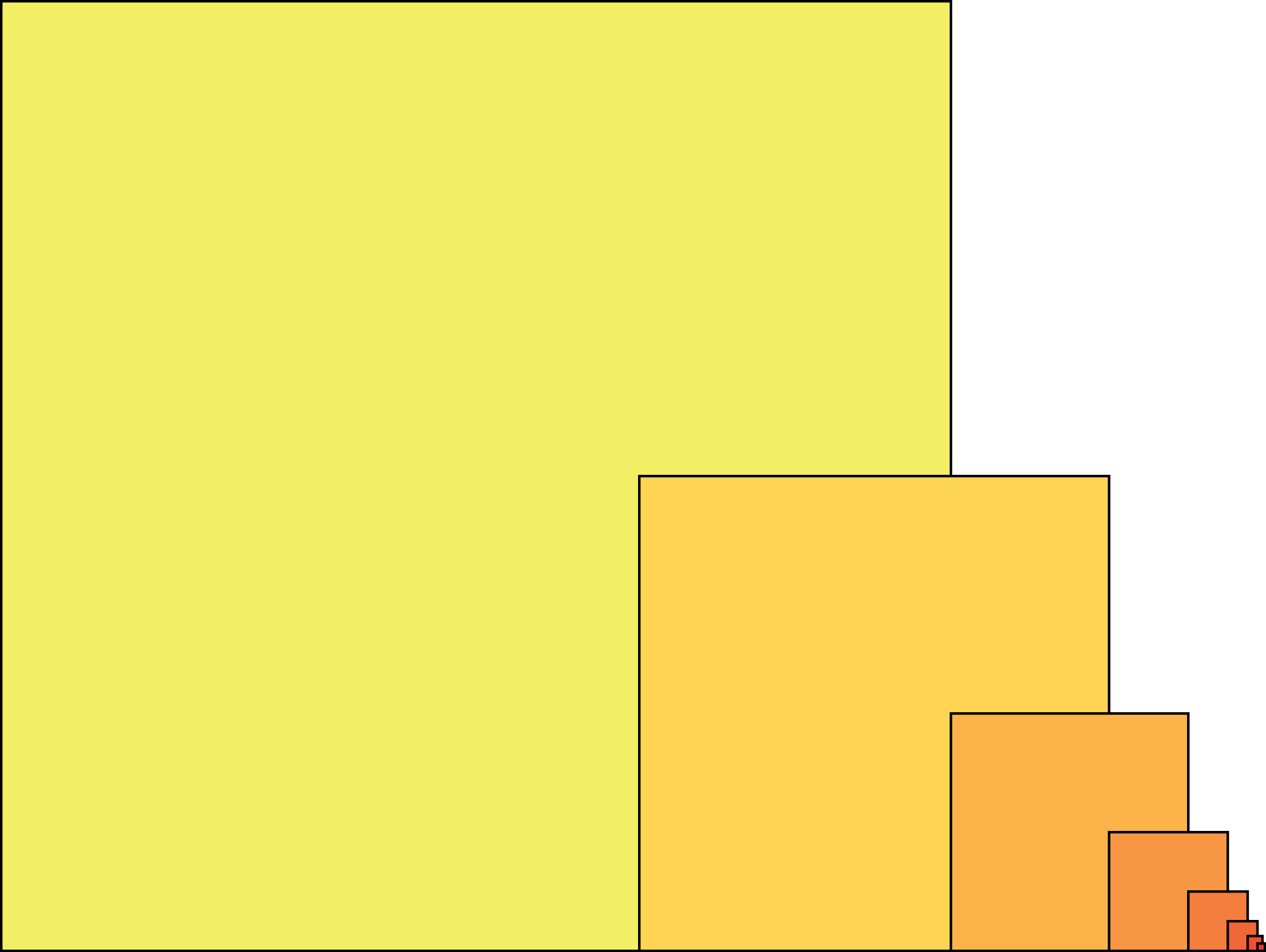
Opgave 353 [niveau ooO]

De getallen $a$, $b$ en $c$ voldoen aan de volgende twee vergelijkingen:
\(\begin{eqnarray*} a + b + c + abc &=& 0\\ ab + ac + bc + 1 &=& 0 \end{eqnarray*}\)
Vind alle oplossingen $(a, b, c)$.

 

 

Bekijk oplossing