Opgave 417 [Niveau oOO]

We definiëren het punt $C'$ als het punt dat een afstand van $15$ boven en $20$ rechts van het punt $B$ ligt. We kunnen dan berekenen dat $|C'D|= \sqrt{15^2 + 20^2} = 25$ We concluderen dat zowel $C$ als $C'$ snijpunten zijn van de cirkel met middelpunt $D$ en straal $25$, en de cirkel met middelpunt $A$ en straal $39$. Een van deze snijpunten ligt echter aan de andere kant van $AD$ dan $C$ en $C'$. Daarom moet wel gelden dat $C = C'$. We berekenen nu eenvoudig dat $|BC|= |BC'| = \sqrt{15^2 + 20^2} = 25$.

 

Opgave 418 [niveau oOO]

Naïef kunnen we elk van de drie vakjes kleuren met één van de vier beschikbare kleuren. Dit geeft $64$ mogelijkheden. Echter, sommige stenen worden hetzelfde na draaiing, dus we moeten tellen hoe vaak dit gebeurt. Er zijn precies $4$ verschillende Triominos-stenen te maken die uit slechts een enkele kleur bestaan. Als een Triominos- steen bestaat uit meer dan één kleur, dan kan deze altijd door draaiing worden overgevoerd in drie verschillende configuraties. Omdat er $60$ mogelijke kleurringen waren met meer dan één kleur, volgt dat men zo maar $\frac{60}{3} = 20$ verschillende Triominos- stenen kan maken. In totaal hebben we dus $4 + 20 = 24$ Triominos-stenen.

Opgave 419 [niveau ooO]

We nemen een willekeurige stapel van $20$ van de munten apart van de rest. Al deze munten draaien we om. We beweren dat nu in beide stapels evenveel munten de zilveren kant boven hebben. Namelijk, veronderstel dat er onder de $80$ overgebleven munten nog precies $Z$ munten met de zilveren kant boven lagen. Dan lagen er dus voor het omdraaien van de andere stapel daar nog $20 - Z$ munten met de zilveren kant boven, en zo lagen er nog $20 - (20 - Z) = Z$ munten met de gouden kant boven. Wanneer we nu alle munten in deze stapel omdraaien, liggen er hier dus precies $Z $ munten met de zilveren kant boven, precies zoals verlangd.

Opgave 420 [niveau ooO]

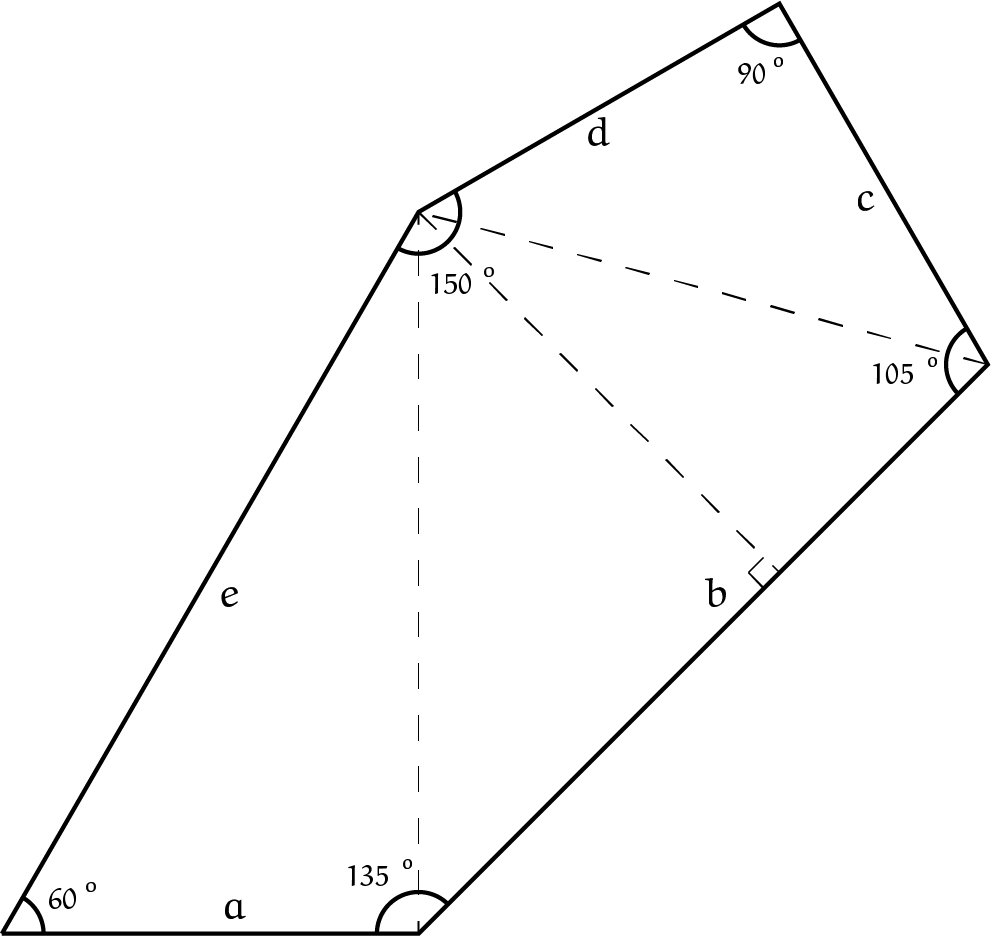
Linksonder in de figuur bevindt zich een 30-60-90-driehoek met zijden $1, \sqrt 3$ en $2$. De oppervlakte van deze driehoek is $\frac12\sqrt 3$. Rechtsboven in de figuur bevindt zich een 45-45-90-driehoek met zijden $1, 1$ en $\sqrt 2$ De oppervlakte van deze driehoek is $\frac12$. Nu resteert de oppervlakte van de centrale driehoek. Laten we een hoogtelijn op de zijde met lengte $b$ neer, dan zien we dat deze driehoek wordt opgedeeld in twee driehoeken. De driehoek linksonder is dan een 45-45-90-driehoek met zijden $\sqrt 3/\sqrt 2, \sqrt 3\sqrt 2 $ en $\sqrt 3$. Deze driehoek heeft oppervlakte $ \frac34$. De driehoek rechtsboven is nu een 30-60-90-driehoek met zijden $\frac12\sqrt 2$, $\sqrt 3/\sqrt 2$ en $\sqrt 2$. De driehoek heeft oppervlakte $\frac14\sqrt 3$. Alles tezamen vinden we dat de oppervlakte van de figuur gelijk is aan $\frac12\sqrt 3 + \frac12 + \frac34 + \frac14\sqrt 3 = (5 + 3\sqrt 3)4$.

Voor het bonuspunt:

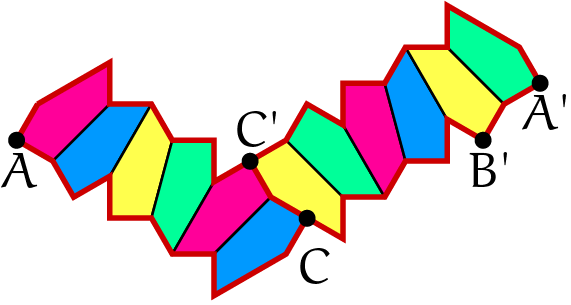
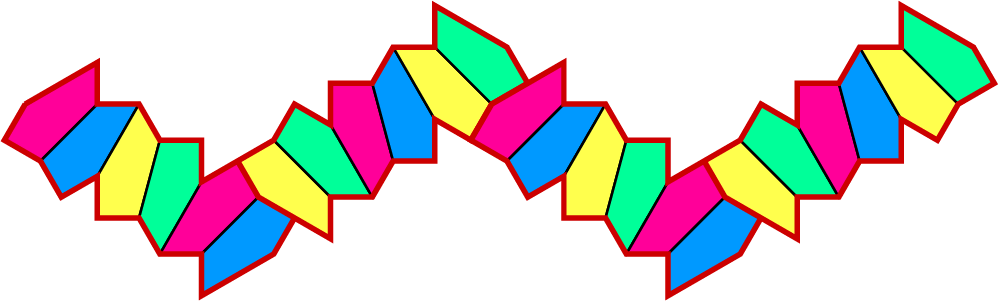
Om te beginnen kan worden opgemerkt dat twee patronen van $12$ figuren exact horizontaal en verticaal naast elkaar liggen. Verticaal is gemakkelijk in te zien. Om dat horizontaal in te zien splitsen we de $12$ figuren op in tweemaal $6$ figuren (zie figuur). De twee halve patronen zijn gespiegeld t.o.v. elkaar. Daarom is het hoogteverschil van $A$ en $C$ hetzelfde als het hoogteverschil van $A'$ en $C'$. Ook zijn de hoogteverschillen tussen $A'$ en $B'$ en tussen $C$ en $C'$ gelijk. In de onderste figuur is te zien dat bij $B'$ een nieuw patroon begint. Dat is dus op dezelfde hoogte als $A$. We merken op dat de verticale verschuiving gelijk is
aan $1 + \sqrt3$.
Voor de horizontale verschuiving doen we iets slims.
De oppervlakte van $12$ figuren is

$$12\cdot(5 + 3\sqrt3)/4 = 15 + 9\sqrt3.$$

De horizontale verschuiving is precies gelijk aan het quotiënt van de oppervlakte van het patroon en de verticale verschuiving, dus

$$\frac{15+9\sqrt3}{1+\sqrt3}=\frac12\cdot(\sqrt3-1)\cdot(15+9\sqrt3)=6+3\sqrt3.$$