Inzenden kan alleen per e-mail. Stuur je oplossing (getypt of een scan of foto van een handgeschreven oplossing) naar [email protected]. Je ontvangt een automatisch antwoord zodra we je bericht hebben ontvangen.
Voorzie het antwoord van een duidelijke toelichting (dat wil zeggen: een berekening of een bewijs). Vermeld je naam en adres; leerlingen moeten ook hun klas en de naam van hun school vermelden.
Je inzending moet bij ons binnen zijn vóór 1 februari 2020.

Opgave 417 [oOO]

Zij $ABCD$ een convexe vierhoek met hoek $ABD = 90^{\rm o}.$ Veronderstel dat $|AB| = 16, |BD| = 30, |CD| = 25$ en $|AC| = 39.$ Bepaal $|BC|.$

Opgave 418 [oOO]

Triominos vereist dat je cijfers moet kunnen lezen. Een fabrikant ontwerpt een vereenvoudigde versie van Triominos met vier kleuren geel, blauw, groen en rood. Hoeveel verschillende Triominos-stenen bestaan er? Elke Triominos-steen kan worden voorzien van één, twee of drie kleuren. De onderstaande twee stenen bevatten weliswaar dezelfde kleuren, maar zijn toch verschillend.

Opgave 419 [ooO]

Je zit in een donkere ruimte met een stapel van $100$ munten. Ze hebben allemaal een zilveren en een gouden kant. Twintig liggen met de zilveren kant boven, tachtig met de gouden kant, maar je weet niet welke. Je moet twee stapels maken met hetzelfde aantal zilveren munten boven. Je kan niets zien en beide kanten van de munten voelen hetzelfde. Je mag wel zoveel munten verplaatsen of omdraaien als je wilt, en de twee uiteindelijke stapels hoeven niet even groot te zijn.

Opgave 420 [ooO]

In het artikel over vlakvullingen in dit nummer van Pythagoras staan 15 vlakvullingen met vijfhoeken. Eén van die vijfhoeken staat hieronder getekend.

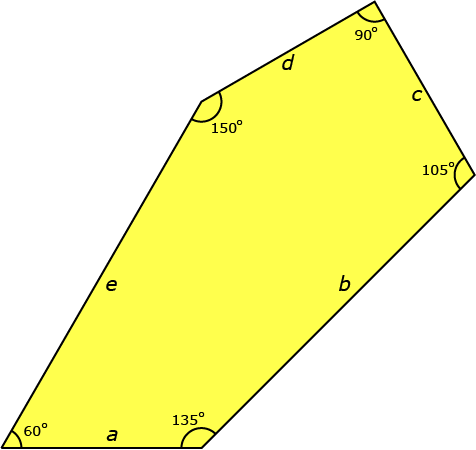1. Bepaal de oppervlakte van de vijfhoek (uitgaande dat $a = c = d = 1, e = 2$ en $b = \frac12(\sqrt2 + \sqrt6).$
2. (Bonuspunt) De vlakvulling ontstaat door een minimaal patroon herhaaldelijk naast elkaar neer te leggen. Dit minimale patroon (stempel) kan op verschillende manieren worden gekozen. Er is gekozen voor het volgende minimale patroon:
   

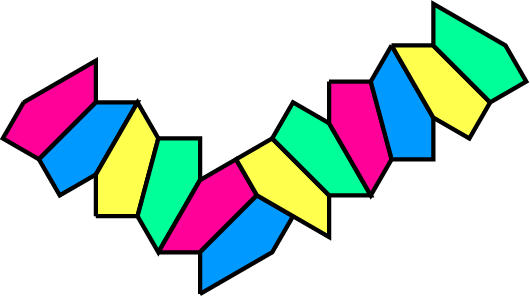
Bepaal over welke afstand dit figuur in (min of meer) horizontale en verticale richting moet worden verplaatst, zodat het gehele vlak bedekt zal worden.

Bekijk oplossing