Opgave 421 [oOO]

De diagonaal van het vierkant $PQRS$ heeft dezelfde lengte als de diameter van de cirkel. Omdat de cirkel precies in het vierkant past, is zijn diameter gelijk aan de hoogte van het vierkant; dus $|PR| = 10$. Dit betekent dat de zijde van vierkant $PQRS$ gelijk is aan $\frac{10}{\sqrt{2}} = 5\sqrt{2}$. De oppervlakte is dan gelijk aan $(5\sqrt{2})^2 = 50$.

Opgave 422 [oOO]

Rijtjes getallen met de eigenschap uit de opgave kunnen niet twee dezelfde getallen hebben. Daarom moeten $a, b, c$ en $d$ allemaal verschillend zijn en dus is $a - d \ge 3$. Als $a - d = 3$, dan is het viertal gelijk aan $a, a + 1, a + 2, a + 3$. Echter, dan geldt $a + (a + 3) = (a + 1) + (a + 2)$, en dus heeft dit rijtje ook niet de eigenschap uit de opgave.
Er geldt dus $a - d \ge 4$. We beweren dat $4$ de kleinst mogelijke waarde van $a - d$ is. Namelijk, deze rijtjes zien eruit als $a, a + 1, a + 2, a + 4$, of als $a, a + 1, a + 3, a + 4$, of als $a, a + 2, a + 3, a + 4$. In het tweede geval geldt altijd $a + (a + 4) = (a + 1) + (a + 3)$ en dus is dat nooit mogelijk. De andere twee mogelijkheden geven voor sommige waarden van $a$ wel rijtjes die aan de gevraagde eigenschappen voldoen. Voor het eerste geval is het rijtje $4, 5, 6, 8$ het kleinst mogelijke mooie rijtje, en in het laatste geval het rijtje $3, 5, 6, 7$. Van deze twee heeft $3, 5, 6, 7$ de laagste som van de cijfers.

Opgave 423 [ooO]

Het antwoord is ja, en het kan zelfs door enkel $a = 2$ en $b = 3$ te gebruiken. Namelijk, elk gehele getal $n \ge 2$ kan geschreven worden in de vorm $n = 2x + 3y$ met $x, y$ niet-negatieve gehele getallen. Namelijk, voor $n$ even kiezen we $x = n/2$ en $y = 0$, en voor $n$ oneven kiezen we $x = (n – 3)/2$ en $y = 1$. Dit betekent voor elk priemgetal dat $p^n = p^{2x} \cdot p^{3y}$. Als we nu een willekeurig getal bekijken en het schrijven als product van priemmachten $p^{n_i}_i$ dan krijgen we dat 

$$p^{n_1}_1 \cdots p^{n_k}_k = p^{2x_1}_1p^{3y_1}_1\cdots p^{2x_k}_kp^{3y_k}_k = (p^{x_1}_1 \cdots p^{x_k}_k)^2 \cdot (p^{y_1}_1 \cdots p^{y_k}_k)^3,$$

en dat is van de gevraagde vorm.

Opgave 424 [ooO]

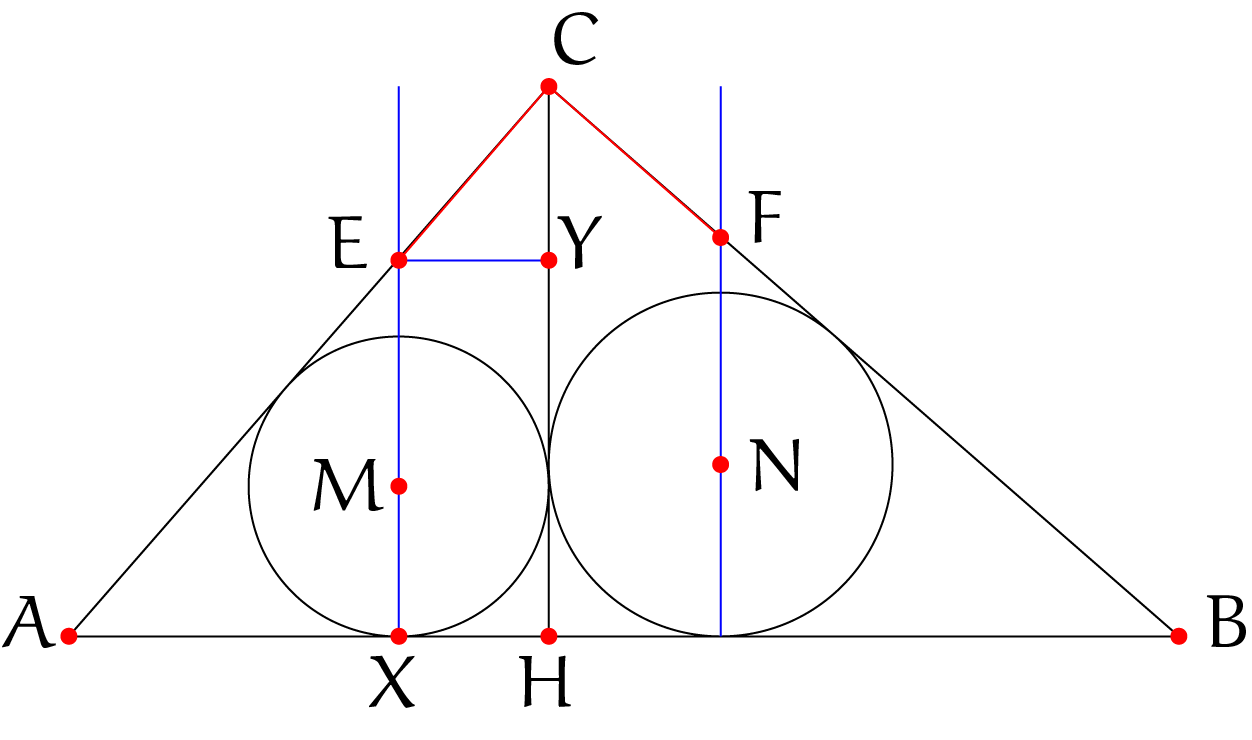
Laat $X$ het snijpunt zijn van het verlengde van $EM$ met $AB$ en laat $Y$ het punt op $CH$ zijn zodat $EY$ loodrecht staat op $CH$. Merk nu op dat $|MX| = |XH|$ omdat $MH$ de bissectrice is van een rechte hoek, waardoor $\angle XHM = 45^{\rm o}$. We zien dat $|XH|$, en daarmee ook $|EY|$, gelijk is aan de straal van de ingeschreven cirkel van $\Delta AHC$. Welnu, omdat $\Delta CEY$ en $\Delta CAH$ gelijkvormig zijn, volgt dat $|CE| / |EY| = |CA| / |AH|$. Aan de andere kant zijn ook $\Delta CAH$ en $\Delta BAC$ gelijkvormig en de vergrotingsfactor is precies gelijk aan $|CA| / |AH|$. Dit betekent dat de stralen van de ingeschreven cirkels schalen met dezelfde factor. Als we dit nu combineren met de eerder gevonden verhouding en het feit dat $|EY|$ gelijk was aan de straal van de ingeschreven cirkel van $\Delta AHC$, dan volgt dat $|CE|$ gelijk is aan de straal van de ingeschreven cirkel van driehoek $\Delta ABC$. Met een geheel analoog argument kunnen we bewijzen dat $|CF|$ ook gelijk is aan de straal van de ingeschreven cirkel van $\Delta ABC$. In het bijzonder geldt dus $|CE| = |CF|$.