Pythagoras Olympiade 59-4, februari 2020
Inzenden kan alleen per e-mail. Stuur je oplossing (getypt of een scan of foto van een handgeschreven oplossing) naar [email protected]. Je ontvangt een automatisch antwoord zodra we je bericht hebben ontvangen.
Voorzie het antwoord van een duidelijke toelichting (dat wil zeggen: een berekening of een bewijs). Vermeld je naam en adres; leerlingen moeten ook hun klas en de naam van hun school vermelden.
Je inzending moet bij ons binnen zijn vóór 16 april 2020.
Opgave 421 [oOO]
Laat $ABCD$ een vierkant zijn met zijde $10$ en laat $PQRS$ het vierkant zijn dat wordt gevormd door de snijpunten van de diagonalen van het vierkant met zijn ingeschreven cirkel. Bepaal de oppervlakte van vierkant $PQRS$.
Opgave 422 [oOO]
Er bestaan rijtjes van vier positieve gehele getallen $a\ge b\ge c\ge d$ met de eigenschap dat als je een of meer getallen van de vier uitkiest en optelt, je voor verschillende keuzes altijd een verschillend antwoord krijgt. Zulke rijtjes met de extra eigenschap dat de waarde van $a-d$ zo klein mogelijk is, noemen we mooi. Vind het mooie rijtje waarvan de som van de getallen minimaal is.
Opgave 423 [ooO]
Een getal heet kwadraatvol als geldt dat voor elke priem die dit getal deelt, ook het kwadraat van de priem dit getal deelt. Zo zijn bijvoorbeeld $36$, $72$, $108$ en $72000$ kwadraatvol. Echter, $54$ is niet kwadraatvol, want $2$ deelt $54$ maar $4$ deelt $54$ niet.
Is elk kwadraatvol getal te schrijven als $m^an^b$, met $m$, $n$, $a$, $b$ positieve gehele getallen waar bovendien $a$ en $b$ groter zijn dan $1$? Zo niet, bepaal het kleinste kwadraatvolle getal dat niet zo te schrijven is.
Opgave 424 [ooO]
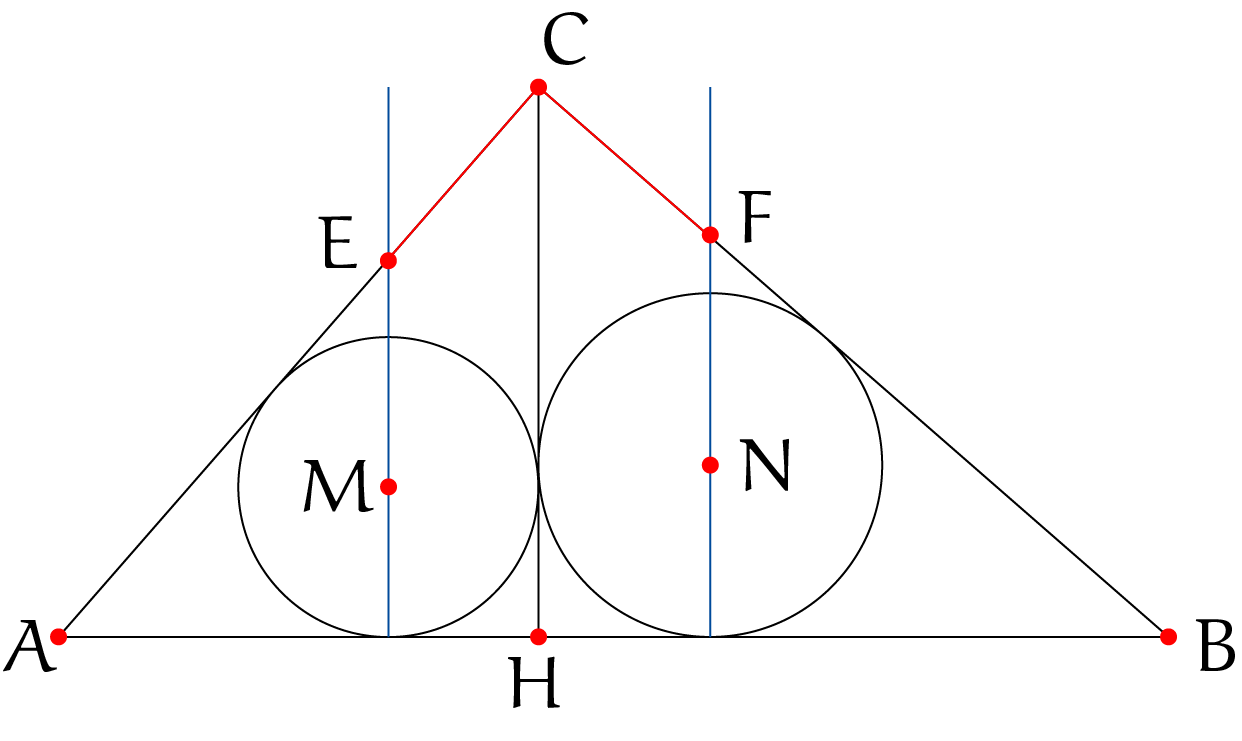
Gegeven is de rechthoekige driehoek $\Delta ABC$ en laat $H$ op lijnstuk $AB$ liggen zodat $CH$ loodrecht staat op $AB$. Zij $M$ het middelpunt van de ingeschreven cirkel van $\Delta ACH$ en $N$ dat van $\Delta BCH$. Laat $E$ en $F$ liggen op respectievelijk de lijnstukken $AC$ en $BC$ zodat $EM$ en $FN$ beide evenwijdig zijn aan $CH$. Toon aan dat de lijnstukken $CE$ en $CF$ even lang zijn.