Opgave 441

Voor $n = 1$ en $n = 2$ werkt iedere kleuring, omdat er geen twee verschillende getallen zijn met een even som. Voor $n = 4$ is het ook mogelijk: kleur $1$ en $2$ rood en $3$ en $4$ blauw. Voor $n = 3$ ook, laat dan knikker 4 weg.

Voor $n \geq 5$ is het niet mogelijk. We bewijzen dit uit het ongerijmde. Stel dat we een kleuring hebben voor een zekere $n \geq 5$. Omdat $1 + 3 = 4$ even is, hebben $1$ en $3$ verschillende kleuren. Omdat $1 + 5$ even is, hebben $1$ en $5$ verschillende kleuren. Omdat er maar twee kleuren zijn, betekent dit dat $3$ en $5$ dezelfde kleur hebben. Maar dat mag niet, omdat $3 + 5$ even is; een tegenspraak. Dus voor $n \geq 5$ is zo'n kleuring niet mogelijk.

Het is dus precies mogelijk voor alle $n \leq 4$.

Opgave 442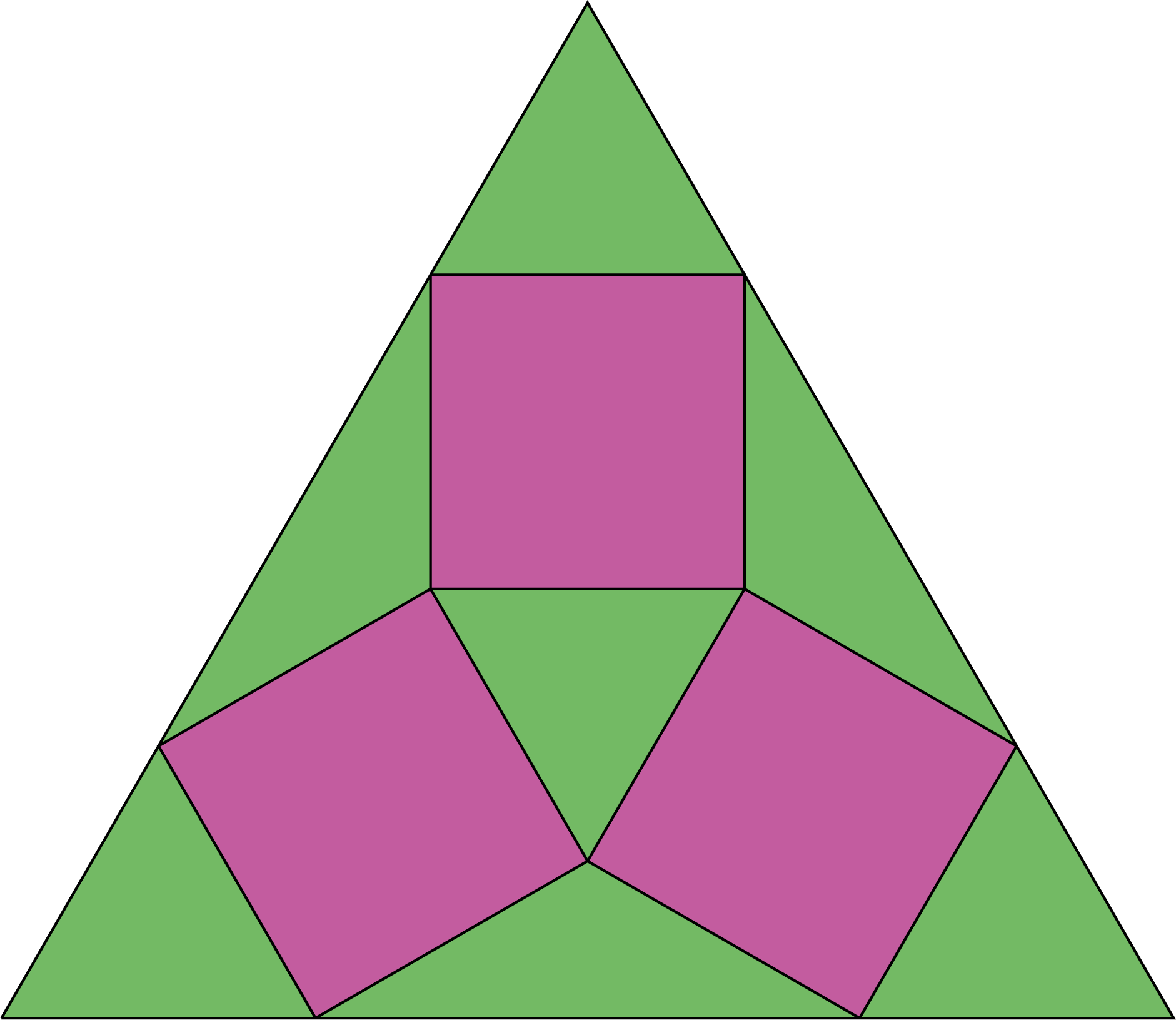

Het groene gedeelte bestaat uit $4$ gelijkzijdige driehoeken, voor het gemak stellen we de zijde van deze driehoek op $1$.

Er zijn ook $3$ groene driehoeken met hoeken van $30$, $30$ en $120$ graden. We beweren dat zo'n driehoek dezelfde oppervlakte heeft als een gelijkzijdige driehoek met zijde $1$. Namelijk, als we zo'n driehoek in tweeën knippen via een loodlijn vanuit de hoek van $120^{\rm o}$ en de twee stukjes met de hoeken van $30^{\rm o}$ bij elkaar leggen, krijgen we een driehoek met tophoek $60^{\rm o}$ en twee aanliggende zijden met lengte $1$. Met andere woorden, een gelijkbenige driehoek met een tophoek van $60^{\rm o}$; een gelijkzijdige driehoek met zijde $1$.

De oppervlakte van het groene gedeelte is dus even groot als $7$ gelijkzijdige driehoeken met zijdelengte $1$. Een hoogtelijn van zo'n driehoek is met de stelling van Pythagoras gelijk aan $\tfrac{1}{2}\sqrt{3}$. De oppervlakte van een zo'n driehoek is dus gelijk aan $\tfrac{1}{4}\sqrt{3}$, dus het groene gedeelte heeft oppervlakte $\tfrac{7}{4}\sqrt{3}$.

Het paarse gedeelte bestaat dan uit $3$ vierkanten op zijdelengte $1$, en heeft dus oppervlakte $3$. De verhouding is dus: 
$$\frac{\mbox{paars}}{\mbox{groen}} = \frac{3}{\tfrac{7}{4}\sqrt{3}} = \frac{4\sqrt{3}}{7} \approx 0{,}990$$

Opgave 443

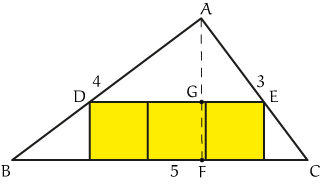
Noem de lengte van de gezochte zijde $x$. Noem het punt waarin het linker vierkant de zijde $AB$ raakt $D$, en het punt waar het meest rechtse vierkant zijde $AC$ raakt $E$. Teken een hoogtelijn vanuit $A$ op $BC$: noem het snijpunt met $BC$ even $F$, en met $DE$ ten slotte $G$.

Door op twee verschillende manieren de oppervlakte van $\triangle ABC$ uit te rekenen, vinden we dat $$\frac{1}{2}|AB||AC| = \frac{1}{2}|BC||AF|$$ Invullen $|AB| = 4$, $|AC| = 3$, $|BC| = 5$ geeft ons dat $|AF| = \frac{12}{5}$.

De twee driehoeken $\triangle ABC$ en $\triangle ADE$ zijn gelijkvormig, en daarmee vinden we $$\frac{|BC|}{|DE|} = \frac{|AB|}{|AD|}.$$ Omdat driehoeken $\triangle ABF$ en $\triangle ADG$ gelijkvormig zijn, vinden we dat $$\frac{|AB|}{|AD|} = \frac{|AF|}{|AG|}.$$ Hieruit volgt de gelijkheid $$\frac{|BC|}{|DE|} = \frac{|AF|}{|AG|}.$$ Nu weten we dat $|BC| = 5$ en $|AF| = \frac{12}{5}$. Omdat de zijdelengte van een vierkantje $x$ is, vinden we dat $|DE| = 3x$ en $|AG| = \frac{12}{5} - x$. Hiermeee kunnen we de vergelijking oplossen. 

\[
    \frac{5}{3x}  = \frac{\frac{12}{5}}{\frac{12}{5} - x} \implies \frac{5}{3x} = \frac{12}{12 - 5x}
\]
en na kruislinks vermenigvuldigen
\[
    5(12 - 5x)  = 12 \cdot 3x \implies 60 - 25x = 36x.
\]
We zien dat $61x = 60$, en dus $x = 60/61$.

Opgave 444

Deze opgave is erg lastig, tot je hem ziet. Als we de twee vergelijkingen bij elkaar optellen, vinden we $$a^2 - c^2 = (a + b)c$$ Als we beide kanten met $a - b$ vermenigvuldigen, vinden we dat 

$(a^2 - c^2)(a - b) = (a^2 - b^2)c$

$a^3 - a^2b - ac^2 + bc^2 = bc^2$

$a^3 - a^2b - ac^2 = 0$.

Aangezien $a \neq 0$ kunnen we delen door $a$, waarna we vinden dat $$a^2 - c^2 - ab = 0.$$ Dus $a^2 - c^2 = ab$, zoals gevraagd.