Opgave 441 ^[oOO]

Zij $n \ge 1$ een natuurlijk getal. We proberen elk van de getallen $1$ tot en met $n$ rood of blauw te kleuren zodat ieder tweetal $a$, $b$ van verschillende getallen met $a + b$ even eraan voldoet dat $a$ en $b$ verschillende kleuren hebben. Voor welke $n$ is dit mogelijk?

Opgave 442 ^[oOO]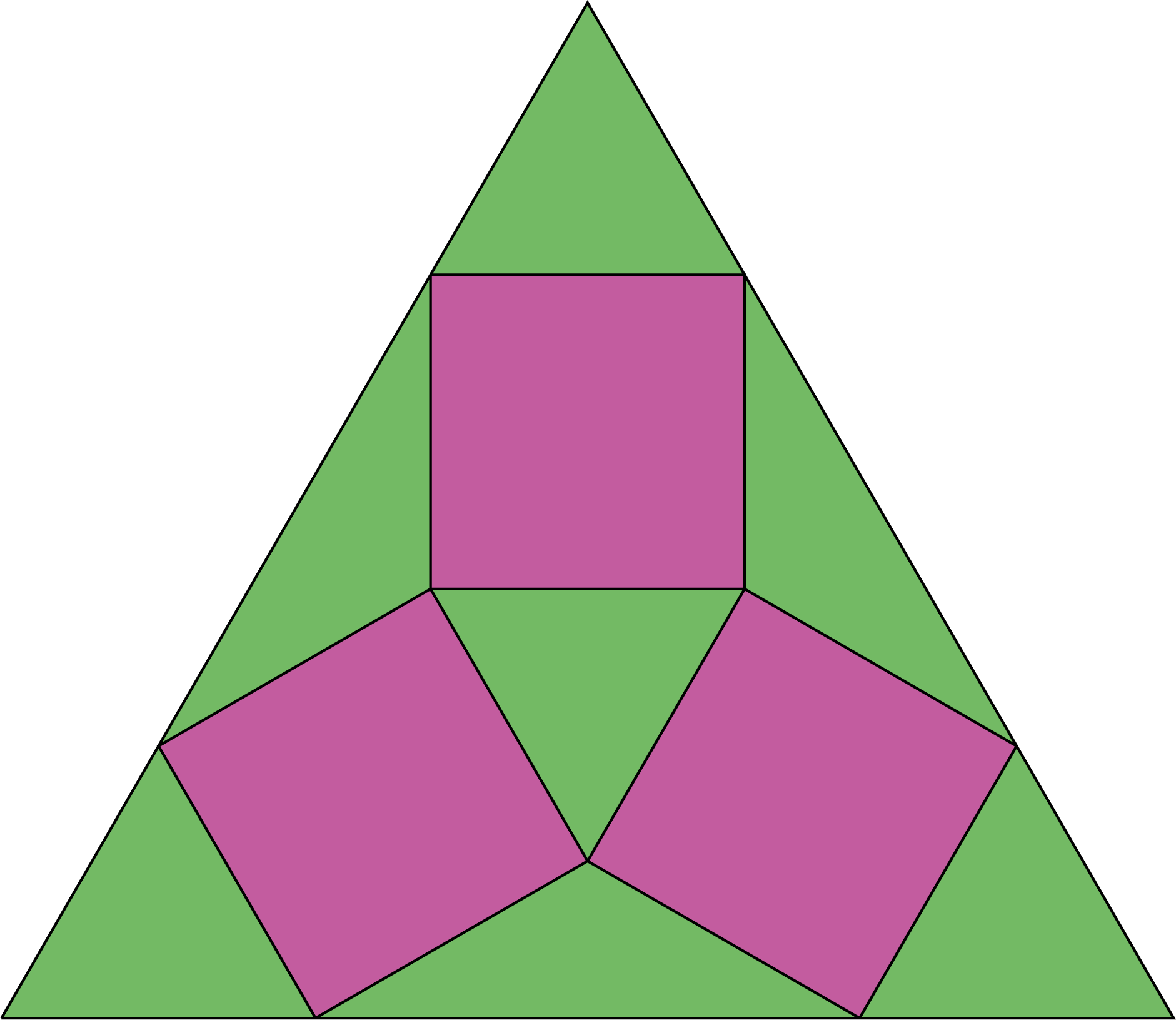

In een gelijkzijdige driehoek worden drie even grote vierkanten geplaatst zoals in de figuur rechts.

Wat is de verhouding tussen de oppervlaktes van het paarse en het groene deel?

Opgave 443 ^[ooO]

In een rechthoekige driehoek $ABC$ geldt $|AB| = 4$, $|AC| = 3$ en $|BC| = 5$. Op zijde $BC$ worden drie even grote vierkantjes geplaatst zoals in de figuur links.

Bepaal de lengte van de zijdes van deze vierkantjes.

 

 

 

Opgave 444 ^[ooO]

Laat $a$, $b$ en $c$ reële getallen ongelijk aan $0$ zijn waarvoor geldt dat $a^2 - b^2 = bc$ en $b^2 - c^2 = ca$. Bewijs dat $a^2 - c^2 = ab$.

Bekijk oplossing