opgave 445 ^[oOO]

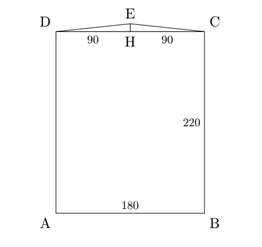
De omtrek van het schilderij is $220 + 220 + 180 + 180 = 800\ cm$. Dus het touw heeft lengte $801$ cm. Het stuk touw $|DE| + |EC|$ heeft dus lengte $801 - 220 - 220 - 180 = 181\ cm$. $|EC|$ heeft dus lengte $181/2 = 90{,}5\ cm$. Immers: $|HC| = |DC|/2 = 180/2 = 90\ cm$. Met de stelling van Pythagoras kunnen we berekenen dat $|EC|^2 = |EH|^2 + |HC|^2$. Dus $|EH| = \sqrt{90{,}5^2 - 90^2} = 9{,}5\ cm$. Het schilderij hangt dus $9{,}5\ cm$ onder het hangpunt van het touw.

In de tweede gekantelde situatie geldt $|CD| = 220$. Dus dan geldt dat $|EH| = \sqrt{110{,}5^2 - 110^2} = 10{,}5\ cm$.

Opgave 446 ^[oOO]

Definieer de functie $S : N^2 \rightarrow Z$ zodanig dat $S(n, k)$ gelijk is aan het aantal mogelijke bronvermeldingen met lengte $n$ en hoogste getal $k$. Merk op dat $S(n, k) = S(n - 1, k - 1) + k \cdot S(n - 1, k)$. Immers, alle bronvermeldingen met lengte $n$ en hoogste getal $k$ kunnen we vinden door ofwel bron $k$ toe te voegen aann bronvermelding met lengte $n - 1$ hoogste getal $k - 1$, ofwel een willekeurige bron van $1$ tot en met $k$ toe te voegen aan een bronvermelding met hoogste getal $k$ en lengte $n - 1$. (We tellen hier niet dubbel, omdat de eerste $n - 1$ bronnen steeds verschillend zijn wanneer bron $n$ gelijk is bij twee bronvermeldingen.)

Het is niet lastig om in te zien dat $S(n, 1) = 1$ voor alle natuurlijke $n$ (er is maar één bronvermelding die uit slechts bron $1$ bestaat voor elke lengte), en $S(n, k) = 0$ voor alle natuurlijke $n$, $k$ als $n < k$. 

We vullen aan de hand van deze regels de volgende tabel voor $S(n, k)$ in: zie tabel 1.

We waren geïnteresseerd in $\sum_{i=1}^n S(n, i)$ (het aantal bronvermeldingen met lengte $5$), en deze waarde hebben we gevonden: $52$.

		$k$
		$1$	$2$	$3$	$4$	$5$	$\sum_{i=1}^n S(n, i)$
$n$	$1$	$1$	$0$	$0$	$0$	$0$	$1$
	$2$	$1$	$1$	$0$	$0$	$0$	$2$
	$3$	$1$	$3$	$1$	$0$	$0$	$5$
	$4$	$1$	$7$	$5$	$1$	$0$	$15$
	$5$	$1$	$15$	$25$	$10$	$1$	$52$

Bron uitwerking inclusief tabel: Lance Bakker

Opgave 447 ^[ooO]

Noem de persoon waar de leider mee begint $1$ en nummer zo alle mensen door tot en met $360$. Merk op dat de leider altijd de hoeden laat verwisselen in volgorde van $1, 2, \dots, 360, 1, 2, \dots, 360,\dots$, ongeacht de keuze voor $n$. Na elke beurt kunnen we per persoon opschrijven hoe vaak die persoon zijn of haar hoed heeft verwisseld. Als en alleen als deze $360$ getallen allemaal oneven zijn, heeft iedereen blauwe hoed op, want als en alleen als iemand zijn of haar hoed een oneven aantal keer heeft verwisseld, heeft diegene een blauwe hoed op. Omdat de leider altijd de hoeden laat verwisselen in vaste volgorde rond de cirkel, kunnen we stellen dat deze $360$ getallen dan ook gelijk moeten zijn aan elkaar. Anders zouden de getallen van twee mensen immers onderling minstens $2$ van elkaar verschillen, hetgeen impliceert dat de leider een verschillend aantal keer de cirkel $1, 2, \dots, 360$ af heeft gemaakt. Ten eerste is het natuurlijk mogelijk voor alle delers van $360$. Dan hoeft hij iedereen maar $1$ maal te vragen. Daarnaast geldt natuurlijk voor alle oneven getallen kleiner dan $360$. Als de leider dit oneven aantal beurten $360$ maal gehad heeft, is ieder persoon een oneven aantal keer van hoed verwisselt. Als derde is er nog een groep even getallen die delers zijn van oneven veelvouden van $360$. Dit zijn de getallen onder de $360$ die hoogstens $3$ priemfactoren $2$ hebben.

Opgave 448 ^[ooO]

In de figuur hieronder hebben we de de 7 trap verdeeld in 16 witte en 12 grijze vakjes. Als we de 7 trap moeten vullen met 6 dezelfde tetromino’s is de enige optie de T- tetromino. De andere tetromino’s hebben evenveel witte als grijze vlakjes. Dat zou betekenen dat de zevende tetromino alleen 4 witte vlakjes zou mogen hebben maar dat is onmogelijk.

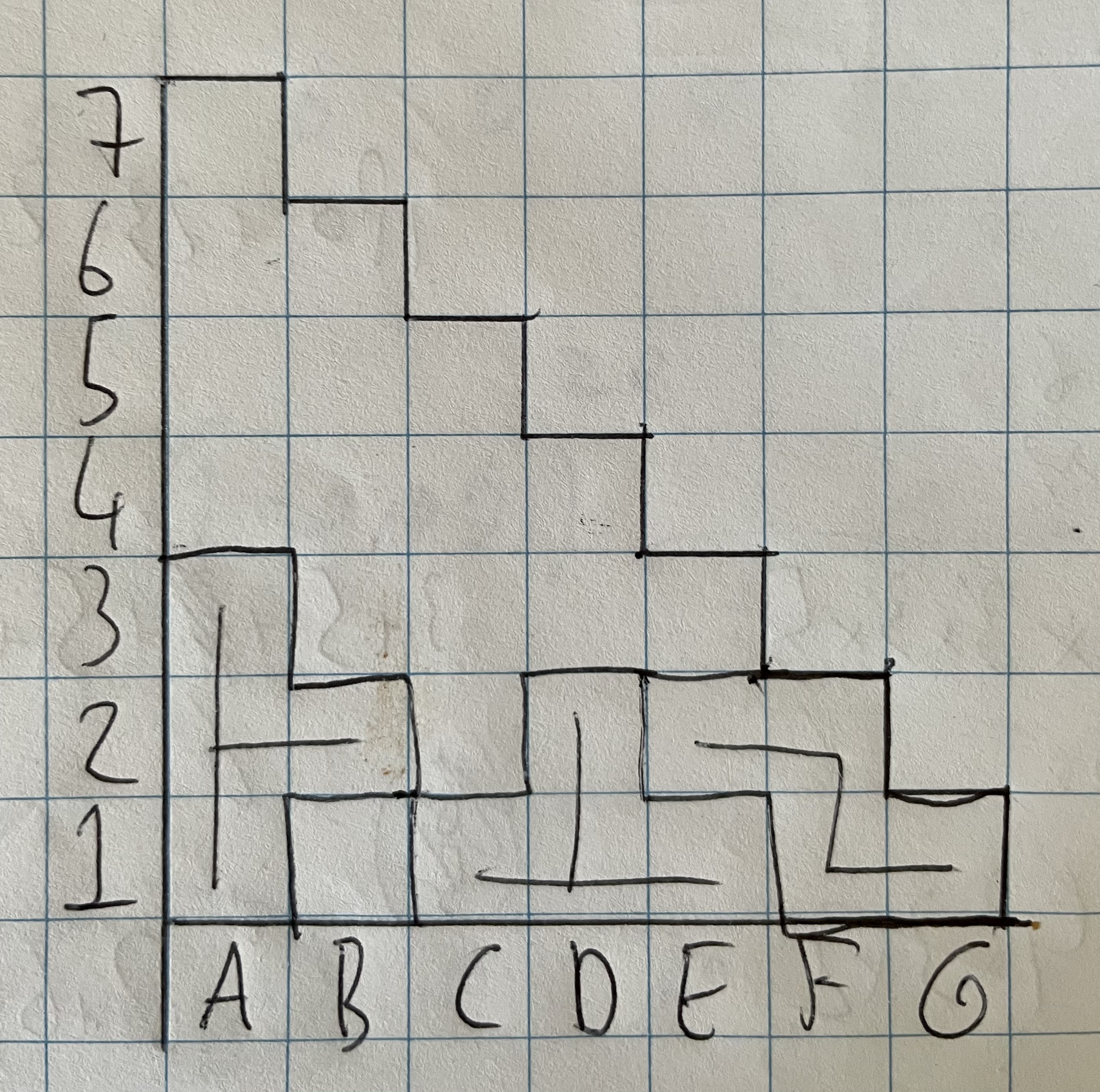
S-tetromino

Stel je voor dat we als zevende tetromino de S-tetromino gebruiken. Als we de S-tetromino op $(G1,F1,F2,E2)$ leggen dan moeten we een T-tetromino op $(E1,D1,C1,D2)$ leggen en een T-tetromino op $(A1,A2,A3,B2)$. Maar nu blijft $B1$ gedwongen leeg. Een tegenspraak dus. Dit betekent dat een T-tetromino op $G1$ moet liggen en een T-tetromino op $A7$. Bekijk nu $E3$. Dit vakje moet wel gevuld worden door de S-tetromino, want als die gevuld zou zijn door een T-tetromino, dan kan $E2$ niet meer gevuld worden (met $(E3,D3,C3,D2)$ of $(E3,D3,D4,D2)$) of kunnen $B5$, $C5$ en $C4$ niet tegelijk gevuld worden (met $(E3,D3,C3,D4)$: $C5$ kan niet gevuld worden door een S-tetromino zonder dat $B5$ of $C4$ onvulbaar worden en uberhaupt niet gevuld worden door een T-tetromino), tegenspraak. Vanwege symmetrie moet ook $C5$ gevuld worden door de S-tetromino, maar een S-tetromino kan niet zowel $E3$ als $C5$ vullen: we concluderen dat we geen S-tetromino als laatste kunnen kiezen.

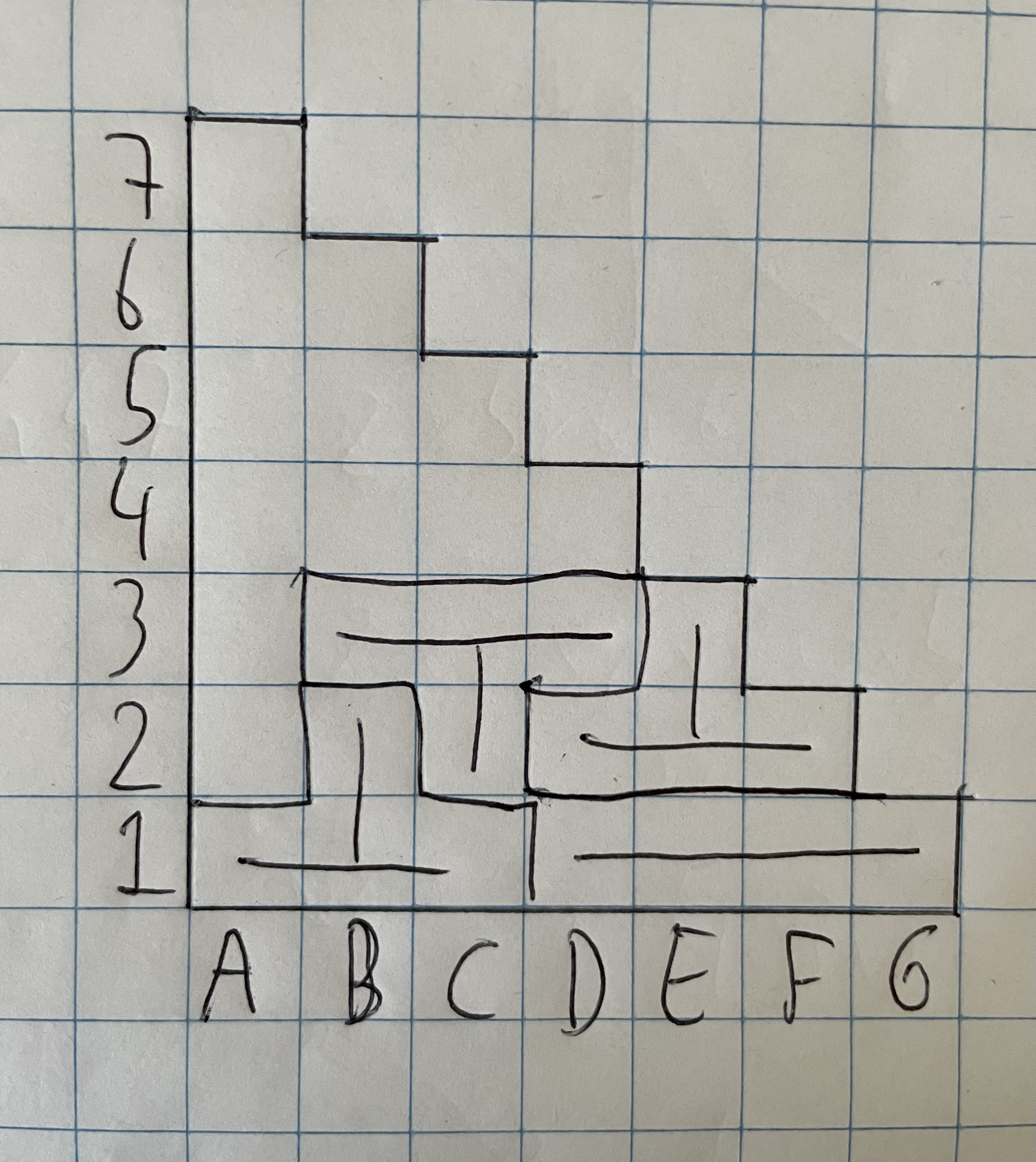
I-tetromino

Stel je voor dat we de I-tetromino als laatste nemen. We leggen deze tetromino op $(G1,F1,E1,D1)$. Dan leggen we een T-tetromino op $(A1,B1,C1,B2)$ en een T-tetromino op $(B3,C3,D3,C2)$ en een T-tetromino op $(D2,E2,F2,E3)$. Maar nu blijft $A2$ onbezet. Een tegenspraak dus. Dit betekent dat we een T-tetromino op $G1$ en $A7$ moeten plaatsen. Hierdoor kunnen we niet meer op D4 een I-tetromino plaatsen. Maar ook geen T-tetromino, want als we bijvoorbeeld een $(D4,D3,E3,C3)$-tetromino plaatsen, is het onmogelijk om de I-tetromino ergens te plaatsen zonder dat er onvervulbare vakjes ontstaan voor de T-tetromino’s.

L-tetromino

Stel je voor dat we een L-tetromino als laatste nemen. Maar dan geldt alweer dat $A7$ en $G1$ gevuld moeten worden door T-tetromino’s (want $(A7,A6,A5,B5)$ levert een geïsoleerde $B6$ op en op vergelijkbare manier kan ook $G1$ niet gevuld worden door een L-tetromino). Net als de vorige gevallen geldt vervolgens dat $D4$ niet gevuld kan worden door een L-tetromino, noch door een T-tetromino. (Een L-tetromino laat zo steeds ofwel $C5$, ofwel $E3$ onvervulbaar, en een T-tetromino iets indirecter ook, omdat dan een aangrenzend vakje aan $C5$ of $E3$ wordt opengelaten als we die vullen: precies dezelfde logica als de gevallen hierboven.

O-tetromino

Stel je als laatste voor dat we de O-tetromino als laatste tetromino nemen. Dan moeten $A7$ en $G1$ in ieder geval gevuld worden door een T-tetromino (door een O-tetromino kan niet) met maar 1 plaatsingsmogelijkheid: zie het plaatje hieronder. Beschouw nu vakje $E3$. Als die gevuld wordt door een O-tetromino op $(E3,E2,D2,D3)$, dan moet $D1$ gevuld worden door een $(B1,C1,D1,C2)$-tetromino. $A1$ moet dan gevuld worden door een $(A1,A2,A3,B2)$-tetromino, et cetera tot we een geldige vulling krijgen: figuur hieronder. Als $E3$ daarentegen niet gevuld wordt door een O-tetromino, moet die wel gevuld worden door een $(E3,D3,C3,D4)$-tetromino (de andere configuraties voor de T-tetromino laten $E2$ open en onvulbaar). $C5$ moet dan gevuld worden door een O-tetromino en we krijgen zodoende een spiegeling van de figuur hieronder: