Opgave 477 ^[oOO]

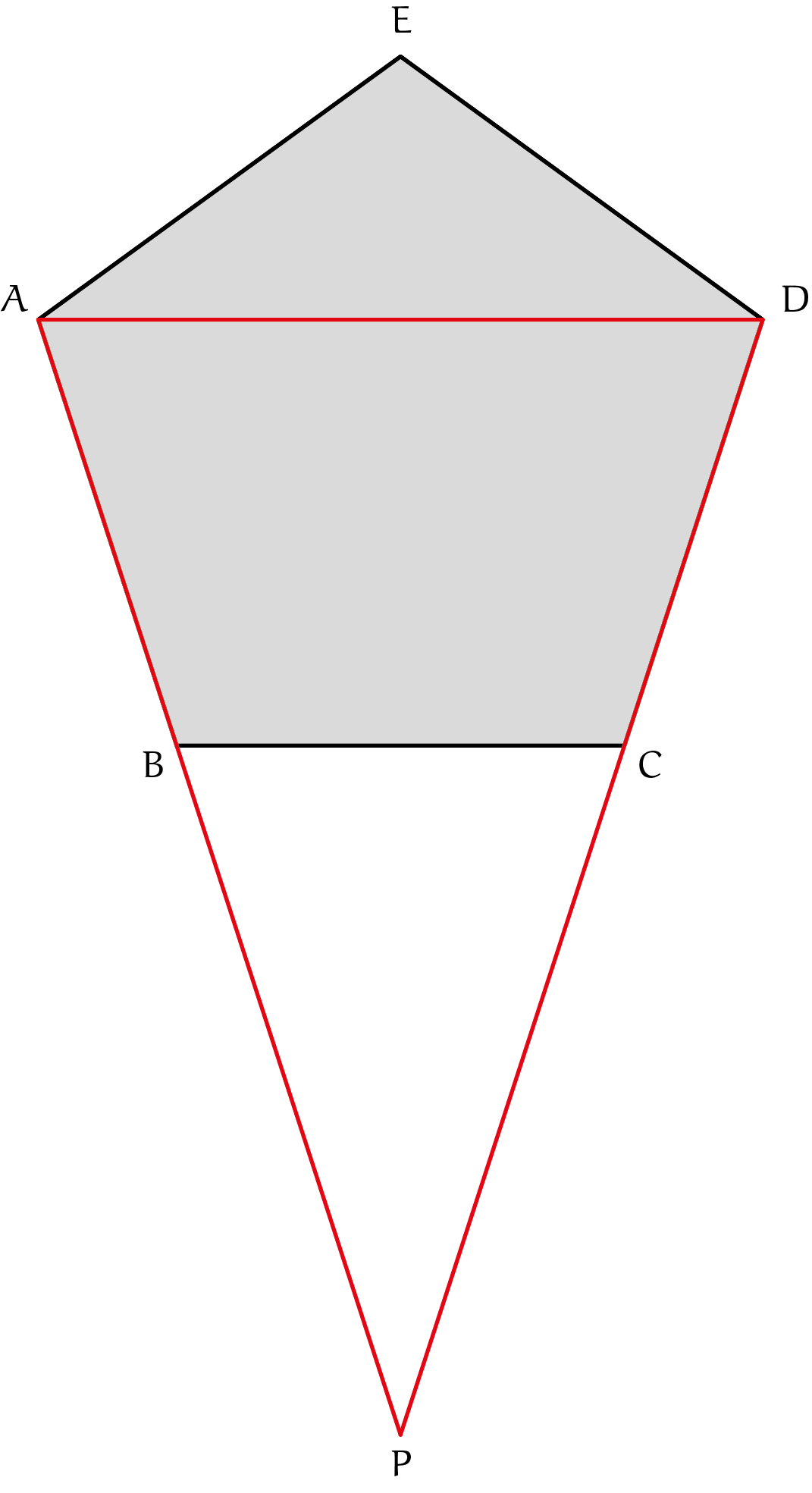
Noem de zijde van de regelmatige vijfhoek even $s$. We beweren dat de omtrek van de rode driehoek langer is dan die van de vijfhoek, welke gelijk is aan $5s$. Om dit in te zien, merken we op dat de omtrek van de rode driehoek gelijk is aan
$$|AB| + |BP| + |PC| + |CD| + |DA| = 2s + |BP| + |PC| + |AD|.$$

Als we nu kunnen laten zien dat elk van $|BP|$, $|PC|$ en $|AD|$ langer is dan $s$, dan zijn we klaar. Omdat $\angle DPB = 36^{\rm o} = \angle PDB$ volgt dat $\triangle DPB$ gelijkbenig is met top $B$ en zo volgt dat $|BP|  = |BD|$. Dit is een van de diagonalen van de vijfhoek. Geheel analoog volgt dan dat $|BP| = |PC| = |AD| > s$ omdat de diagonalen van de vijhoek zeker langer zijn dan zijn zijden.

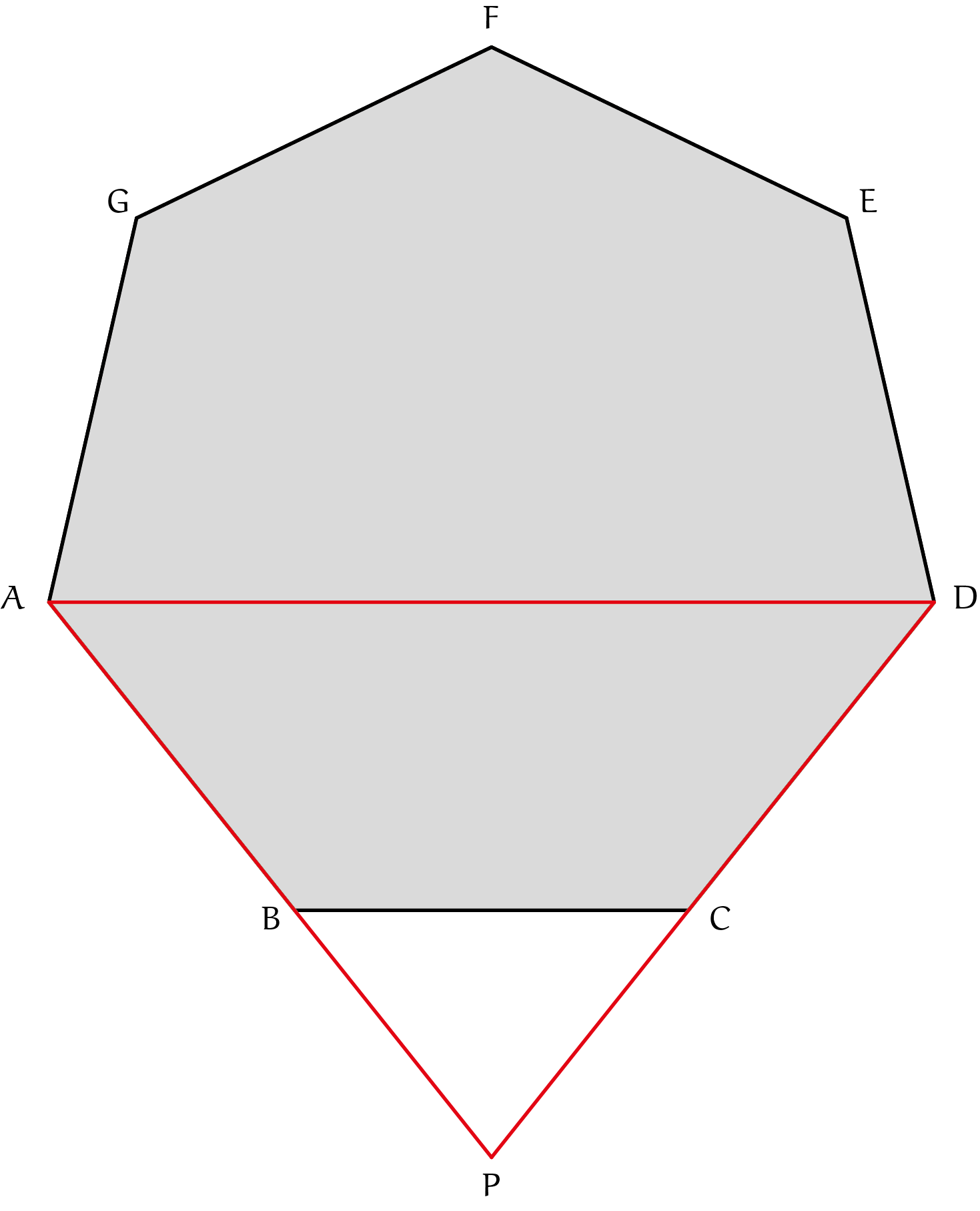
Anderzijds beweren we dat de omtrek van de zevenhoek, gelijk aan $7s$, groter is dan die van de driehoek, welke gelijk is aan
$$|AB| + |BP| + |PC| + |CD| + |DA| = 2s + |BP| + |PC| + |AD|.$$
Inderdaad, middels de driehoeksongelijkheid volgt dat
$$|AD| < |AB| + |BC| + |CD| = 3s,$$
dus het volstaat om aan te tonen dat $|BP| = |PC|$ korter is dan $s$. Dit volgt uit het feit dat $\angle BPC > 60^{\rm o}$ en daarmee is het de grootste hoek in $\triangle BPC$. Hiermee is zijde $|BC|$ ook de langste zijde in $\triangle BPC$. 

Opgave 478 ^[oOO]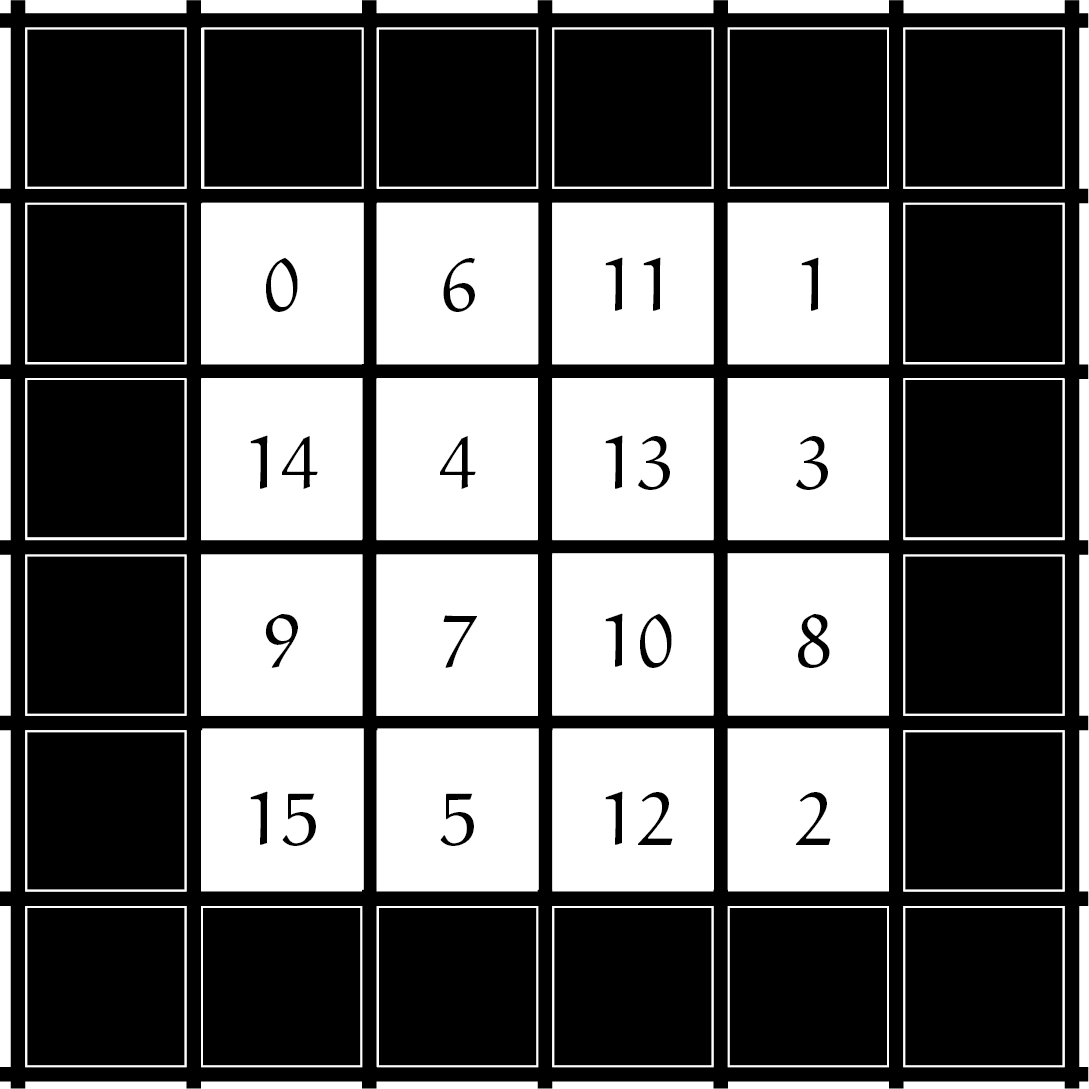

Ja, dit is mogelijk. Een voorbeeld is hiernaast weergegeven; door de getallen in volgorde te doorlopen vindt men een pad dat aan de volwaarden van de opgave voldoet.

Opgave 479 ^[ooO]

Dit is opnieuw mogelijk; neem bijvoorbeeld

$$x^3 + 6x^2 - 135x = x(x-9)(x+15).$$

De afgeleide hiervan is gelijk aan

$$3x^2 + 12x - 135 = 3(x-5)(x+9).$$

Opgave 480 ^[ooO]

Zij $D$ de projectie van $C$ op $AB$. Allereerst volgt dat $\triangle ADC$ gelijkbenig is met top $D$ en zodoende $|AD| = |DC|$. We zien verder dat $\triangle BCD$ een halve gelijkzijdige driehoek is, waarmee $|DC| = |CM|$. Omdat $\angle DCM = 60^{\rm o}$, volgt hieruit zelfs dat $\triangle DCM$ gelijkzijdig is, waarmee $|DC| = |DM|$. We concluderen dat $|AD| = |DC| = |DM|$; oftewel, $\triangle ADM$ is gelijkbenig met top $D$. Daar $\angle BDM = \angle DBM = 30^{\rm o}$, volgt hieruit dat $\angle BAM = 15^{\rm o}$, zoals verlangd.

Voor de bonus merken we op dat per definitie van $P$ geldt dat $\triangle AMB \sim \triangle BMP$. Hieruit volgt dat
\[
\frac{|AM|}{|CM|} = \frac{|AM|}{|BM|} = \frac{|BM|}{|PM|} = \frac{|CM|}{|PM|}.
\] 
Gecombineerd met de gemeenschappelijke ingesloten hoek $\angle AMC = \angle CMP$ volgt hieruit dat $\triangle AMC \sim \triangle CMP$. In het bijzonder volgt dat $\angle PCM = \angle CAM = 30^{\rm o}$.