
Pythagoras Olympiade 61-6, juni 2022
Opgave 477 [oOO]
Hieronder zijn een regelmatige vijfhoek en zevenhoek weergegeven. Aan de hand van beide figuren is een rode driehoek getekend. Heeft de rode driehoek in de vijfhoek een langere omtrek dan de vijfhoek zelf? En hoe zit het met de rode driehoek in de zevenhoek?
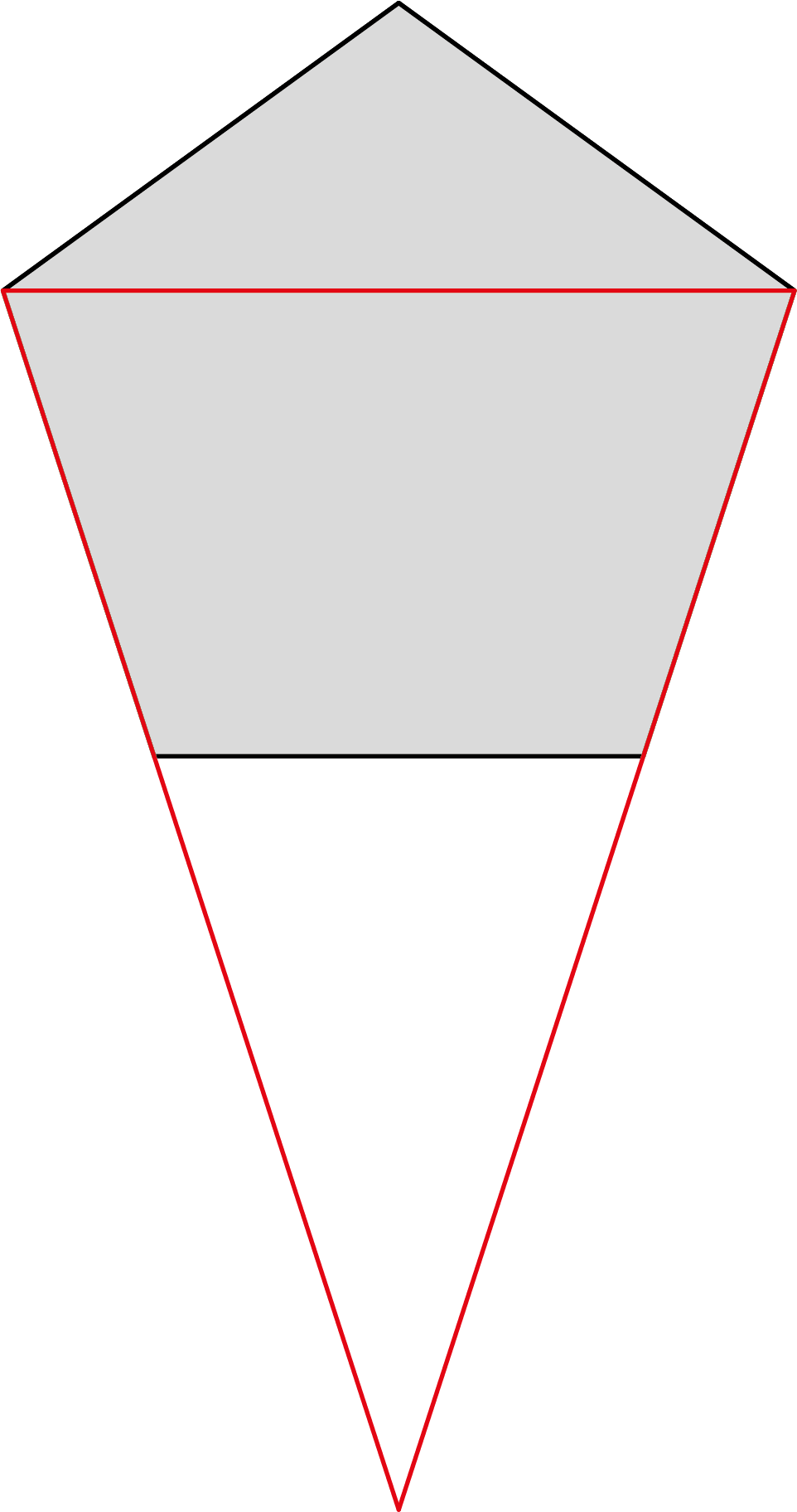 |
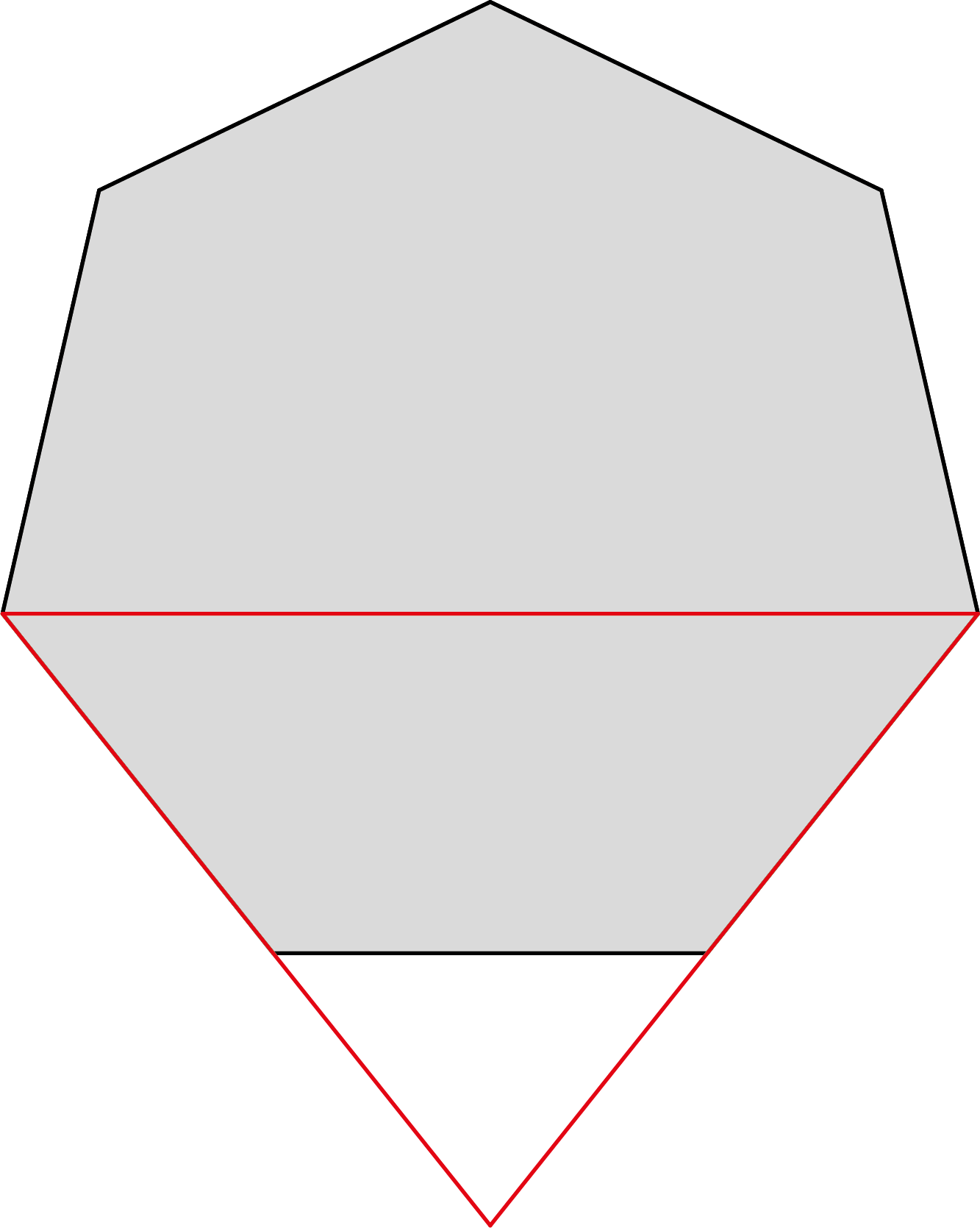 |
 Opgave 478 [oOO]
Opgave 478 [oOO]
We spelen een spel op een $4\times 4$ bord, waarbij we enkel horizontale en verticale sprongen mogen maken van $2$ en $3$ vakjes; zie de afbeelding voor een voorbeeld, waarin we alleen de rode vakjes bezoeken.
Is het mogelijk om middels een aantal sprongen elk vakje precies eenmaal te bezoeken, alvorens weer terug te keren naar het beginvakje?
Opgave 479 [ooO]
Bepaal of er een functie $f$ van de vorm $x^3 + ax^2 + bx + c$ bestaat met $a$, $b$, $c$ gehele getallen die voldoet aan de volgende eigenschappen:
- de oplossingen van de vergelijking $f(x) = 0$ zijn drie verschillende gehele getallen;
- de oplossingen van de vergelijking $f'(x) = 0$ zijn twee verschillende gehele getallen.
Opgave 480 [ooO]
Zij $ABC$ een driehoek met $\angle A = 45^{\rm o}$ en $\angle B = 30{\rm o}$. Laat $M$ het midden van $BC$ zijn. Bewijs dat $\angle BAM = 15^{\rm o}$.
Bonus Zij nu $P$ het punt op $AM$ waarvoor $\angle ABP = 15^{\rm o}$. Bewijs dat $\angle PCM = 30^{\rm o}$.

