Opgave 517 ^[oOO]

Het vierkant heeft een oppervlakte van $1^2 = 1$. Noem $m$ de oppervlakte van het overlappende deel van het vierkant en de cirkel, $b$ de oppervlakte van het blauwe deel en $g$ de oppervlakte van het groene deel. Omdat de cirkel en het vierkant hetzelfde middelpunt hebben zijn de vier hoekstukjes die buiten de cirkel liggen even groot, en dus is de oppervlakte van het vierkant $m + 4b$. Met dezelfde redenatie is de oppervlakte van de cirkel $m + 4g$. Omdat gegeven is dat $b = g$ is ook $m + 4b = m + 4g$ en dus hebben de cirkel en het vierkant dezelfde oppervlakte. De oppervlakte van de cirkel is dus ook $1$. 

Opgave 518 ^[oOO]

Het is mogelijk om een lijst van alle kwadraten van drie en vier cijfers te maken, maar er is een andere manier om deze opgave aan te pakken. Laat $m$ het lievelingsgetal van Anique zijn en $n$ het lievelingsgetal van Berend. Merk op dat $n^2 - m^2 = ABBC - ABC$ op twee nullen eindigt en dus deelbaar is door $100$. Dus $n^2 - m^2$ is deelbaar door 4 en door 25. Omdat het deelbaar is door 4 moeten $m$ en $n$ beiden even of beiden oneven zijn. Omdat het deelbaar is door 25, geldt dat

$$25 \mid (n + m)(n - m)$$

waarna er drie mogelijke conclusies zijn:

1. $5 \mid n + m, n - m$. 
2. $25 \mid n - m$
3. $25 \mid n + m$

In het eerste geval volgt dat $m$ en $n$ allebei deelbaar zijn door $5$. De enige waarde voor $m$ zodat $m^2 = ABC$ drie verschillende cijfers heeft is dan $m = 25$, maar 6225 is helaas geen kwadraat: deze mogelijkheid valt dus af. 

In het tweede geval volgt uit het feit dat $m$ en $n$ hetzelfde teken hebben dat $50 \mid m - n$. Omdat $m, n < 100$ is $n - m < 100$ dus $n - m = 50$. Merk op dat $n^2 - 10m^2 = ABBC - ABC0 = BC - C0$, en dit is het verschil tussen twee getallen van twee cijfers en ligt dus tussen de $-100$ en $100$. Op basis hiervan kunnen we een schatting van $m$ maken:

	$-100$	$<$	$n^2 - 10m^2 < 100$
	$-100$	$<$	$(m + 50)^2 - 10m^2 < 100$
	$-100$	$<$	$-9m^2 + 100m + 2500 < 100$.

Dit is een kwadratische ongelijkheid. Om deze op te lossen berekenen we eerst aan beide kanten het gelijkheidsgeval met de abc-formule. Voor de linker ongelijkheid lossen we $-100 = -9m^2 + 100m + 2500$ op:

$$m = \frac{10}{9}(5 - \sqrt{259}) \approx -12{,}32 \vee m = \frac{10}{9}(5 + \sqrt{259}) \approx 23{,}44.$$

Als $m = 0$ (wat tussen de twee oplossing in ligt) dan klopt de ongelijkheid, dus $m$ ligt tussen de twee oplossingen in. Dus $-12.32 < m < 23.44$, maar omdat $m$ sowieso al positief is is alleen de grens $m < 23{,}44$ relevant. Nu de rechter ongelijkheid. We lossen $-9m^2 + 100m + 2500 = 100$ op:

$$m = \frac{10}{9}(5 - \sqrt{241}) \approx -11{,}69 \vee m = \frac{10}{9}(5 + \sqrt{241}) \approx 22{,}80.$$

Als $m = 0$ (tussen de twee oplossingen in) dan klopt de ongelijkheid niet, dus $m$ ligt niet tussen de twee oplossingen in. Dus $m < -11{,}69$ of $m > 22{,}80$, maar omdat $m$ positief is vervalt het eerste geval. We concluderen dus dat $22{,}80 < m < 23{,}44$. Dan blijft $m = 23$ als enige mogelijkheid over. Dan zou $n = 73$, maar dan $n^2 = 5329$ en $m^2 = 529$ en dat voldoet helaas niet. 

Omdat de eerste twee mogelijkheiden nog niet tot een oplossing hebben geleid moet gelden dat $25 \mid n + m$. Omdat $n$ en $m$ hetzelfde teken hebben volgt dat $50 \mid n + m$. Omdat $m \leq 31$ (omdat $m^2$ drie cijfers heeft) en $n < 100$ geldt $n + m < 150$ en dus is $n + m$ gelijk aan 50 of 100. Als het $50$ is, dan vinden we omdat $m \geq 10$ dat $n \leq 40$, dus $n^2 \leq 1600$. Dit is niet van de vorm $ABBC$ dus $n^2 < 1600$, dus $m^2 < 160$ en dus $m \leq 12$. Voor $m = 12$ vinden we $n = 38$ en dus $m^2 = 144, n^2 = 1444$, maar omdat $B$ en $C$ dan niet verschillend zijn vervalt deze oplossing. Ook $11^2 = 121$ en $10^2 = 100$ bestaan niet uit drie verschillende cijfers en vallen dus af. Dus $n + m = 50$ is niet mogelijk, en dus $n + m = 100$. Net als in het vorige geval geldt $-100 < n^2 - 10m^2 < 100$, en nu geeft dat

	$-100$	$<$	$(100 - m)^2 - 10m^2 < 100$
	$-100$	$<$	$-9m^2 - 200m + 10000 < 100$.

Weer berekenen we aan beide kanten het gelijkheidsgeval met dezelfde techniek als eerst. De linker ongelijkheid geeft

$$m = \frac{10}{9}(-10 - \sqrt{1009}) \approx -46{,}41 \vee m = \frac{10}{9}(-10 + \sqrt{1009}) \approx 24{,}18$$

en $m = 0$ invullen geeft een kloppende ongelijkheid dus $-46{,}41 < m < 24{,}18$. De rechter ongelijkheid geeft

$$m = \frac{10}{9}(-10-\sqrt{991}) \approx -46{,}09 \vee m = \frac{10}{9}(-10+\sqrt{991}) \approx 23{,}87$$

en nu geeft $m = 0$ geen kloppende ongelijkheid dus $m < -46{,}09$ of $m < 23{,}87$. Omdat $m$ positief is vinden we $23{,}87 < m < 24{,}18$ dus $m = 24$. Dan $n = 76$ en dit geeft $n^2 = 5776$ en $m^2 = 576$. Dit zijn dus de lievelingsgetallen van Anique en Berend. 

Opgave 519 ^[ooO]

Ook deze opgave is op te lossen door alle mogelijke tijden uit te schrijven, maar het is vlotter te doen door gevalsonderscheiding te doen voor $A$ en $C$, omdat deze maar vrij weinig waarden kunnen aannemen. $A$ ligt altijd tussen $0$ en $2$, en $C$ altijd tussen $0$ en $5$. Laten we beginnen:

• $A = C = 0$. Dan reduceert $A + B + C + D = A \cdot B + C \cdot D$ tot $B + D = 0$, en we vinden hiermee $\color{red}{1}$ oplossing $B = D = 0$. 
• $A = 0, C = 1$. Dan reduceert $A + B + C + D = A \cdot B + C \cdot D$ tot $B + D + 1 = D$. Dit geeft geen oplossingen.
• $A = 0, C = 2$. Dan reduceert $A + B + C + D = A \cdot B + C \cdot D$ tot $B + D + 2 = 2D$. Dus $B + 2 = D$. Dit geeft $\color{red}{8}$ oplossingen. 
• $A = 0, C = 3$. Dan reduceert $A + B + C + D = A \cdot B + C \cdot D$ tot $B + D + 3 = 3D$, dus $B + 3 = 2D$. Dit geeft $\color{red}{5}$ oplossingen $(B, D) = (1, 2), (3, 3), (5, 4), (7, 5), (9, 6)$. 
• $A = 0, C = 4$. Dan reduceert $A + B + C + D = A \cdot B + C \cdot D$ tot $B + D + 4 = 4D$, dus $B + 4 = 3D$. Dit geeft $\color{red}{3}$ oplossingen $(B, D) = (2, 2), (5, 3), (8, 4)$. 
• $A = 0, C = 5$. Dan reduceert $A + B + C + D = A \cdot B + C \cdot D$ tot $B + D + 5 = 5D$, dus $B + 5 = 4D$. Dit geeft $\color{red}{2}$ oplossingen $(B, D) = (3, 2), (7, 3)$. 
• $A = 1, C = 0$. Dan reduceert $A + B + C + D = A \cdot B + C \cdot D$ tot $B + D + 1 = B$, en dit heeft geen oplossingen. 
• $A = 1, C = 1$. Dan reduceert $A + B + C + D = A \cdot B + C \cdot D$ tot $B + D + 2 = B + D$, en dit heeft geen oplossingen. 
• $A = 1, C = 2$. Dan reduceert $A + B + C + D = A \cdot B + C \cdot D$ tot $B + D + 3 = B + 2D$, dus $D = 3$. $B$ is dan een vrije variabele en kan dus alle waarden $B = 0, 1, \ldots 9$ aannemen: we vinden dus $\color{red}{10}$ oplossingen. 
• $A = 1, C = 3$. Dan reduceert $A + B + C + D = A \cdot B + C \cdot D$ tot $B + D + 4 = B + 3D$, dus $2D = 4$, dus $D = 2$. $B$ is dan een vrije variabele, we vinden dus $\color{red}{10}$ oplossingen. 
• $A = 1, C = 4$. Dan reduceert $A + B + C + D = A \cdot B + C \cdot D$ tot $B + D + 5 = B + 4D$, dus $3D = 5$, maar dit heeft geen oplossingen. 
• $A = 1, C = 5$. Dan reduceert $A + B + C + D = A \cdot B + C \cdot D$ tot $B + D + 6 = B + 5D$, dus $4D = 6$, maar dit heeft geen oplossingen. 
• $A = 2, C = 0$. Dan reduceert $A + B + C + D = A \cdot B + C \cdot D$ tot $B + D + 2 = 2B$, dus $D + 2 = B$. Omdat in dit geval $0 \leq B \leq 3$ ($AB$ is maximaal 23) vinden we zo $\color{red}{2}$ oplossingen. 
• $A = 2, C = 1$. Dan reduceert $A + B + C + D = A \cdot B + C \cdot D$ tot $B + D + 3 = 2B + D$, dus $B = 3$. $D$ is vrij en dit geeft dus $\color{red}{10}$ oplossingen. 
• $A = 2, C = 2$. Dan reduceert $A + B + C + D = A \cdot B + C \cdot D$ tot $B + D + 4 = 2B + 2D$, dus $B + D = 4$. Dit heeft $\color{red}{4}$ oplossingen (omdat $B = 4$ niet mogelijk is).
• $A = 2, C = 3$.  Dan reduceert $A + B + C + D = A \cdot B + C \cdot D$ tot $B + D + 5 = 2B + 3D$, dus $B + 2D = 5$. Dit geeft $\color{red}{2}$ oplossingen $(B, D) = (1, 2), (3, 1)$. 
• $A = 2, C = 4$. Dan reduceert $A + B + C + D = A \cdot B + C \cdot D$ tot $B + D + 6 = 2B + 4D$, dus $B + 3D = 6$. Dit geeft $\color{red}{2}$ oplossingen $(B, D) = (0, 2), (3, 1)$. 
• $A = 2, C = 5$. Dan reduceert $A + B + C + D = A \cdot B + C \cdot D$ tot $B + D + 7 = 2B + 5D$, dus $B + 4D = 7$. Dit geeft $\color{red}{1}$ oplossing $(B, D) = (3, 1)$.

In totaal vinden we dus $1 + 8 + 5 + 3 + 2 + 10 + 10 + 2 + 10 + 4 + 2 + 2 + 1 = 60$ oplossingen. Het is nog steeds redelijk wat werk, maar veel minder dan als we alle oplossingen zouden uitschrijven, en bovendien een stuk minder foutgevoelig. 

Opgave 520 ^[ooO]

Laat $r$ de straal zijn van cirkels $A, B, C$ en $D$. Een cirkel kan op 8 manieren aan cirkels $B, C$ en $D$ raken: bij alle cirkels namelijk in- of uitwendig. De meeste van deze cirkels raken echter altijd ook aan cirkel $A$. De enige twee mogelijkheden die niet automatisch aan $A$ raken zijn de rode en groene cirkel in het plaatje. De crux is dat de groene cirkel van kromming wisselt naarmate $r$ groter wordt, en er is dus precies een waarde $r$ waarvoor deze cirkel een rechte lijn wordt. Het is voor deze waarde van $r$ dat er maar een unieke cirkel is die aan de eisen voldoet, namelijk de rode cirkel. Credits naar Marcel Roggeband voor het mooie plaatje.

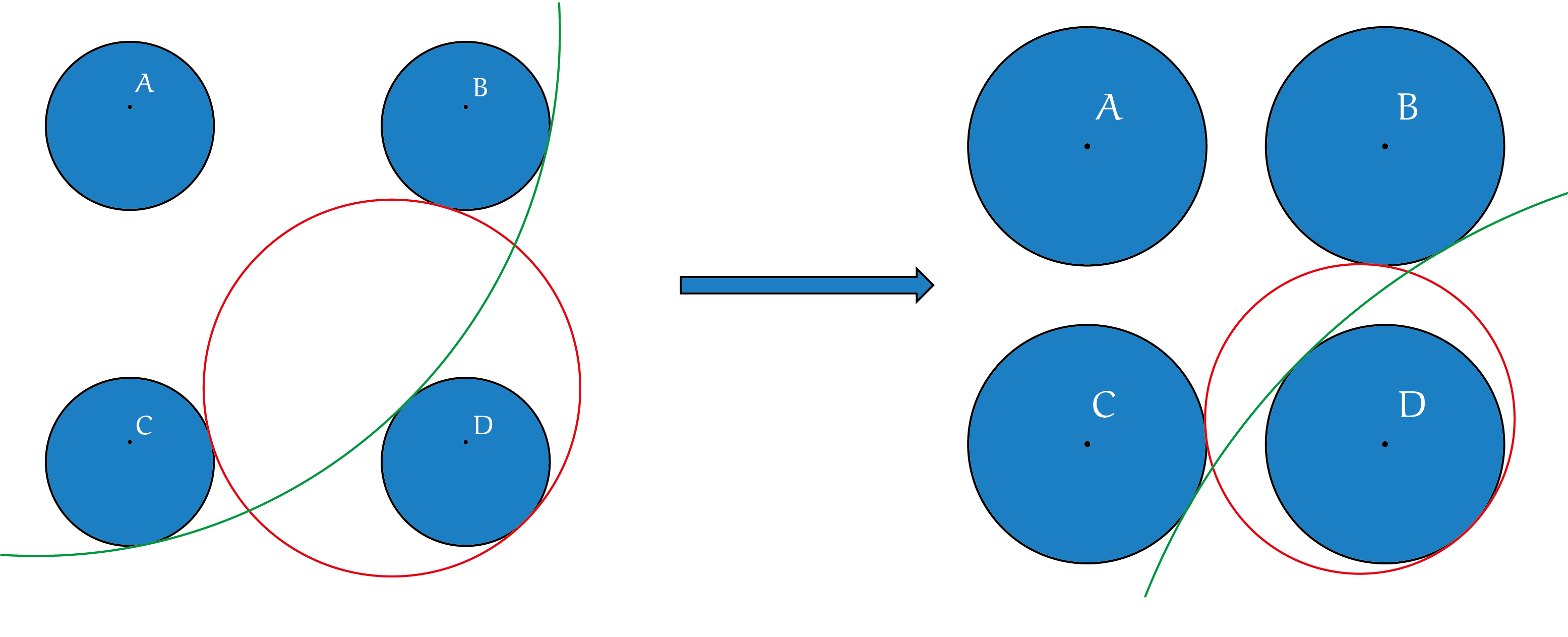
De opgave is dus het vinden van de straal $r$ zodat de groene cirkel een rechte lijn wordt. Laten we nog een plaatje maken van deze situatie:

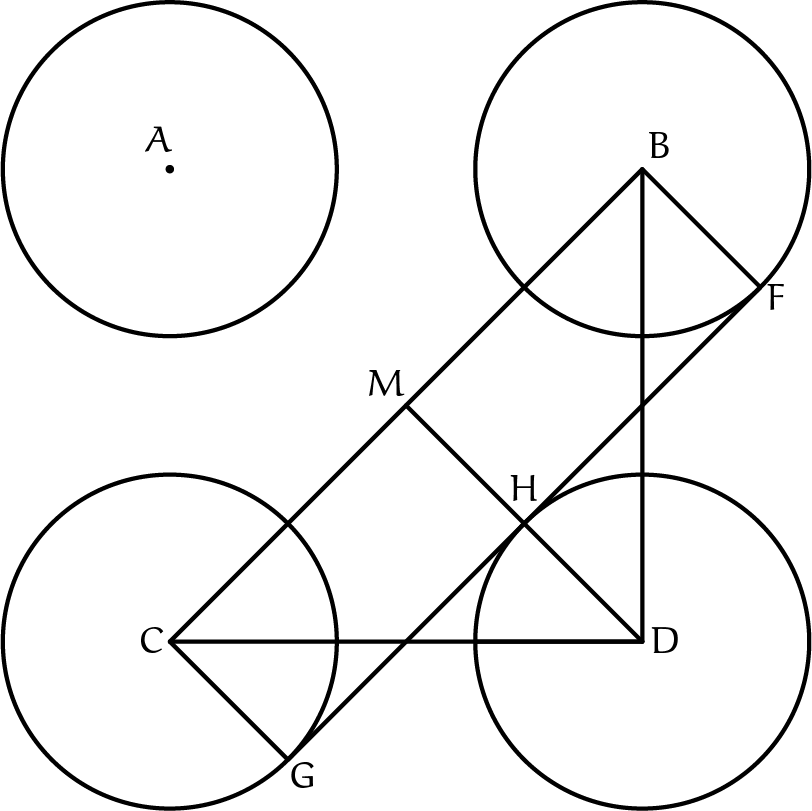
Hier zijn $F, G, H$ de raakpunten van de gemeenschappelijke raaklijn (de groene cirkel in het vorige plaatje) met de drie cirkels $B, C, D$. Verder is $M$ het snijpunt van $HD$ met de lijn $BC$ (merk op, we mogen nog niet gebruiken dat $A$ ook op $HD$ ligt!). Een raaklijn staat altijd loodrecht op een lijn door het middelpunt van de cirkel, dus $CG \perp GF \perp BF$. Hieruit volgt $BF \parallel CG$. Omdat $|BF| = |CG| = r$ is $BCGF$ een vierhoek en een tweetal parallelle, even lange zijden, en dus een parallellogram. Omdat $\angle BFG = 90^\circ$ is het een parallellogram met een rechte hoek, dus een rechthoek. Omdat $\angle GHD = 90^\circ$ is $\angle GHM = 90^\circ$ en dus is $CGHM$ ook een rechthoek, dus $\angle DMC = 90^\circ$. Omdat $\angle MCD = \angle BCD = 45^\circ$ is $\triangle MCD \sim \triangle DBC \, (hh)$. Dus is

$$\frac{|MD|}{|DC|} = \frac{|DC|}{|CB|} \Longrightarrow \frac{|MD|}{12} = \frac{12}{12\sqrt{2}} \Longrightarrow |MD| = 6\sqrt{2}$$

Merk op dat $|MD| = |MH| + |HD|$. Nu is $|HD| = r$ per definitie, en $|MH| = |CG|$ omdat $MHGC$ een rechthoek is, dus $|MH| = r$. Dus $|MD| = r + r = 2r$, dus $2r = 6\sqrt{2}$. We concluderen dat $r = 3\sqrt{2}$ de gevraagde straal is van de vier cirkels.