Inzenden kon tot uiterlijk 20 april 2024

Opgave 517 ^[oOO]

In onderstaande afbeelding hebben de cirkel en het vierkant hetzelfde middelpunt. De zijde van het vierkant is gelijk aan 1 en de oppervlaktes van het groene en het blauwe gebied zijn gelijk. Wat is de oppervlakte van de cirkel?

Opgave 518 ^[oOO]

Anique en Berend hebben beiden een lievelingsgetal. Als Anique het kwadraat van haar lievelingsgetal uitrekent, is het van de vorm $ABC$ voor drie verschillende cijfers $A \neq 0$, $B$ en $C$. Als Berend ook van zijn lievelingsgetal het kwadraat uitrekent, blijkt het precies het getal $ABBC$ te zijn. Wat zijn de lievelingsgetallen van Anique en Berend?

Opgave 519 ^[ooO]

Op een digitale 24-uursklok verschijnen tijdstippen van de vorm $AB:CD$. Voor hoeveel tijdstippen geldt dagelijks dat $A + B + C + D = A \cdot B + C \cdot D$?

Opgave 520 ^[ooO]

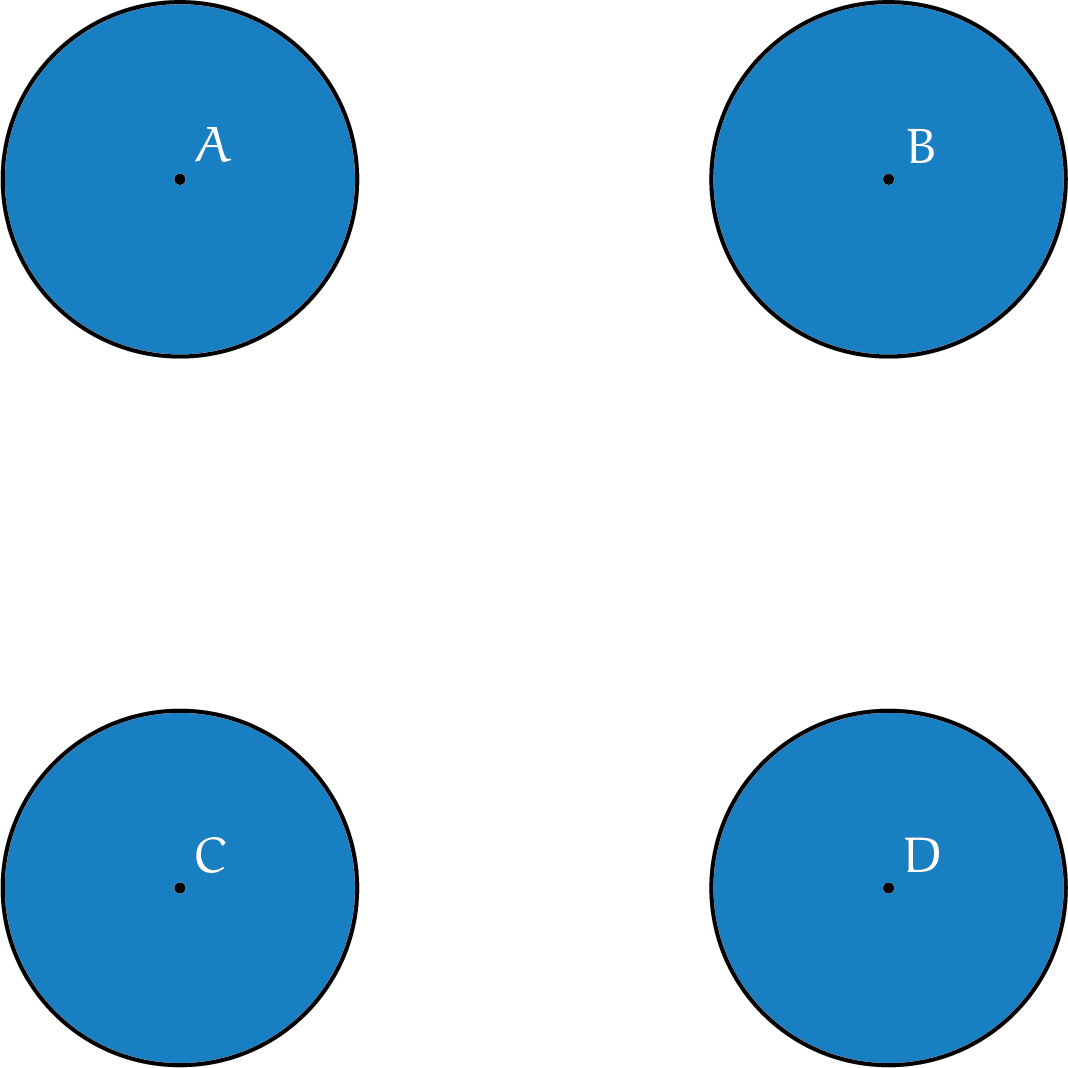
Cirkels kunnen elkaar op twee manieren raken: inwendig of uitwendig. Hieronder zie je vier congruente cirkels $A$, $B$, $C$ en $D$ die elkaar niet raken of overlappen. De middelpunten zijn hoekpunten van een vierkant met zijde $12$. Er bestaat precies één vijfde cirkel die wel de cirkels $B$, $C$ en $D$ (inwendig of uitwendig) raakt, maar niet cirkel $A$. Hoe groot is de straal van de vier cirkels $A$, $B$, $C$ en $D$? (De verhoudingen zijn niet correct getekend).

Met dank aan Huub Odijk.

 

Bekijk oplossing