Oplossingen Pythagoras Olympiade 64-1
Opgave 529 [oOO]
We beschouwen in deze uitwerking het getal nul niet als zijnde een “getal onder de 1000”; we beschouwen enkel positieve gehele getallen. We doen nu de volgende observaties:
- Een getal met som van de cijfers gelijk aan 1 mag (naast nullen) enkel een 1 hebben; hiervoor zijn dus $3$ mogelijkheden.
- Een getal met som van de cijfers gelijk aan 2 mag (naast nullen) ofwel een 2 hebben, ofwel twee 1en. Hiervoor zijn dan $3 + 3 = 6$ mogelijkheden.
- Een getal met som van de cijfers gelijk aan 3 mag (naast nullen) ofwel een 3 hebben, ofwel een 2 en een 1, ofwel drie 1en. Hiervoor zijn dan $3 + 6 + 1 = 10$ mogelijkheden.
- Een getal met som van de cijfers gelijk aan 4 mag (naast nullen) ofwel een 4 hebben, ofwel een 3 en een 1, ofwel twee 2en, ofwel een 2 en twee 1en. Hiervoor zijn dan $3 + 6 + 3 + 3 = 15$ mogelijkheden.
- Een getal met som van de cijfers gelijk aan 5 mag (naast nullen) ofwel een 5 hebben, ofwel een 4 en een 1, ofwel een 3 en een 2, ofwel een 3 en twee 1en, ofwel twee 2en en een 1. Hiervoor zijn dan $3 + 6 + 6 + 3 + 3 = 21$ mogelijkheden.
- Een getal met som van de cijfers gelijk aan 6 mag (naast nullen) ofwel een 6 hebben, ofwel een 5 en een 1, ofwel een 4 en een 2, ofwel een 4 en twee 1en, ofwel twee 3en, ofwel een 3 en een 2 en een 1, ofwel drie 2en. Hiervoor zijn dan $3 + 6 + 6 + 3 + 3 + 6 + 1 = 28$ mogelijkheden.
- Een getal met som van de cijfers gelijk aan 7 mag (naast nullen) ofwel een 7 hebben, ofwel een 6 en een 1, ofwel een 5 en een 2, ofwel een 5 en twee 1en, ofwel een 4 en een 3, ofwel een 4 en een 2 en een 1, ofwel twee 3en en een 1, ofwel een 3 en twee 2en. Hiervoor zijn dan $3+6+6+3+6+6+3+3 = 36 $mogelijkheden.
We hebben nu in totaal al $3+6+10+15+21+28+36 = 119$ getallen gevonden; dat zijn er genoeg. Optimaal is dus om alle getallen te gebruiken met som van de cijfers hoogstens 6, en om de laatste $17$ getallen te kiezen met som van de cijfers 7. In totaal vinden we dan als som van alle cijfers
\begin{align*}
3 \cdot 1 + 6 \cdot 2 + & 10 \cdot 3 + 15 \cdot 4 + 21 \cdot 5 + 28 \cdot 6 + 17 \cdot 7 \\
&= 3 + 12 + 30 + 60 + 105 + 168 + 161 \\
&= 15 + 90 + 273 + 119 = 105 + 392 = 497.
\end{align*}
Opgave 530 [oOO]
We mogen zonder verlies van algemeenheid aannemen dat hoekpunt $A$ het bovenste hoekpunt is. In totaal zijn er dan nu nog $10 \cdot 9/2 = 45$ keuzes over voor het tweetal hoekpunten $B$ en $C$. Als een van deze hoekpunten, zeg $B$, direct naast $A$ ligt, dan is er maar $1$ keuze voor $C$ waarbij het middelpunt van de cirkel in de driehoek ligt. Als er precies $1$ hoekpunt tussen $A$ en $B$ in ligt, dan zijn er twee keuzes voor het hoekpunt $C$ waarbij dit gebeurt. Dit patroon zet zich voort; we vinden in totaal $1 + 2 + 3 + 4 + 5 = 15$ configuraties waarbij het middelpunt van de cirkel in de driehoek $ABC$ ligt. De kans dat dit gebeurt is derhalve $15/45 = 1/3$.
Opgave 531 [ooO]
We bewijzen, als $n-1$ niet deelbaar is door $3$, dat $7111\!\dots\!111$ dan ook geen priemgetal kan zijn. Stel daartoe eerst dat $n$ een drievoud plus $2$ is. Dan ziet men gemakkelijk in dat de som van de cijfers van $7111\!\dots\!111$ een drievoud is, en zodoende is dit getal ook deelbaar door $3$, en dus zeker niet priem. Het volstaat nu de gevallen te analyseren waarin $n$ deelbaar is door $3$. Merk daartoe op dat zes cijfers aan het getal toevoegen gedaan kan worden middels $106 \cdot 7111\!\dots\!111 + 111111$. Omdat $111111 = 1001\cdot 111 = (7\cdot 11\cdot 13)\cdot(3\cdot 37)$, vinden we dat, indien een getal van de vorm $7111\!\dots\!111$ deelbaar is door $7$ of $13$, het getal met zes extra enen dat ook zijn. Nu blijkt het zo te zijn dat inderdaad $7111 = 13 \cdot 547$ deelbaar is door $13$ en $7111111 = 7000000 + 111111$ is duidelijk deelbaar door $7$. Dit bewijst dat als $n$ deelbaar is door $3$, het getal $7111\!\dots\!111$ dan ofwel deelbaar is door $7$, ofwel door $13$, en dus kan het niet priem zijn.
Opgave 532 [ooO]
We beweren dat het minimale aantal stappen dat de loper moet doen gelijk is aan 36. Het is gemakkelijk om hiervan een voorbeeld te vinden; zie de afbeelding.
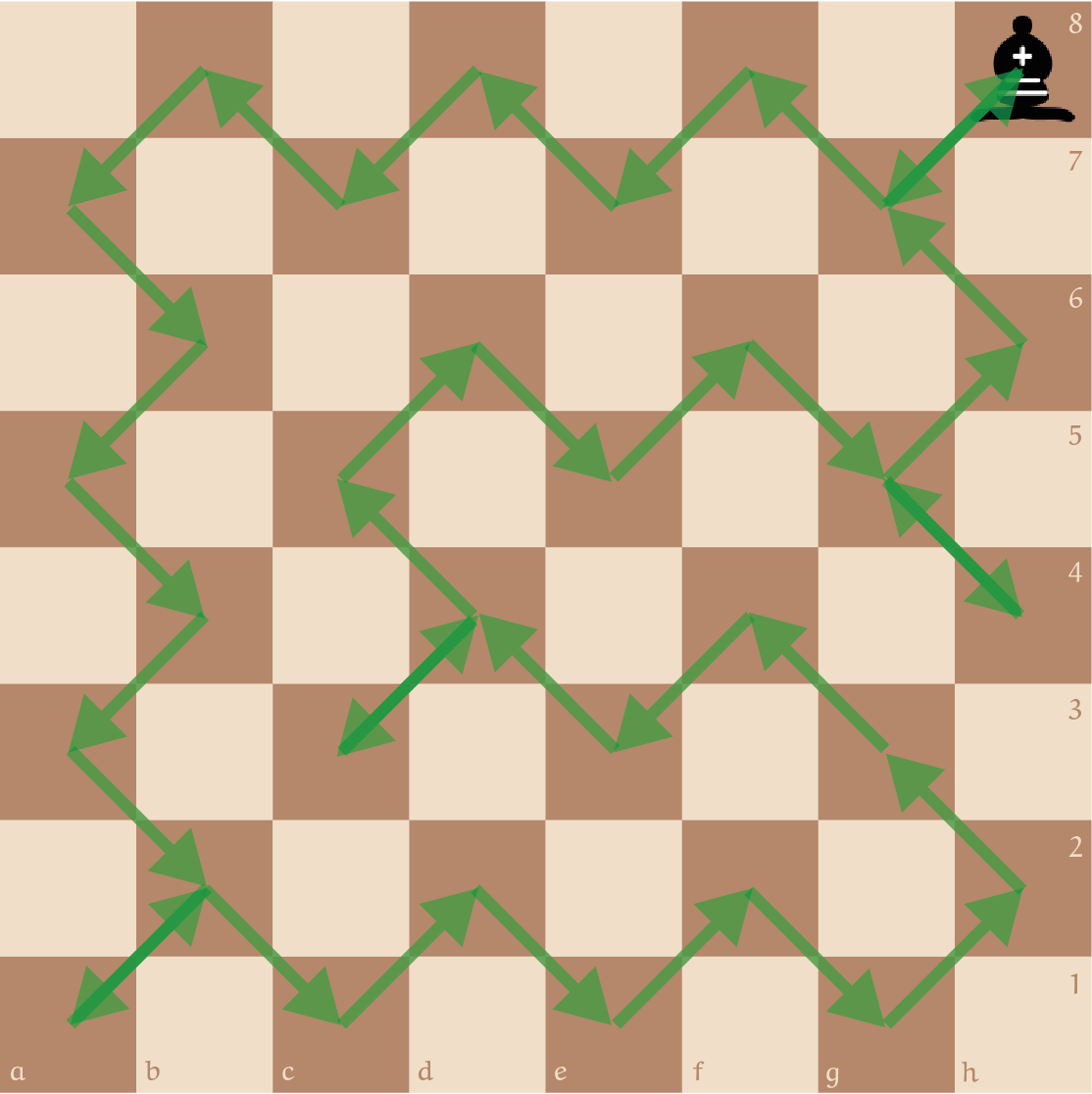
Het is ook gemakkelijk om in te zien dat het niet kan in 32 stappen, omdat de zwarte hoekvakjes enkel vanuit één vakje bereikt kunnen worden, dus daar moet de loper zeker heen en weer lopen. Ten slotte merken we op dat de lengte van het pad van de loper altijd even lengte heeft; namelijk, de loper stapt afwisselend van vakjes met een cirkel naar vakjes zonder en weer terug.

Het resteert dus om aan te tonen dat een circuit van 34 stappen niet mogelijk is. We veronderstellen nu voor een tegenspraak dat het wel kan in 34 stappen. Dan bezoekt de loper dus elk vakje precies één keer, behalve de twee vakjes die grenzen aan de zwarte hoekvakjes, omdat hij die sowieso twee keer moet bezoeken. Als een zwart vakje dan bereikt kan worden vanuit precies twee andere vakjes, dan moet de loper wel komen vanaf het ene vakje, en gaan naar het andere vakje; teruglopen is namelijk niet toegestaan. Dit toont aan dat de loper een stap moet zetten over alle zwarte lijnstukjes in de figuur.

Dit is echter onmogelijk, daar de loper dan al een gesloten circuit heeft afgelegd, en zodoende er niet in is geslaagd om de vakjes in het midden van het bord te bereiken. Hiermee is het bewijs voltooid.
