Opgave 1

Eerst nemen we aan dat $ab \neq 0$. Dan heeft de lijn $l$ de vergelijking $y=\frac{-a}{b}x - \frac{c}{b}$ en heeft de lijn door $P$ loodrecht op $l$ de vergelijking $y = \frac{b}{a}x+\frac{aq-bp}{a}.$ Simultaan oplossen geeft $x=\frac{b^2p-abq-ac}{a^2+b^2}$ en $y=\frac{a^2q-abp-bc}{a^2+b^2}.$ Dan is de afstand van $P$ naar $l$ gelijk aan $\sqrt{\left(p-\frac{b^2p-abq-ac }{a^2+b^2}\right)^2+ \left(q-\frac{a^2q-abp-bc}{ a^2+b^2}\right)^2.}$

Breng alles onder één noemer en ontbind in factoren; dit wordt $\sqrt{\frac{(a^2+b^2)(ap+bq+c)^2}{(a^2+b^2)^2}} = \frac{|ap+bq+c|}{\sqrt{a^2+b^2}}.$  Hierbij wordt gebruik gemaakt van het feit dat $\sqrt{m^2} = |m|.$

Je kunt checken dat de formule het gewenste antwoord geeft als $a = 0$ of $b = 0$. Bijvoorbeeld: als je $a = 0$ invult in de formule krijg je $|q + c/b|,$ precies gelijk aan de afstand van horizontale lijn $y = -c/b$ tot punt $P$ met y-coördinaat $q.$

Opgave 2

Voor dit bewijs nemen we eerst aan dat $b \neq 0$. Dan heeft de lijn $l$ de vergelijking $y=\frac{-a}{b}x-\frac{c}{b}$ en heeft de cirkel de vergelijking $(x-p)^2 + (y-q)^2 = r^2$. Als we deze twee vergelijkingen combineren om één vergelijking in $x$ te krijgen komen we uit op

$$(x-p)^2 + \left(\frac{ax+c}{b}+q\right)^2 =r^2$$.

Als we dit meer expliciet als een kwadratische vergelijking schrijven wordt het: $$\frac{a^2+b^2}{b^2}x^2 + 2\left(\frac{ac}{b^2} + \frac{aq}{b} –p\right)x + \left(p^2+q^2+\frac{2cq}{b}+\frac{c^2}{b^2}-r^2\right)=0.$$

Stel de discriminant gelijk aan 0 en we krijgen de vergelijking voor de waarde van $r$ die gelijk is aan de afstand van punt $P$ naar lijn $l$.

$$4\left(\frac{ac}{b^2} + \frac{aq}{b} - p\right)^2 - 4\frac{a^2+b^2}{b^2}\left(p^2 + q^2 + \frac{2cq}{b} + \frac{c^2}{b^2}-r^2\right)=0.$$

Met goed boekhouden levert dit 16 termen waarvan 8 verdwijnen en wonder boven wonder blijft over: $r^2 =\frac{(ap+bq+c)^2}{a^2+b^2}$ en $r=\frac{|ap+bq+c|}{\sqrt{a^2+b^2}}.$

Opgave 3

Bij het zoeken naar een algemene formule biedt een vectormethode uitkomst. Hier hoeven we geen aannames te maken over de waarden van $a$ of $b$. De vector $\vartheta$ is gelijk aan $\frac{1}{\sqrt{a^2+b^2}}\left(\begin{matrix}a\\b\end{matrix}\right).$ De vector $\left(\begin{matrix}p\\q\end{matrix}\right) + \mu\cdot\frac{1}{\sqrt{a^2+b^2}}\left(\begin{matrix}a\\b\end{matrix}\right)$ eindigt op lijn $l$ voor de juiste keuze van $\mu.$ Dit geeft:

$a\cdot\left(p+\frac{\mu\cdot a}{\sqrt{a^2+b^2}}\right)+b\cdot\left(q+\frac{\mu\cdot b}{\sqrt{a^2+b^2}}\right)+c = 0$ en de oplossing wordt $|\mu|=\frac{|ap+bq+c|}{\sqrt{a^2+b^2}}.$ Dit bewijs gaat heel snel en heeft de volgende voordelen:

• De absolute waarde heeft betekenis, want we weten niet of $\vartheta$ wijst in de richting van $P$ naar $l$ of van $l$ naar $P$.
• De wortel is begrijpelijk want het ontstaat in het proces van het maken van eenheidsvector $\vartheta$.
• Het is voor alle lijnen en punten te gebruiken.
• Het berekent de afstand van $P$ naar $l$ direct zonder tussenstappen.
• Het verklaart waarom $p$ en $q$ in de plaats van $x$ en $y$ komen in de lijnformule.

Opgave 4

De raaklijn heeft richtingscoëfficiënt $\frac{(p-a)}{(b-q)}$ omdat hij loodrecht staat op de straal die eindigt in punt $(a, b).$ Omdat de raaklijn door het punt $(a, b)$ gaat, is de formule: $y=\frac{(p-a)}{(b-q)}x+c,$ waar $c$ gevonden kan worden door $a$ en $b$ in te vullen voor $x$ en $y$. Dit geeft de formule $y=\frac{(p-a)}{(b-q)}x+\frac{b(b-q)-a(p-a)}{(b-q)}$ voor alle niet-verticale raaklijnen. Vermenigvuldigen met de noemers geeft $y(b-q) = x(p-a) + b(b-q) - a(p-a),$ waaruit volgt $(y-b)(b-q) = (x-a)(p-a)$. De vorm met $r$ is te krijgen door de laatste formule te herschrijven als $(y-q + q-b)(b-q) = (x-p + p-a)(p-a).$ Dit geeft $(y-q)(b-q) + (q-b)(b-q) = (x-p)(p-a) + (p-a)(p-a)$ en uiteindelijk $(x-p)(a-p) + (y-q)(b-q) = (p-a)^2 + (q-b)^2 = r^2$ en die geldt voor alle lijnen.

Opgave 5

Het punt $(a, b)$ ligt op de cirkel met middelpunt $(p, q)$ en straal $r + d,$ met $d$ de afstand van $(a, b)$ tot de cirkel met straal $r.$ Dan geldt: $(a- p)^2 + (b- q)^2 = (r + d)^2.$ Dan hebben we voor $d: d = |\sqrt{(a-p)^2+(b-q)^2}-r|.$

Opgave 6

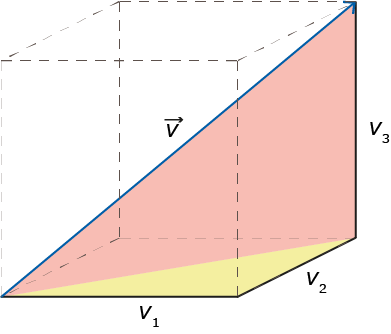
Een driedimensionale vector $\vec{v} = \left(\begin{matrix}v_1\\v_2\\v_3\end{matrix}\right)$ heeft drie componenten. De lengte van vector $\vec{v}$ is $\sqrt{v_1^2+v_2^2+v_3^2}.$ Dit is te bewijzen door de stelling van Pythagoras twee keer te gebruiken in de gekleurde driehoeken van figuur 1.

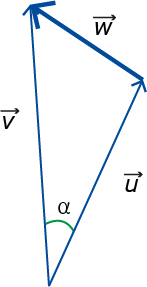
In figuur 2 zijn twee driedimensionale vectoren $\vec{u}$ en $\vec{v}$, de hoek $\alpha$ tussen de twee vectoren en een derde vector $\vec{w}=\vec{v}-\vec{u}.$ Door de cosinusregel hier toe te passen krijgen we twee uitdrukkingen voor de scalaire product van de twee vectoren.

$$\vec{v}\cdot \vec{u}=v_1u_1+v_2u_2+v_3u_3=|\vec{v}|\cdot|\vec{u}|\cdot \cos(\alpha).$$

De absolute waarde tekens zijn hier symbolen voor de lengtes van de twee vectoren. Nu kunnen we vector $\vec{u}$ door een vector in dezelfde richting met lengte 1 vervangen. Dan is het scalaire product van de twee vectoren gelijk aan $|\vec{v}|\cdot \cos(\alpha)$ en dit is de zijde die we zoeken. Zelfs als hoek $\alpha$ groter is dan 90° ontstaat er geen probleem met een negatieve uitkomst aangezien van deze waarde uiteindelijk het kwadraat wordt genomen.

De twee formules voor afstanden in drie dimensies zijn:

• Afstand van punt $(p, q, r)$ tot het vlak $ax + by - cz + d = 0:$
  $$\frac{|ap+bq+cq+d|}{\sqrt{a^2+b^2+c^2}}.$$

• Afstand van punt $(p, q, r)$ tot de lijn $\left(\begin{matrix}x\\y\\z\end{matrix}\right)= \left(\begin{matrix}a\\b\\c\end{matrix}\right)+\lambda \left(\begin{matrix}u\\v\\w\end{matrix}\right)$ is
  $$\sqrt{(p-a)^2+(q-b)^2+(r-c)^2-\left[\left(\begin{matrix}p-a\\q-b\\r-c\end{matrix}\right)\cdot \frac{1}{\sqrt{u^2+v^2+w^2}}\left(\begin{matrix}u\\v\\w\end{matrix}\right)\right]^2}$$