Alle berekeningen in het septembernummer waren toegepast op één specifiek voorbeeld. Zij lieten zien hoeveel verschillende methodes leiden naar hetzelfde resultaat, maar om te kunnen spreken van een echte stelling hebben we een algemene formule nodig. In principe zouden we elke methode kunnen nemen als het beginpunt in een poging om een algemene formule af te leiden, maar eerst moeten we een algemene formule voor lijn $l$ hebben die ook geldig is voor verticale lijnen. Dit wordt $ax + by + c = 0.$ De coördinaten van $P$ noemen we $(p, q).$

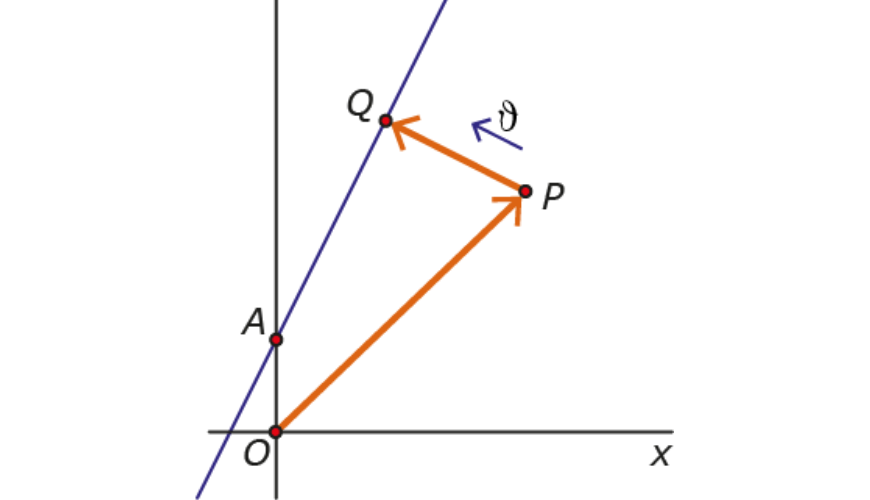
De eerste afleiding gaat uit van een lijn door $P$ die loodrecht staat op lijn $l$ zoals in figuur 1. Begin met de aanname dat $l$ niet een verticale of horizontale lijn is. Dan zijn $a$ en $b$ allebei niet gelijk aan nul. Als we voor dit soort lijnen een formule hebben, kunnen we later checken of de formule ook werkt voor horizontale en verticale lijnen.

Opgave 1

Vind deze afleiding en check dat het in alle gevallen werkt.

Als tussenstap in deze afleiding wordt de $x$-coördinaat van het snijpunt van de twee lijnen gevonden. Een hoop andere methodes vinden ook deze $x$-waarde en zijn daarna identiek aan deze afleiding.

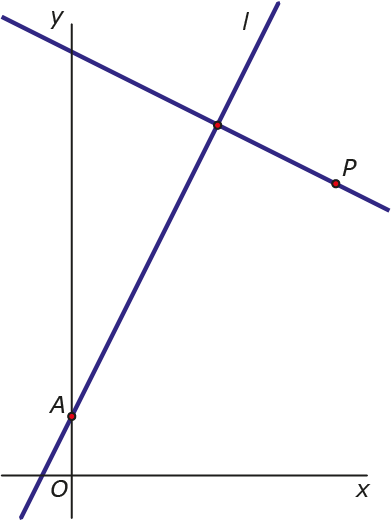
Een tweede afleiding vindt de afstand van punt $P$ en lijn $l$ direct.

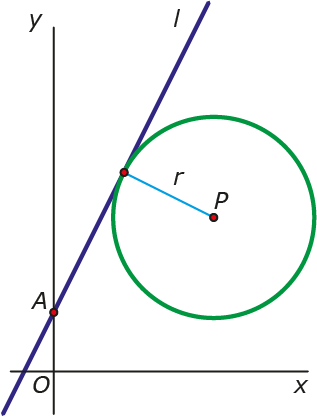
In deze afleiding maken we gebruik van een cirkel met middelpunt $P$ zoals te zien is in figuur 2. Om de straal $r$ van deze cirkel gelijk te maken aan de afstand van punt $P$ naar lijn $l$ moet een discriminant gelijk zijn aan nul.

Opgave 2

Vind zo’n afleiding en check dat je precies dezelfde formule hebt als in opgave 1.

Deze eerste twee afleidingen zijn vrij lastig. Ze zijn allebei algebraïsch ingewikkeld. Een derde bewijs laat zien dat het veel makkelijker en overzichtelijker kan. Dit is een vectormethode, waarbij eerst een vector begint in de oorsprong $O$ en eindigt in punt $P.$ Vervolgens start een tweede vector in $P$ die eindigt in $Q$ en loodrecht staat op $l.$ Deze vector is een veelvoud van een eenheidsvector $\vartheta$. Deze situatie is in figuur 3 te zien.

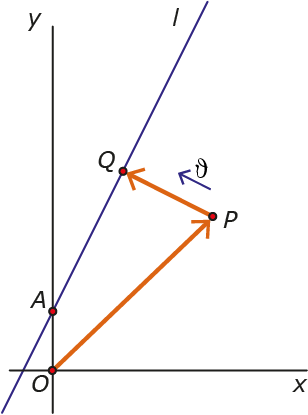
Opgave 3

Vind deze afleiding en check dat je weer precies dezelfde formule hebt als in opgave 1 en 2.

Uitbreidingen

De formule voor de afstand tussen een punt en een lijn lijkt een soort kruising te zijn tussen de formule voor lijn $l$ en de coördinaten van punt $P.$ Ik ging op zoek naar andere voorbeelden van dergelijke formules en heb er twee gevonden.

De eerste is de formule voor de raaklijn aan een cirkel met middelpunt $(p, q),$ straal $r$ en raakpunt $(a, b)$  zoals te zien is in figuur 4.

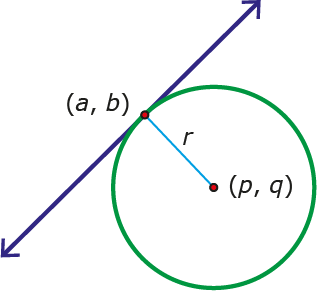
De formule is $(a - p) \cdot (x - p) + (b - q) \cdot (y - q) = r^2.$

Dit lijkt op de formule van de cirkel zelf met de coördinaten van het raakpunt ingevuld.

Opgave 4

Laat zien dat dit een lijnformule is van een lijn die door het raakpunt gaat en de juiste richtingscoëfficiënt heeft. Je kunt ook de formule zelf afleiden.

Het tweede voorbeeld is de formule voor de kortste afstand van een punt tot een cirkel.

Opgave 5

Vind deze formule.

In drie dimensies

Er zijn nog twee uitbreidingen naar drie dimensies die analoog lopen met de vectormethodes in het vlak. Hier is de aanvulling op de Stelling van Pythagoras voor de afstand tussen twee punten in de ruimte nodig en ook de toevoeging van het inproduct van twee vectoren in drie dimensies.

De eerste uitbreiding is de formule voor de afstand van een punt $(p, q, r)$ tot een vlak, $ax + by + cz + d = 0.$ Het bewijs gaat net als bij de methode in opgave 3.

De tweede uitbreiding is de formule voor de afstand van een punt (p, q, r) tot een lijn

$$\left(\begin{matrix}x\\y\\z\end{matrix}\right) = \left(\begin{matrix}a\\b\\c\end{matrix}\right) + \lambda \left(\begin{matrix}u\\v\\w\end{matrix}\right).$$

De afleiding maakt gebruik van het inproduct van twee vectoren in drie dimensies.

Opgave 6

Vind deze twee formules.

 

Bekijk oplossing