Nadat de inhoud van een verpakking wordt bepaald, is er nog de keuze voor de vorm van de verpakking. Laten we een blik bekijken: hoe groot wordt de straal van de cirkel aan de boven- en onderkanten en wat moet dan de hoogte van het blik zijn? Er zijn veel mogelijke criteria voor het beste blik: financiële, esthetische en praktische. De hoeveelheid metaal die nodig is om het blik te maken is een financiële factor en met wiskunde kunnen we bepalen wat in dat opzicht de beste vorm is. De keuze valt dan op het blik met de juiste inhoud en de kleinste oppervlakte. Dit optimaliseringsprobleem maakt gebruik van differentiaalrekening om de minimale oppervlakte aan gebruikt metaal te bepalen.

De oplossing vind je als volgt:

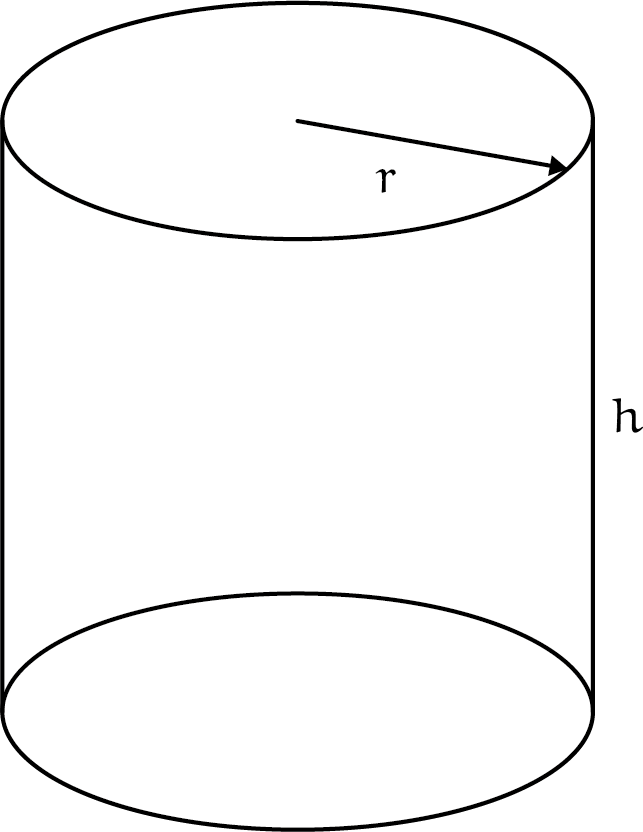
1. Maak een formule voor de inhoud van de cilinder in termen van $r$ (de straal van het grondvlak) en $h$ (de hoogte van de blik). Zie figuur 1.
2. Kies de vaste inhoud van het blik en schrijf een formule voor $h$ in termen van $r$ en de inhoud (bijvoorbeeld $400\ ml$).
3. Maak de formule voor de oppervlakte van de cilinder in termen van $r$ en $h$ en gebruik de formule van stap 2 waarin h is uitgedrukt in $r$ (substitutie).
4. Nu heb je een formule voor de oppervlakte in termen van $r$ alleen. Neem de afgeleide van deze formule en stel de afgeleide gelijk aan $0$ om de waarde van $r$ te bepalen die een minimale oppervlakte oplevert en controleer dat het inderdaad een minimum is.
5. Kijk terug naar stap 2 en bepaal de bijbehorende waarde van $h$.
6. Hoewel deze waarden van $r$ en $h$ wat ingewikkeld zijn is hun verhouding heel simpel.

 

Opgave 1 Bepaal de verhouding van $r$ en $h$ voor dit beste blik door de 6 stappen te doorlopen.

 

Opgave 2 Stel dat je een blik met een inhoud van $400\ ml$ wilt maken maar nu met een open bovenkant. Wat is dan de verhouding van $r$ en $h$ bij een minimale oppervlakte?

 

Opgave 3 Stel dat je een cupcake wilt maken met een geplooid stuk papier zoals in figuur 2. Dit papiertje is cirkelvormig, waarbij de rand wordt gevouwen zodat dit de zijkant van de cupcake vormt. We gaan voor het gemak uit van een cilindervormige cupcake, dus plat aan de boven- en onderkant. De inhoud van deze cupcake is $100\ ml$. Welke verhouding tussen de straal van de cirkel aan de onderkant en de hoogte van de geplooide verticale zijwand hoort bij het minimale gebruik van papier?

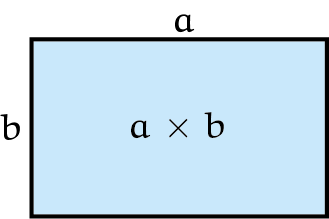
Tot nu toe maken alle exemplaren gebruik van cirkels, maar cirkels naast elkaar uit snijden, geeft veel snijafval. Een doos met overal rechthoeken als zijvlakken heeft dat probleem niet. Noem de zijden van de rechthoek aan de bovenkant $a$ en $b$ en de hoogte van de doos $c$. De inhoud van de doos is dan gelijk aan $a \times b \times c$. Wat zou de beste keuze voor $a$, $b$ en $c$ zijn voor de gekozen inhoud? Om dit te bepalen, maken we eerst een tussenstap en kijken naar één zijvlak van de doos. We gaan de meest efficiënte vorm bepalen (met de kleinste omtrek) gegeven de oppervlakte.

Opgave 4 Gebruik de 6 stappen om te bewijzen dat voor alle rechthoeken met een vaste oppervlakte $A$ het vierkant de kleinste omtrek heeft.

Nu terug naar de doos met dimensies $a \times b \times c$. Stel dat de bovenkant van de doos de dimensies $a$ en $b$ heeft. Dan is een kleinere oppervlakte te bereiken door dat rechthoek te vervangen door een vierkant met zijden gelijk aan $y=\sqrt{ab}$. Nu kan je de 6 stappen doen met de variabelen $y$ en $c$.

Opgave 5 Laat zien dat van alle dozen met een vaste inhoud de kubus het minimale oppervlakte heeft.

 

Opgave 6 In figuur 4 zie je alle $11$ mogelijke uitslagen voor een kubus. Welke zou jij kiezen als sjabloon bij het produceren van kubussen?

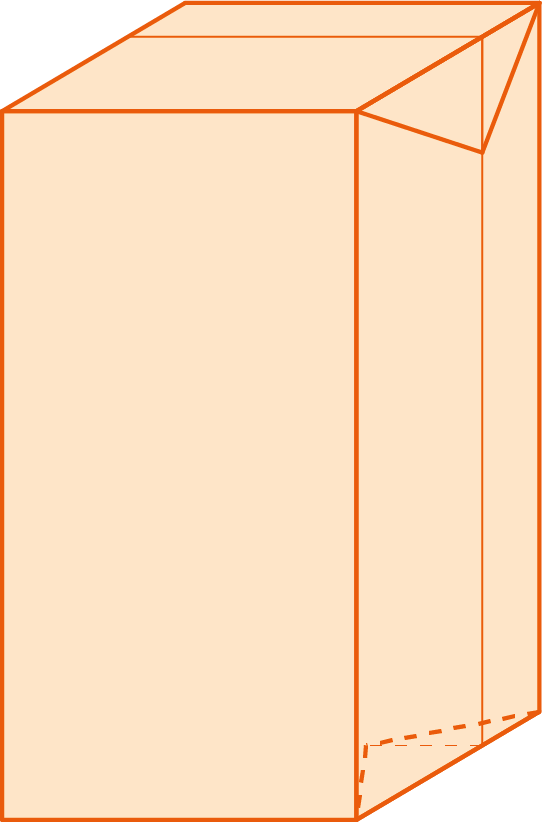
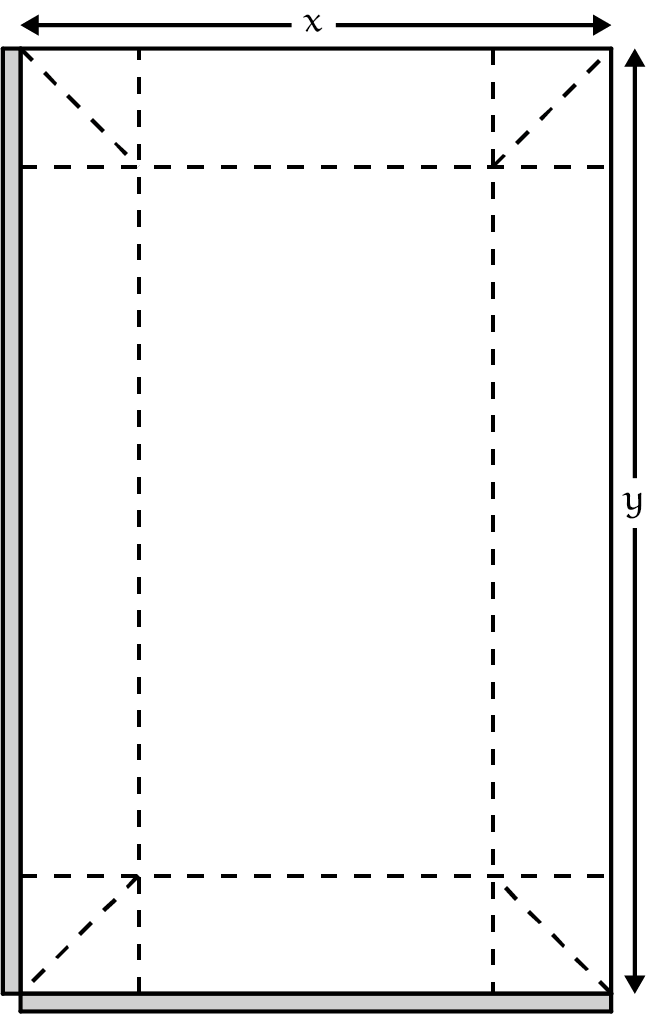
Van metaal en papier gaan we nu naar karton en ik hou vast aan een vierkante bovenkant. Kijk naar figuur 5 waar een pak wordt gemaakt van een stuk karton met de afmetingen $2x$ en $y$. In figuur 5b is het pak dubbel gevouwen: de voorkant is te zien met een open bovenkant, afgesloten linker- en onderkant en omgevouwen en doorlopende rechterkant. De stippellijnen zijn vouwlijnen en die zijn ook op de achterzijde. Bij het vouwen van dit pak komen er oortjes aan de onder- en bovenkant en deze vouwen we naar binnen aan de onderkant (zie gestippeld in figuur 5a) en naar buiten langs de zijkanten aan de bovenkant.

Opgave 7 Stel de gewenste inhoud op $1000\ ml$. Bepaal de verhouding van $x$ en $y$ bij het pak met minimale oppervlakte. Wat is dan de verhouding tussen de zijde van de vierkante top en de lengte van het pak in de $y$-richting?

Deze pakken worden altijd iets groter gemaakt om wat marge te hebben bij het openmaken. Dit verandert de waarden van $x$ en $y$ maar niet hun verhouding. Er zijn twee manieren om marge in te bouwen.

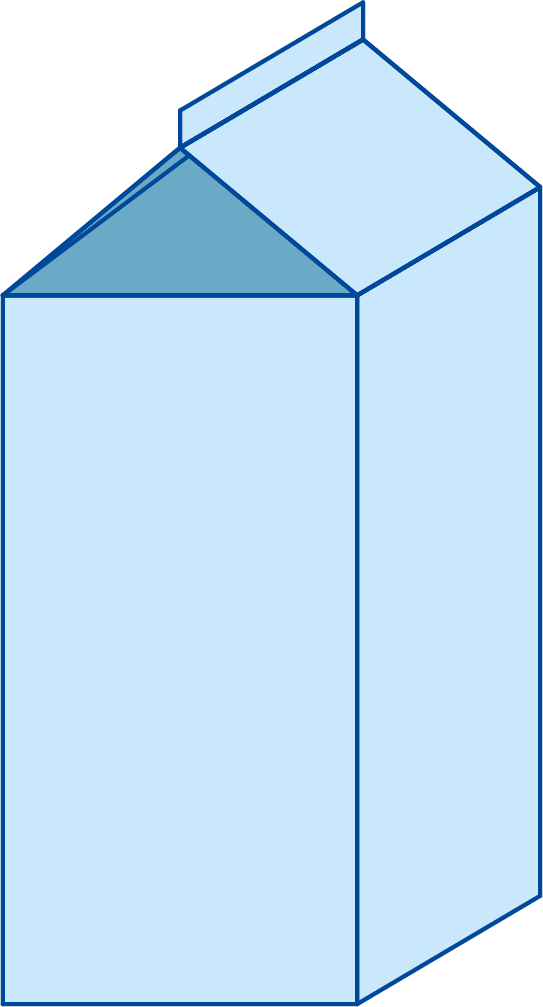
De eerste optie is gewoon het pak te verhogen met een lengte $d$. Als de zijden van de vierkante bovenkant een lengte $s$ hebben dan vormt dit een balkvormige $s \times s \times d$ ruimte.

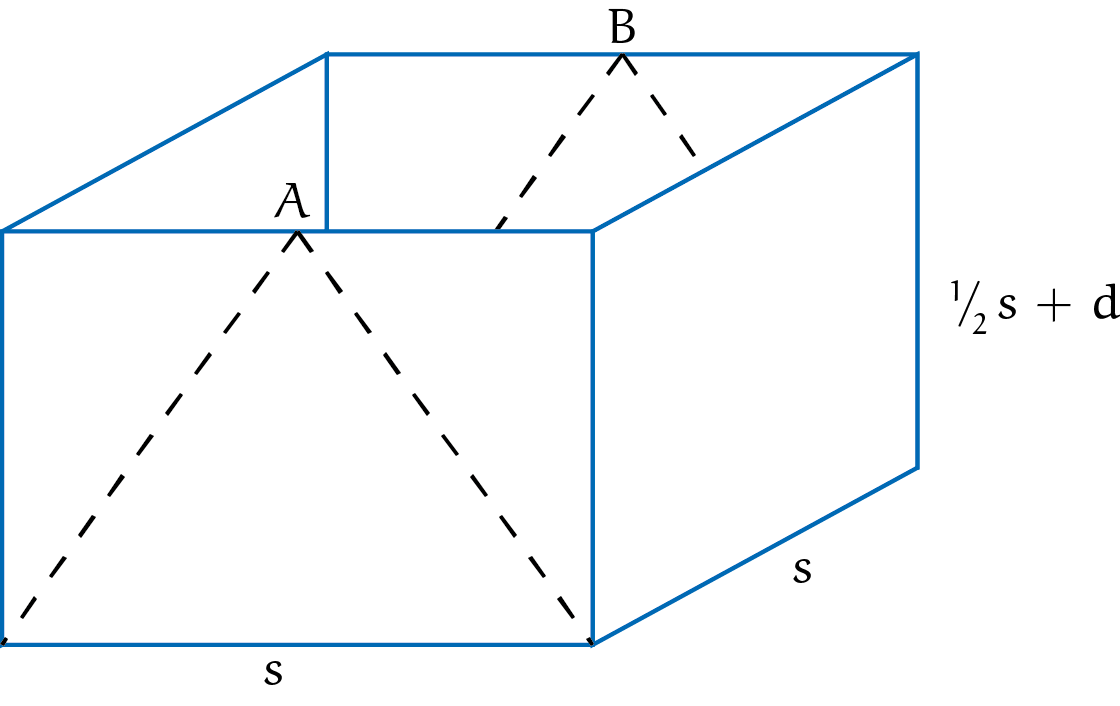
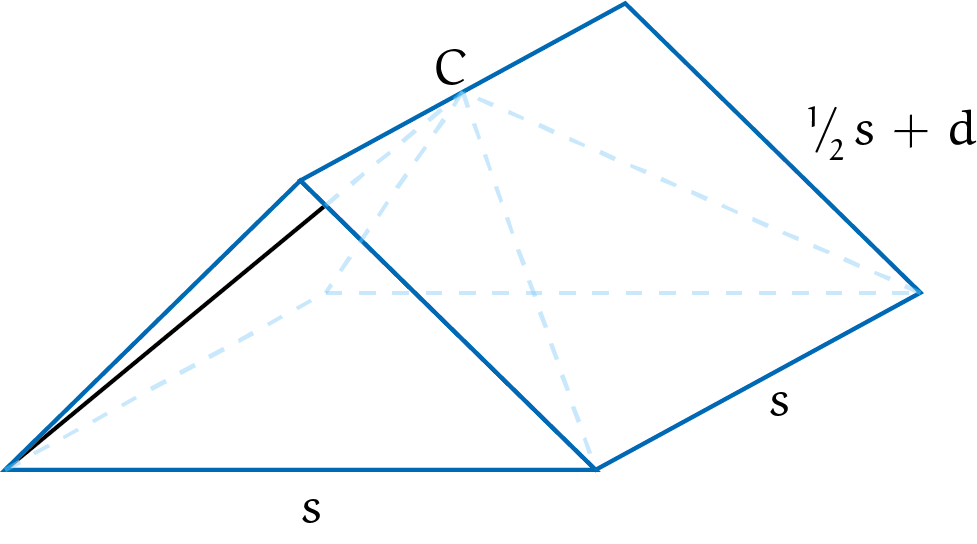
Voor de tweede optie zie figuur 6. Daar wordt marge ingebouwd door een soort dakje te vouwen aan de bovenkant. Bij het vouwen komen de punten $A$ en $B$ samen in punt $C$, de twee dakhelften hebben een afmeting van $s \times (\frac{s}{2} + d)$ en de voor- en achterkant worden zo gevouwen dat een piramidevormige binnenruimte ontstaat. Met deze tweede optie kan ook een zijkant worden uitgevouwen om een handig tuitje van te maken.

Opgave 8 Voor welke waarden van $d$ geeft de tweede optie meer ruimte dan de eerste optie?

 

Bekijk oplossing