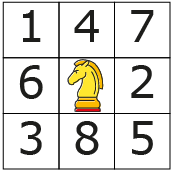
Enige tijd geleden bekeek ik een paardensprong in een 'woordkraker' van de Volkskrant. Je kent die paardensprong waarschijnlijk wel. Door middel van een paardensprong uit het schaakspel (één vakje opzij en tegelijkertijd twee omhoog of varianten daarop: twee naar links en één naar beneden, enzovoorts), moet een woord van acht letters worden achterhaald. Die paardensprong was zoals in figuur 1 aangegeven.

Het probleem bij de paardensprong is natuurlijk: waar begin je? In eerste instantie las ik, beginnend bij de 'r' linksboven: 'rechter', maar de achtste letter was dan een 'f', dus dat was het gevraagde woord rechterf geweest; niet echt een Van Dale-woord…. (Of de 'f' had een 't' moeten zijn, dan was trechter mogelijk geweest, bij die 't' beginnend. Maar goed, die extra 't' in plaats van de 'f' stond er niet…).

Opgave 1 Wat is het gezochte woord bij deze paardensprong?

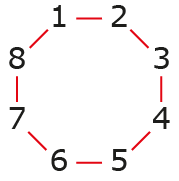
Als je goed over deze paardensprong nadenkt, zijn er maar een beperkt aantal mogelijke woorden van acht letters te maken. Geven we de acht vakjes nummers, dan is bijvoorbeeld, linksboven beginnend met een 1 en na het kiezen van vakje 2, er maar één voortzetting mogelijk. Let op: je kunt, afhankelijk van je start positie, niet alleen rechtsom ('met wijzers van de klok mee'), maar ook linksom, zie figuur 2.

 

Opgave 2 Hoeveel combinaties van acht cijfers (en dus letters) zijn er mogelijk bij de paardensprong?

Zonder het antwoord direct te prijs te geven, laat figuur 3 zien wat het aantal mogelijkheden van opgave 2 is. Een (8-)paardensprong is op te vatten als een cirkel van acht mogelijkheden die in twee richtingen te lezen is.

We gaan terug naar de paardensprong van opgave 1. Zou het kunnen dat er twee Nederlandse woorden mogelijk zijn bij deze puzzelsoort? Uiteraard zal een puzzelmaker daar naar kijken, want meestal wordt er maar één antwoord gewenst. Met een tweede mogelijk woord bedoel ik niet flauwe koppels als boomstam-stamboom of meststalstalmest. Dat zijn gewoon lettergreepverwisselingen. En ook niet het al iets leukere stel intussen-tussenin. Nee, ik bedoel een 'tegendraads' stel. Zijn er misschien woordkoppels mogelijk bij een paardensprongpuzzel, waarbij een van de twee woorden 'de andere kant op' gelezen kan worden? Ja, maar niet veel. Het enige Nederlandse 'tegendraadse' koppel dat ik ken staat in figuur 4. Ik heb hierin alleen één letter vervangen door een vraagteken.

Opgave 3 Welke twee woorden kunnen met paardensprongen worden gemaakt? (En wat is dus de ontbrekende letter?)

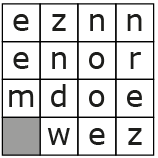
In Rutger Kiezebrink's rubriek 'Taalpuzzels' in Onze Taal stond in het mei/juni-nummer van 2023 ook een paardensprong, maar dan in een afwijkende vorm: een (bijna) 4-bij-4 vierkant. Eén van de zestien velden deed niet mee, zodat er een '15-paardensprong' ontstond, zie figuur 5.

De letterlijke tekst van Kiezebrink bij de opgave was: 'Spring met de paardensprong (zoals bij schaken) een vijftienletterwoord bij elkaar dat bij juni hoort. Elke letter wordt één keer gebruikt. Begin in een van de hoeken.' Het is niet gemakkelijk met paardensprongen alle velden van vierkante of rechthoekige borden precies één keer te bezoeken. Bij een 4-bij-4-vierkant lukt het in ieder geval niet. De beroemde Engelse puzzelmaker Henry Dudeney liet ruim een eeuw geleden zien dat het wel op een 5-bij-4-bord kan.

Opgave 4 Laat zien dat er een route op een 5-bij-4-bord bestaat. Opgave 5 Wat is het gevraagde woord van de 15-paardensprong? (Hint: denk aan de maand waarin deze puzzel verscheen.)

Er werd in die 15-paardensprong ook indirect gevraagd naar het aantal verschillende routes dat mogelijk is, zoals we dat ook deden bij de '8-paardensprong'. Het hoekvakje rechtsboven (met de 'n') kan daarbij geen startpunt zijn. Dit is met een prachtige en eenvoudige manier aan te tonen. Kleur alle velden als een bij een schaak- of dambord zwart en wit.

Opgave 6 Bewijs met de bovengenoemde kleuring dat het hoekvakje rechtsboven geen startpunt van een 15-route kan zijn. Opgave 7 Hoeveel routes zijn er te maken in de 15-paardensprong, uitgaande van alleen de overgebleven twee hoekpunten als startpunt?

 

		Meer weten? Een aantal van deze opdrachten zullen als puzzels worden gepubliceerd in Denkstof, New Scientist, najaar 2024.