Als we ons beperken tot reeksen van drie blijken er drie verschillende categorieën te zijn:

1. $\rm KKK$ en $\rm MMM$ Hiervoor zijn gemiddeld 14 worpen nodig
2. $\rm KMK$ en $\rm MKM$ met gemiddeld 10 worpen
3. $\rm KMM$, $\rm MMK$, $\rm MKK$ en $\rm KKM$ die gemiddeld in 8 worpen worden bereikt.

Stel een casino introduceert een kop of munt spel met de volgende regels

1. De speler kiest van tevoren een patroon met lengte 3 (bijv. $\rm KMK$)
2. Er kan geworpen worden met één munt voor 1 euro per worp
3. Wanneer het gekozen patroon ‘verschijnt’ - dus in ons voorbeeld in drie achtereenvolgende worpen Kop, Munt en vervolgens weer Kop - wordt er 10 euro uitgekeerd.

Het spelen is dan alleen gunstig wanneer je kiest voor een patroon uit groep C.

Een casino zal het spel in deze vorm niet aanbieden omdat het voor hen natuurlijk niet lucratief is, dus we kijken naar een andere optie.

Twee spelers kiezen ieder een patroon (bijv. de een $\rm KMK$ en de ander $\rm KMM$) en gooien om beurten ieder met hun eigen munt net zo lang tot een van de twee door hem/haar voorspelde patroon heeft gegooid.

Het ligt voor de hand dat een keuze uit groep C slimmer is dan een keuze uit groep A of B. Maar een de verwachtingswaarde zegt nog niet alles!

Een simpel voorbeeld ter illustratie. Denk aan twee goedkope speeltjes:

speeltje $X$ gaat na $6$, $7$ of $8$ keer gebruiken kapot (met gelijke kansen);

speeltje $Y$ gaat na $1$, $9$ of $10$ keer kapot (ook met gelijke kansen).

De verwachte levensduur van speeltje $X$ is $7$ (keer), van $Y$ net iets minder $(20/3)$. Toch zal bij vergelijking $Y$ twee van de drie keer winnen. Alleen wanneer speeltje $Y$ de eerste keer kapot gaat wordt verloren van $X$, anders functioneert het net iets langer dan $X$. Niet alleen het gemiddelde is van belang, het gaat om de hele kansverdeling.

De kansverdeling van het aantal benodigde worpen voor een bepaald patroon is nog niet zo eenvoudig te bepalen. Het begin is goed te doen. We kijken eerst naar het aantal worpen $A$ dat nodig is om de reeks $\rm KMK$ te krijgen.

$P(A = 3) = P({\rm KMK}) = 1/8$

$P(A = 4) = P( . {\rm KMK}) = 1/8$. De eerste worp is niet van belang

$P(A = 5) = P(\not{\rm \!\!K}\!\not{\rm \!\!M}{\rm KMK})= 3/4 \times 1/8= 3/32$. De eerste twee worpen mogen niet $\rm KM$ zijn, want dan is het na $3$ worpen al afgelopen.

$P(A = 6) = P({\rm ???KMK})$. Voor $???$ mag niet worden ingevuld: $\rm KMK$, $\rm KKM$ of $\rm MKM$ Dus $P(A = 6) = 5/8 \times 1/8 = 5/64$.

Hierna wordt het steeds lastiger.

Een manier om de grip te krijgen op de kansverdeling is gebruik te maken van een matrix van overgangskansen bij de Markov-ketens (zo heten de schema’s die we in de vorige aflevering ook al gebruikten). Voor $\rm KMK$ ziet de Markov-keten er als volg uit:

De bijbehorende kansenmatrix is:

0,5		0,5
0,5	0,5
	0,5
		0,5

In de derde kolom kun je aflezen dat de kans om van tussenstand 3 ($\rm KM$) naar eindstand 4 ($\rm KMK$) te gaan 0,5 is evenals de kans om van tussenstand 3 terug te gaan naar de beginstand. De lege plekken geven aan dat de waarde daar $0$ is. Met matrices (meervoud van matrix) kun je, met geschikte software of op je grafische rekenmachine, goed rekenen. Voor ons doel zijn vooral de machten van belang. Zo ziet de achtste macht van bovenstaande matrix er als volgt uit:

0,1445	0,1094	0,0820	0,0000
0,1914	0,1445	0,1094	0,0000
0,1094	0,0820	0,0625	0,0000
0,0625	0,0469	0,0352	0,0000

Eigenlijk is alleen het getal linksonder van belang (0,0625) Hier lezen we af dat de kans dat de gewenste eindstand ($\rm KMK$) na precies acht worpen wordt bereikt gelijk is aan 0,625 $(1/16)$.Op deze manier kunnen we voor alle mogelijke patronen de kansverdeling bepalen. Hieronder een grafische voorstelling van (een deel van) de kansverdeling voor $\rm KKK$, $\rm KMK$, en $\rm KKM$:

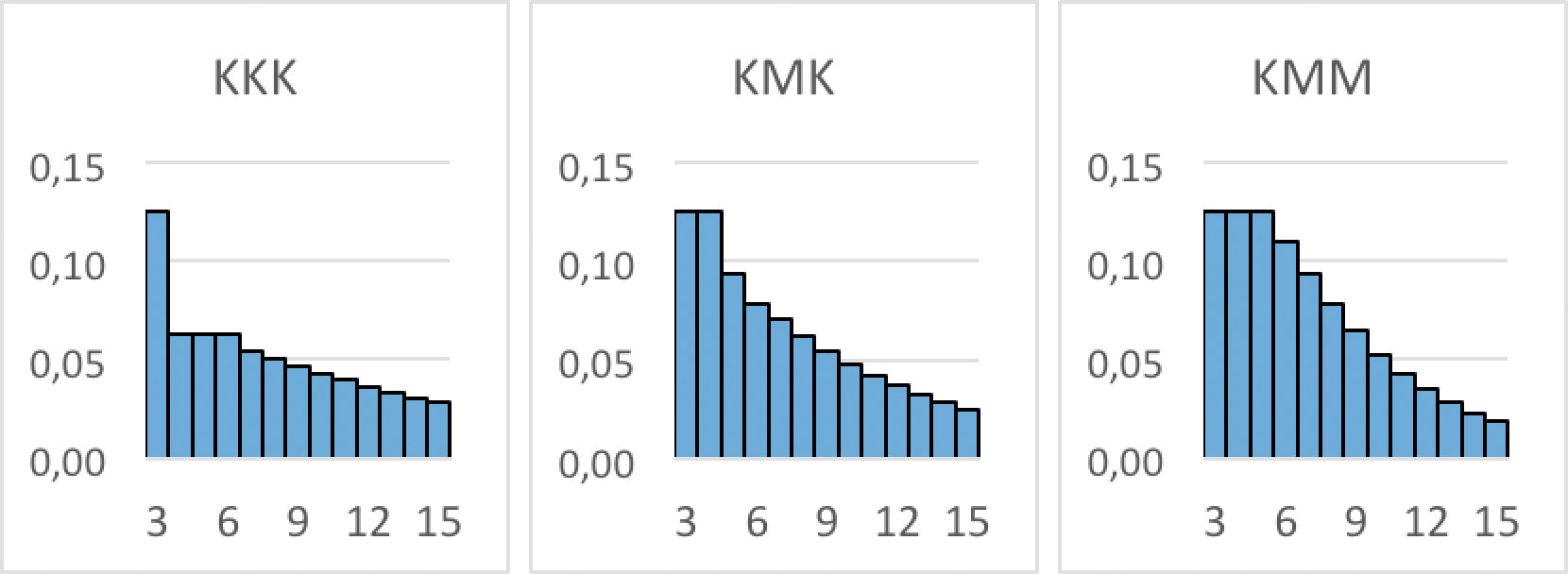
Ook hier hebben we te maken met drie groepen. De drie kansverdelingen zijn verschillend, maar de verschillen zijn niet spectaculair. Wel wordt duidelijk dat een wedstrijd lang kan duren. $\rm KMM$ valt gemiddeld na $8$ worpen, maar de kans dat het langer dan $14$ worpen duurt is ca $10\%$. Je zou ervoor kunnen kiezen om een maximaal aantal worpen af te spreken, met als mogelijke uitkomst: onbeslist.

We bekijken $\rm KKK$ (of $\rm MMM$) tegen $\rm KKM$ (of $\rm KMM$ of $\rm MMK$ of $\rm MKK$). In de tabel hieronder zien we de kansverdeling van alle mogelijke combinaties die we met bovenstaande kunnen berekenen. Gemakshalve zijn alle uitkomsten waarbij $\rm KKM$ het eerst valt oranje gekleurd, de combinaties waarbij $\rm KKK$ wint groen.

Figuur 2

	A>>	3	4	5	6	7	>7
C		0,1250	0,0625	0,0625	0,0625	0,0547	0,6328
3	0,1250	0,0156	0,0078	0,0078	0,0078	0,0068	0,0791
4	0,1250	0,0156	0,0078	0,0078	0,0078	0,0068	0,0791
5	0,1250	0,0156	0,0078	0,0078	0,0078	0,0068	0,0791
6	0,1094	00137	0,0068	0,0068	0,0068	0,0060	0,0692
7	0,0938	0,0117	0,0059	0,0059	0,0059	0,0051	0,0593
>7	0,4219	0,0527	0,0264	0,0264	0,0264	0,0231	0,2670

Dit levert de volgende resultaten:

	$\rm KKM$ wint		44%
	$\rm KKK$ wint		25%
	onbeslist		31%

$\rm KKM$ heeft dus een flink hogere kans om te winnen dan $\rm KKK$. De odds zijn ongeveer $7 : 4$, en dat lijkt aardig te kloppen met de verwachtingswaarden van het benodigde aantal worpen $(8 {\rm\ en\ } 14)$. Als we langer doorgaan met gooien, net zolang tot er een winnaar is, blijft de kansverhouding ongeveer, maar niet exact, $7:4$.

Als $\rm KKM$ het opneemt tegen $\rm KMK$ (of $\rm MKM$) is de overmacht , zoals ook te verwachten, minder groot: $\rm KKM$ wint nu in $40\%$ van de gevallen en $\rm MKM$ $33\%$. $27\%$ eindigt (bij maximaal $7$ worpen althans) in onbeslist. De odds zijn nu ongeveer $6:5$, en lijkt weer te kloppen met het gemiddeld aantal worpen dat nodig is, $8$ voor $\rm KKM$ en $10$ voor $\rm KMK$, hoewel sommigen wellicht de verhouding $5:4$ hadden verwacht.

Voor langere reeksen geldt iets dergelijks.

De reeks $\rm KKKKK$ komt, zoals in het de vorige stuk uitgelegd, gemiddeld na $2^6 - 2\ (= 62)$ worpen tevoorschijn. Bij $\rm KMMMM$ is dat al na $2^5\ (=  32)$ keer. Bij een wedstrijd tussen deze twee patronen blijken de winstkansen van $\rm KMMMM$ ongeveer $^2/_3$.

Wanneer je verwachtingswaarden van het gemiddeld aantal worpen kent kun je dus aardig je kansen inschatten. Tenminste als ieder zijn eigen munt gebruikt om te gooien. Wanneer er slechts één munt wordt gebruikt, wordt echter alles anders. Het gemiddeld aantal benodigde worpen blijkt dan ineens veel minder doorslaggevend, en tactisch spelen blijkt dan van essentieel belang.

Meer daarover in de volgende aflevering.