Is een reeks van vijf keer Kop qua waarschijnlijkheid ook echt gelijkwaardig met bijvoorbeeld de reeks KMKKM? Het antwoord op deze vraag is afhankelijk van wat precies bedoeld wordt, en biedt tal van verrassingen.

Een voor de hand liggende manier om na te gaan of KKKKK echt even vaak voorkomt als bijv. KMKKM is ‘domweg’ tellen hoe vaak deze reeksen voorkomen bij een groot aantal worpen (al dan niet gesimuleerd). Er doet zich meteen een probleem voor: naast reeksen van 5 opeenvolgende K’s zullen ook reeksen van 6, 7 of meer opeenvolgende K’s gevonden worden. Uiteraard moeten die ook meegeteld worden, maar hoe vaak?

Ter voorkoming van vaagheden in de vraagstelling wordt in dit soort zaken vaak gebruik gemaakt van bedachte spelsituaties en bijbehorende weddenschappen. Hierbij zijn naast berekeningen ook simulaties mogelijk om na te gaan wie aan het langste eind trekt.

In alle spellen wordt er net zolang met muntjes gegooid totdat een bepaald patroon wordt bereikt (bijvoorbeeld KKKKKK). Als er tegen elkaar wordt gespeeld is de winnaar degene van wie het patroon het eerst is geworpen.

We bekijken de volgende drie varianten

1. Er wordt tegen de bank gespeeld. Elke worp kost 1 euro, en als het patroon waarop is ingezet verschijnt, betaalt de bank een van tevoren bepaald bedrag uit.

2. Twee spelers spelen tegen elkaar. Iedere speler heeft zijn eigen munt, en ze mogen om beurten één worp doen.

3. Twee spelers spelen tegen elkaar. Er is maar één munt waarmee beurtelings wordt gegooid.

We kijken in dit artikel alleen naar spel 1. Om erin te komen beperken we ons eerst tot reeksen van 3, dus bijv. KKK of KMM.

 

Een handige berekening voor KKK

Voor KKK ziet de weg naar succes er als volgt uit:

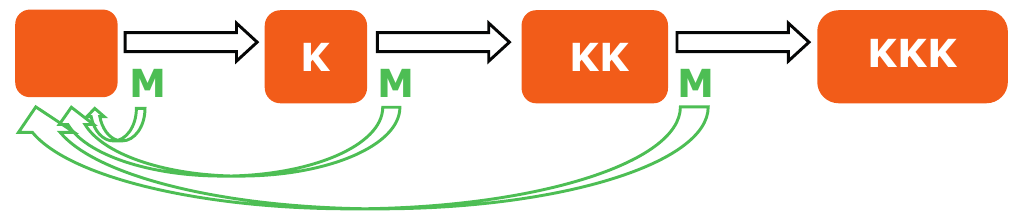
Je begint met net zolang werpen tot er kop boven komt. Wanneer dat is gelukt is de eerste stap gezet en staat het spel in de tussenstand K. Als de worp hierna weer K is komt het spel in tussenstand KK, maar als er munt wordt gegooid begint de hele zaak weer opnieuw. Als KK is bereikt is het nog één stap naar het eindresultaat, maar de kans is 50% dat je weer helemaal opnieuw moet beginnen.

We gaan berekenen hoeveel stappen er gemiddeld nodig zijn om vanuit niets de eindstand KKK te bereiken. Formeler uitgedrukt: we willen de verwachtingswaarde berekenen van het aantal benodigde worpen. We geven dit aantal benodigde worpen aan met $A$. We geven met $A_1$ het aantal stappen aan dat nodig is voor de eerste K, met $A_2$ het aantal stappen voor de tweede K en $A_3$ het aantal stappen voor de derde K. Uiteraard geldt $A = A_1 + A_2 + A_3$.

We delen dus het traject van ‘niets’ naar KKK op in drie delen, en gaan vervolgens van deze drie delen het gemiddeld aantal benodigde worpen bepalen. Kortheidshalve schrijven we voor de verwachting $E(A_i) : E_i$.

Voor de eerste stap (van 'niets' naar K) zijn gemiddeld 2 worpen nodig. Dat is op verschillende manieren te berekenen. Een handige manier werkt enigszins indirect. Je drukt de verwachtingswaarde van het aantal benodigde worpen voor de eerste stap uit in zichzelf! De redenering is als volgt: als je K gooit ben je in 1 stap klaar, als je munt gooit betekent het dat je teruggaat naar het begin en kost het één stap extra. Kort opgeschreven:

$$(1)\qquad E_1 = {1 \over 2} \times 1 + {1 \over 2} \times (1+E_1)$$

Vergelijking $(1)$ laat zich herschrijven als $2E_1 = 1 + (1 + E_1)$ en is eenvoudig op te lossen: $E_1 = 2$.

De berekening van de verwachtingswaarde voor het benodigde aantal worpen voor de tweede stap (van K naar KK) $E_2$ gaat bijna net zo. Nu wordt de verwachtingswaarde echter bij pech niet met 1 verhoogd, maar met 1 plus de verwachtingswaarde van het aantal benodigde worpen van het eerste stuk. In formulevorm:

\begin{eqnarray*}E_2 &=& {1 \over 2} \times 1 + {1 \over 2} \times (1 + E_1 + E_2) \Leftrightarrow\\2E_2 &=& 1 + (1 + E_1 + E_2) \Leftrightarrow\\E_2 &=& 2+E_1 = 2 + 2 = 4\end{eqnarray*}

Bij de berekening van $E_3$ wordt de aanpak nog wat duidelijker:

\begin{eqnarray*}E_3 &=& {1 \over 2} \times 1 + {1 \over 2} \times (1 + E_1 + E_2 + E_3) \Leftrightarrow\\2E_3 &=& 1 + (1 + E_1 + E_2 + E_3) \Leftrightarrow\\E_3 &=& 2+E_1+E_2 = 2 + 2 +4 = 8\end{eqnarray*}

Gelukkig kunnen we verwachtingswaarden (gemiddelden) gewoon optellen, dus het gemiddeld aantal worpen dat nodig is om KKK te bereiken is $E_1 + E_2 + E_3 = 2 + 4 + 8 = 14$. Als je nog eens goed naar de berekening van $E_1$ t/m $E_3$ kijkt zie je wellicht de volgende verbanden:

1. $E_i = 2 + E_1 + ⋯ + E_{i-1}$

2. $E_i = 2^i$

Dat het om echte regels gaat, die ook gelden voor langere reeksen, zoals KKKKKK, moet uiteraard bewezen worden. Dat kan door de berekening van $E_i \; (i > 3)$.

$$E_i = {1 \over 2} \times 1 + {1 \over 2} \times (1 + E_1 + ... + E_i) $$

Beide kanten keer $2$ levert:

\begin{eqnarray*}2 E_i &=& 2 + E_1 + … + E_i\\&&(-E_i \text{ aan beide kanten})\\E_i &=& 2 + E_1 + … + E_{i-1}\end{eqnarray*}

Hiermee is het eerste verband bewezen.

Het tweede volgt snel als we de eerste regel herschrijven als

$$E_{i+1} = 2 + E_1 + … + E_{i-1} + E_i$$

en vervolgens $2 + E_1 + … + E_{i-1}$ vervangen door $E_i$. Er staat nu $E_{i+1} = E_i + E_i (= 2 E_i)$. Omdat $E_1=2 (=2^1)$ zijn we klaar. Het gaat bij $E_i$ om een meetkundige (of zo je wilt exponentiële) rij met als eerste getal $2$, oftewel $E_i = 2^i$. Met deze kennis kunnen we de verwachtingswaarde van het aantal benodigde worpen voor een reeks van $5$ opeenvolgende worpen “kop” (KKKKK) bepalen:

\begin{eqnarray*}E_1 &=& 2; \; E_2 = 2^2 = 4; \; E_3 = 2^3 = 8;\\E_4 &=& 2^4 = 16; \; E_5 = 2^5 = 32;\\E &=& 2 + 4 + 8 + 16 + 32 = 62.\end{eqnarray*}

In het algemeen geldt voor het gemiddeld aantal worpen dat nodig is om een reeks van $n$ keer kop te krijgen:

$$E = \sum_{i=1}^n 2^i = 2 + 2^2 + 2^3 + … + 2^n = 2^{n + 1} – 2$$

 

Andere samenstellingen

Hoe zit dat voor een reeks met een wat meer gemengde samenstelling?

We bekijken de situatie voor KMM:

Evenals bij KKK geldt $E_1 = \frac12 \times 1 + \frac12 \times (1 + E_1) \Leftrightarrow 2E_1 = 1 + (1 + E_1) \Leftrightarrow E_1 = 2$. Het gemiddeld aantal worpen voor de eerste stap is altijd $2$. Maar daarna zien de vergelijkingen er iets anders uit dan bij KKK. Het gaat bij $E_2$ namelijk om de situatie KM… of KKM…, en bij $E_3$ om de situatie KMM… of KMKMM… .

\begin{eqnarray*}E_2 &=& \frac12 \times 1 + \frac12 \times (1 + E_2) \Leftrightarrow\\2E_2 &=& 2 + E_2\Leftrightarrow\\E_2 &=& 2.\\E_3 &=& \frac12 \times 1 + \frac12 \times (1 + E_2 + E_3) \Leftrightarrow\\2E_3 &=& 1 + (1 + E_2 + E_3) \Leftrightarrow\\E_3 &=& 2 + E_2 = 4.\end{eqnarray*}

Hieruit volgt $E_3 = 2 + 2 = 4$ en $E = 2 + 2 + 4 = 8$. Het aantal worpen dat gemiddeld nodig is om KMM ligt dus een stuk lager dan bij KKK. In het algemeen geldt voor een reeks die bestaat uit KM...M ($n – 1$ keer M) dat

$$E = 2 + \sum_{i=1}^{n-1} 2^i = 2 + 2^n - 2 = 2^n.$$

Een reeks van K gevolgd door $4$ keer M heeft dus gemiddeld $2^5 (=32)$ worpen nodig, $1$ meer dan de helft van het aantal worpen dat gemiddeld nodig is voor KKKKK. Een verwachtingswaarde van $2^n$ blijkt ook het minimum te zijn voor een reeks met lengte $n$. Bij een reeks als KMKKM ligt het gemiddeld aantal benodigde worpen ergens tussen $2^n$ en $2^{n+1} – 2$.

De bijbehorende keten ziet er zo uit:

We kunnen de verwachtingswaarden van de $5$ tussenstappen op eenzelfde manier berekenen als bij de reeksen met lengte $3$, maar de volgende aanpak is iets sneller.

Met $O_i$ bedoelen we de verwachtingswaarde van het aantal benodigde worpen dat extra nodig is wanneer de stap van toestand $T_{i-1}$ naar toestand $T_i$ niet lukt. Denk bij $O$ aan ‘omweg’.

Kijkend naar de keten zien we $O_1 = O_2 =0$; $O_3 = E_1 + E_2$; $O_4 = E_3$; $O_5 = E_2 + E_3 + E_4$. Een regel die geldt voor elke reeks is: $E_i = 2 + O_i$. In woorden:

De verwachtingswaarde van het aantal benodigde worpen voor een stap is gelijk aan 2 plus de som van de verwachtingswaarden van de omweg die noodzakelijk is wanneer de volgende tussenstand niet direct wordt bereikt.

We kunnen nu de verwachtingswaarden van de stappen redelijk snel berekenen:

1. $E_1 = 2$

2. $E_2 = 2 + 0 = 2$

3. $E_3 = 2 + E_1 + E_2 = 6$

4. $E_4 = 2 + E_3 = 8$

5. $E_5 = 2 + E_2 + E_3 + E_4 = 18$

Optellen geeft $E = 36$ voor KMKKM, en dat is vier meer dan bij de reeks KMMMM.

 

KMM toch eerder dan KKK

Uit bovenstaande berekening blijkt dat een rijtje van gemengde samenstelling toch eerder voorkomt dan een rijtje met de hele tijd kop. Wellicht dat daar je gevoel vandaan komt dat drie keer kop gooien minder vaak voorkomt dan kop - munt - munt. Het ligt er dus maar helemaal aan wat het exacte experiment is waar je naar kijkt. Het is leuk om hiermee een winnend spel te bedenken bijvoorbeeld voor in de kantine of om je wiskundeleraar uit te dagen!