Voordat we beginnen met de uitleg hoe je zélf een 3D-tekening maakt, is het van belang precies te begrijpen hoe zo'n tekening in elkaar steekt. Daar heeft het standpunt van de beschouwer alles mee te maken. Stel dat ik een kubus wil tekenen en deze midden op een plein wil positioneren. Dan maakt het enorm veel uit vanuit welke hoek de beschouwer kijkt: de persoon links ziet de kubus tenslotte vanuit een heel andere hoek dan de persoon rechts.

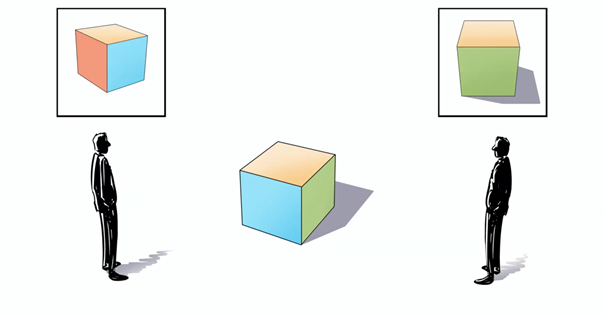$\color{RoyalBlue}{Figuur\ 1}$ De beschouwer links ziet een ander deel van de kubus dan de beschouwer rechts.

Het is dan ook van belang om vóórdat je de tekening begint eerst het standpunt te bepalen van de kijker. In dit voorbeeld kiezen we voor de beschouwer links in beeld. Als we voor deze persoon de acht hoekpunten van de kubus op de grond willen construeren, dan valt direct op dat de onderste vier hoekpunten al op de grond liggen.

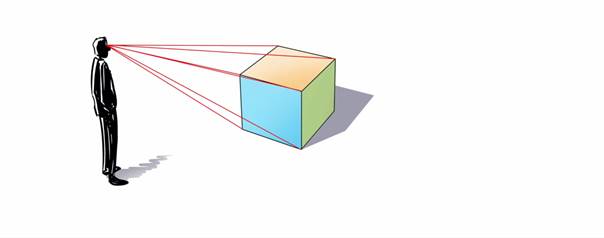$\color{RoyalBlue}{Figuur\ 2}$ De vier hoekpunten aan de onderzijde van de kubus bevinden zich al op de grond.

Als we de bovenste vier hoekpunten op het platte vlak willen projecteren, dan moeten we de kijklijn van de beschouwer naar de vier hoekpunten doortrekken tot aan het grondoppervlak.

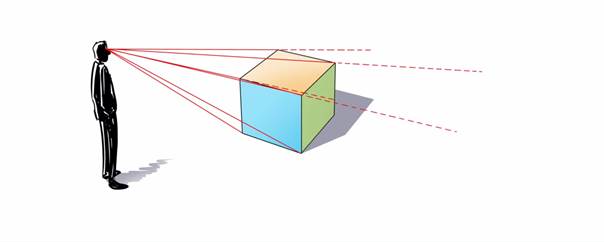$\color{RoyalBlue}{Figuur\ 3}$ De lijnen vanuit het oog van de beschouwer naar de vier hoekpunten worden doorgetrokken naar het grondoppervlak.

Wanneer we ook deze vier hoekpunten hebben geconstrueerd kunnen we die bovenste vier hoekpunten met een rechte lijn verbinden met de overeenkomstige hoekpunten van het grondvlak. Dan valt er iets op: die lijnen (de projecties van de verticale ribben) komen, als je ze verlengt, samen bij het standpunt van de beschouwer.

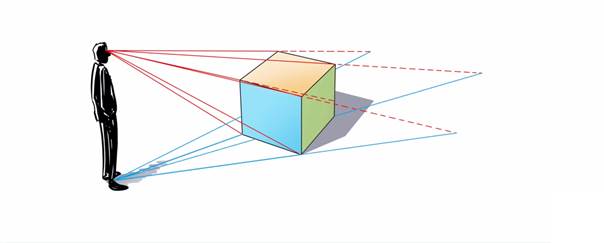$\color{RoyalBlue}{Figuur\ 4}$ Alle verticale lijnen komen samen op de plek waar de beschouwer staat.

Als we vervolgens de kubus verder uittekenen tot een complete straattekening is dit de tekening waar de kijker links een echte, driedimensionale kubus in zal zien.

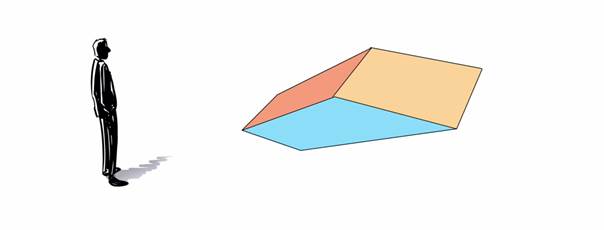$\color{RoyalBlue}{Figuur\ 5}$ De straattekening van een kubus voor de beschouwer links.

VertiCale lijnstukken berekenen

Aangezien we voor het maken van een échte straattekening geen gebruik kunnen maken van denkbeeldige lijnen vanuit het oogpunt van de beschouwer, zijn we gedwongen om uit te rekenen hoe lang de gewenste verticale lijnen moeten zijn. Om dit te kunnen doen maken we gebruik van een zijaanzicht. In dit voorbeeld tekenen we een dobbelsteen met ribben van ieder $40$ centimeter, zie figuur 6.

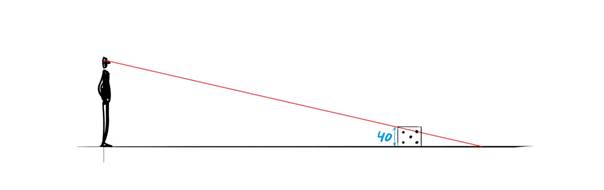$\color{RoyalBlue}{Figuur\ 6}$ De beschouwer kijkt naar de gewenste dobbelsteen.

Om de lengte van de projectie van de voorste verticale ribbe te bepalen moeten we op zoek naar de variabelen waarvan we de waarden wél kennen. In dit voorbeeld kiezen we voor een afstand van $580$ cm van de beschouwer tot de voorste ribbe van de dobbelsteen. Aangezien ook de kijkhoogte van de beschouwer van invloed is op de lengte van de projectie van de ribbe, stellen we deze van tevoren vast op de gemiddelde kijkhoogte van Nederlanders. Deze is ongeveer $170$ centimeter, zie figuur 7.

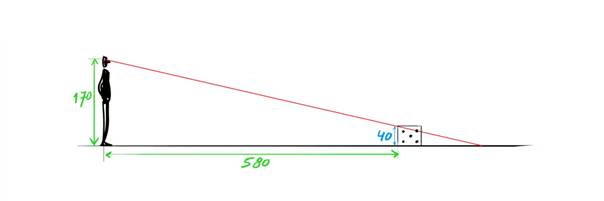$\color{RoyalBlue}{Figuur\ 7}$ De kijkhoogte en de afstand tot de dobbelsteen zijn van tevoren bepaald.

Wat in dit zijaanzicht opvalt is dat hier twee gelijkvormige driehoeken te vinden zijn, namelijk een grote driehoek en een kleine driehoek. Om de lengte van een willekeurig verticaal lijnstuk te vinden, maken we nu gebruik van deze gelijkvormigheid.

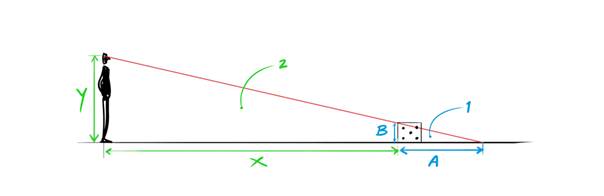
		Gelijkvormige driehoeken Wanneer we in onderstaande situatie de lengte van lijnstuk A willen bepalen, berekenen we dit met behulp van de gelijkvormigheid van de driehoeken 1 en 2. Zie figuur 8. $\color{RoyalBlue}{Figuur\ 8}$ Twee gelijkvormige driehoeken Voor ieder lijnstuk A kan de volgende vergelijking worden opgemaakt: $$\frac{A}{B}=\frac{X+A}{Y}$$ Aangezien dit een vergelijking is met slechts één onbekende A, kan A worden berekend met de volgende herleide formule: $$A=\frac{BX}{Y-B}$$

In het voorbeeld van figuur 7 resulteert dit in een lengte van het verticale lijnstuk van $178$ cm. Dit is overigens ruim vier (!) keer zo lang als de ribben van het oorspronkelijke grondvlak. Tegelijkertijd is dit goed voor te stellen wanneer de beschouwer ver weg staat. Wanneer we deze berekening herhalen voor de andere drie verticale lijnstukken, leidt dit tot een exact vierkant oppervlak: het bovenste vlak van de kubus.

Construeren van Cilinders

Voor deze laatste uitleg beperken we ons tot het construeren van een staande cilinder. Daarbij schetsen we, net als bij de dobbelsteen, eerst het grondvlak op de plek waar we de cilinder willen plaatsen. Dit grondvlak is exact een cirkel Zie figuur 9.

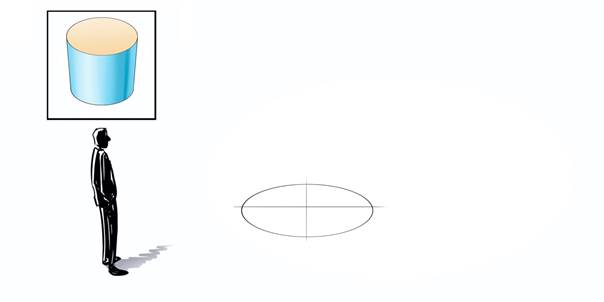$\color{RoyalBlue}{Figuur\ 9}$ De beschouwer kijkt naar het grondvlak van de cilinder.

Alle verticale lijnen komen wederom samen op de plek waar de kijker staat. In het geval van een cirkel als grondvlak zijn de lijnen links en rechts van de cilinder raaklijnen van het grondvlak. De derde lijn vanuit de beschouwer is de middellijn die het middelpunt van de cirkel precies doorkruist. Zie figuur 10.

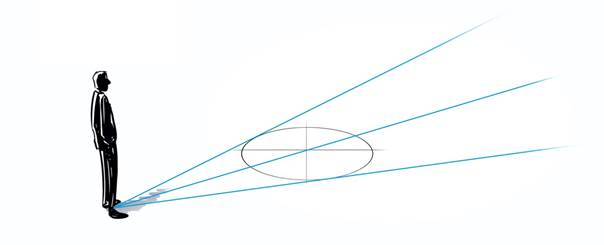$\color{RoyalBlue}{Figuur\ 10}$ Raaklijnen van het grondvlak van de cilinder

Vervolgens gebruiken we de berekening uit het kader 'gelijkvormige driehoeken' om de lengte van de verticale lijnstukken te berekenen. Om het middelpunt van het bovenvlak van de cilinder te bepalen, gebruiken we het gegeven dat de twee verticale lijnstukken ook de raaklijnen van het bovenvlak zijn. Daarom tekenen we nu een lijn loodrecht van één van de twee verticale lijnen naar de middellijn. Het punt waar ze elkaar kruisen vormt het middelpunt van het cirkelvormige bovenvlak. Zie figuur 11.

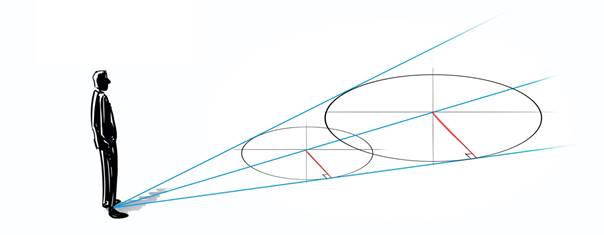$\color{RoyalBlue}{Figuur\ 11}$ De verticale lijn rechts is een raaklijn voor zowel het grondvlak als het bovenvlak.

Met het construeren van het bovenvlak is de volledige cilinder geschetst. Zie figuur 12.

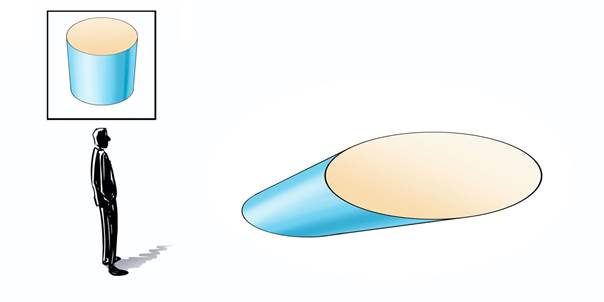$\color{RoyalBlue}{Figuur\ 12}$ De cilinder geconstrueerd voor de beschouwer links.