We beginnen met een wedstrijd tussen de priemen die een viervoud $\mbox{plus 1}$ en een viervoud ${\rm plus\ }3$ zijn. Dat kunnen we doen op grond van de observatie dat afgezien van het kleinste priemgetal $(2)$ elk priemgetal te schrijven is als veelvoud van $4 {\rm\ plus\ } 1$ of veelvoud van $4 {\rm\ plus\ } 3$.

Hierna zullen we spreken over Team 1 en Team 3; Team 1 telt de priemgetallen die een veelvoud van $4 {\rm\ plus\ } 1$ zijn en Team 3 telt de priemgetallen die een veelvoud van $4 {\rm\ plus\ } 3$ zijn. Team 3 gaat direct aan kop nadat we $3$ passeren, maar bij $5$ komen de teams weer naast elkaar te liggen. Maar dan neemt Team 3 een enorme voorsprong d.m.v. $7$ en $11.$ Team 1 maakt die voorsprong weer goed met $13$ en $17.$ De stand is nu 3 - 3. Hoe gaat het daarna? We hebben het verder in het artikel over een getal $N$. Als de teams 1 en 3 $N$ passeren dan wordt gekeken hoe groot Team 1 en Team 3 zijn. De winnaar op dat ogenblik is het grootste team.

Het is een interessante strijd die Team 1 en Team 3 leveren. Er valt van alles aan te programmeren. Mogelijk vindt je het leuk om met de hulp van de tools die we in de vorige nummer(s) hebben laten zien zelf aan de slag te gaan. Zo niet dan vind je de code op de site.

1. Hoe is de situatie voor Team 1 en Team 3 bij 100?
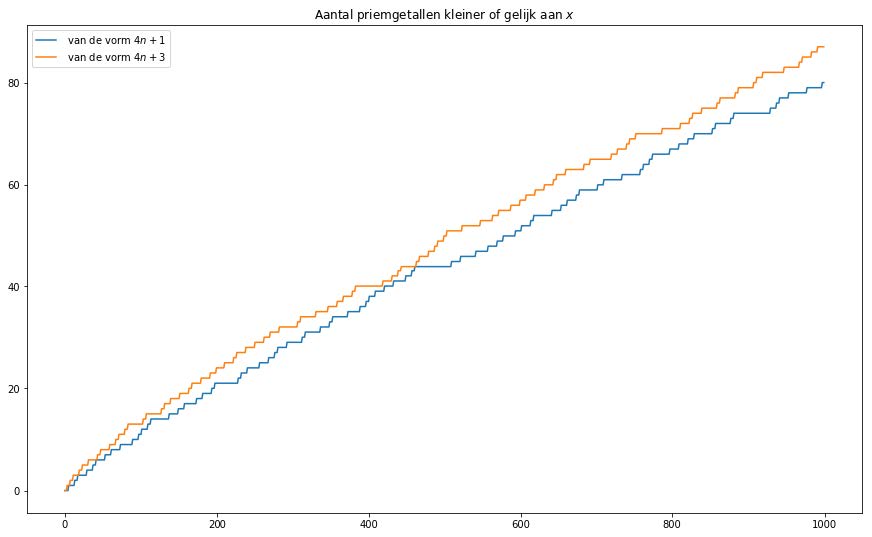
2. We gaan een plot maken voor Team 1 en Team 3. Daartoe schrijven we eerst een functie die de scores voor Team 1 en Team 3 bij $N$ bijhoudt. Wat zie je als je deze twee functies plot, voor tussen $1$ en $1000$ (of een groter getal)?

We zien dat Team 3 meestal op kop gaat, maar de voorsprong is niet zo gek groot (zie figuur 1). We weten dat er oneindig veel priemgetallen zijn. Maar we vragen ons sowieso af of er oneindig veel priemgetallen zijn voor Team 1 en Team 3? We doen het gemakkelijke deel eerst, en dat is Team 3. Team 3 wordt uiteindelijk oneindig groot.

Het bewijs is heel eenvoudig en is gebaseerd op het bewijs dat Euclides leverde, zoals we in de laatste aflevering ook al zagen. Stel dat het aantal priemgetallen voor Team 3 slechts eindig is. Dan kunnen we al deze getallen met elkaar vermenigvuldigen en komen uit op $P_3.$ $P_3$ is een viervoud ${\rm plus\ } 1$ of ${\rm plus\ } 3.$ Tel er vervolgens $2$ of $4$ bij op, zodat we opnieuw een viervoud ${\rm plus\ } 3$ hebben. Dit getal $M_3$ hoeft geen priemgetal te zijn. Zeker niet, want dan hadden we niet alle priemgetallen met elkaar vermenigvuldigd. OK, dan factoriseren we dit getal. Als $M_3$ louter factoren uit Team 1 bevat dan is dat product ook een viervoud ${\rm plus\ } 1.$ Maar $M_3$ is een viervoud ${\rm plus\ } 3.$ Daarom moet $M_3$ minimaal een priemgetal van Team 3 bevatten, waarvan we verondersteld hadden dat er slechts een eindig aantal van waren. En dan hebben we de tegenstrijdigheid. De priemgetallen uit Team 3 komen niet in aanmerking, immers $P_3 = M_3 - 2$ (of $P_3 = M_3 - 4)$ bevat al deze priemgetallen al als factor.

Dan is er uiteraard de vraag of er oneindig veel priemgetallen zijn voor Team 1. Het bewijs is een stuk lastiger. Want we kunnen al deze priemgetallen met elkaar vermenigvuldigen $(P_1)$ en er $4$ bij optellen. Maar het probleem is dat dit niet een priemgetal hoeft te zijn of een priemfactor uit Team 1 hoeft te bevatten. Dat zie je direct als je kijkt naar de eerste twee leden van Team 1: $5 \cdot 13 + 4 = 3 \cdot 23.$ Dat gaat helemaal mis.

Maar nu maken we gebruik van de kennis die we hebben over getallen die te schrijven zijn als som van twee kwadraten (zie Pythagoras 55-1, pagina 22). Voor elk oneven getal $T$ dat te schrijven is als som van twee kwadraten, zeg $T = a^2 + b^2,$ geldt dat $T$ te schrijven is als een product van priemgetallen van Team 1 en Team 3 (tot zekere machten). Maar de priemgetallen van Team 3 komen in $T$ altijd in even machten voor. Bovendien zijn de priemgetallen van Team 3 tevens delers van zowel $a$ als $b.$

Daar maken we gebruik van. Stel dat het aantal priemgetallen voor Team 1 eindig is. We nemen nu het product van deze priemgetallen $P_1$ en bekijken $M_1 = P_1^2 + 4.$ We zien direct dat dit een som is van twee kwadraten. Dit getal is zelf een priemgetal of het is een product van priemgetallen uit Team 1. Maar het is niet mogelijk dat daarbij de priemgetallen betrokken zijn die we met elkaar hebben vermenigvuldigd. Zodoende moet de veronderstelling dat er slechts eindig veel priemgetallen zijn die een viervoud ${\rm plus\ } 1$ zijn onjuist zijn.

Met deze kennis gaan we kijken naar hoe Team 1 en Team 3 zich gedragen voor grotere waarden. We kiezen voor een grens van 2 miljoen. We gaan om te beginnen kijken in hoeverre de grootte van Team 1 gelijk opgaat met de grootte van Team 3. Het programma staat op de site. Mogelijk vind je het leuk om eerst zelf eens te proberen of je het programma kunt bedenken.

Het blijkt dat de verschillen niet zo groot zijn: Tot 2 miljoen kan de winst voor Team 1 oplopen tot $24$ en die voor Team 3 tot $574,$ maar zelfs dit is minder dan 1 promille.

Vervolgens gaan we een grafiek maken waarin we het verschil Team 3 – Team 1 uitzetten tegen het aantal priemgetallen. Probeer of je dit zelf voor elkaar kunt krijgen. Op de webpagina kun je het programma terugvinden. In figuur 2 staat het resultaat.

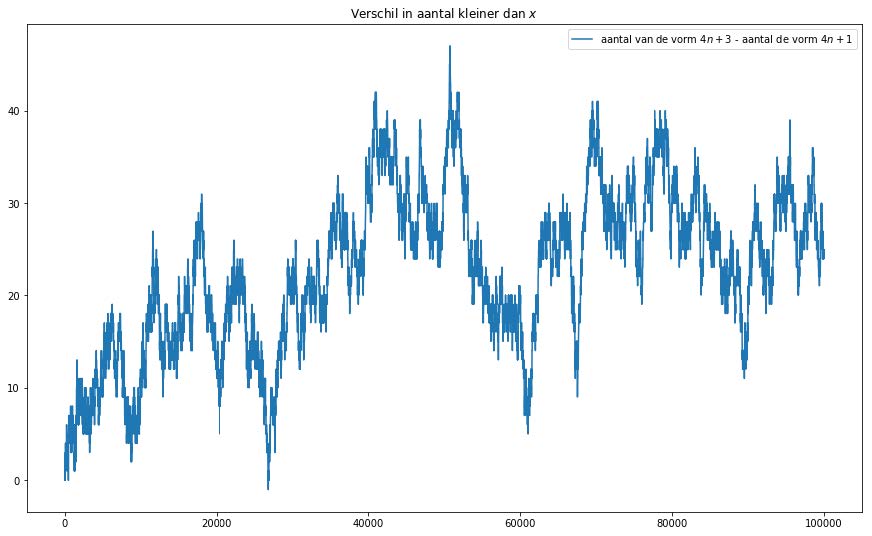
Resultaten koers Team 1 en Team 3

Tot het 2 miljoenste priemgetal (32452867):

• Maximale winst Team 1: 24
• Maximale winst Team 3 : 574

Als je boven het 2 miljoenste priemgetal komt dan zie je dat de winst voor Team 1 in relatief kleine intervallen ligt. Dit zijn de kleinste intervallen:

• van 26.861 tot 26.861
• van 616.841 tot 633.797
• van 12.306.137 tot 12.382.313
• van 951.784.481 tot 952.223.501
• van 6.309.280.697 tot 6.403.150.361
• van 18.465.126.217 tot 19.033.524.537

Veelvouden van 3 plus 1 en plus 2 en generalisatie

Tot nu toe hebben we alleen de wedstrijd bekeken tussen Team 1 en Team 3 waarbij de teams strijden als veelvouden van $4 \mbox{ plus een rest.}$ Maar een hele interessante wedstrijd ontstaat als de teams Team 1 en Team 2 het tegen elkaar opnemen als veelvouden van $3 \mbox{ plus 1}$ en $\mbox{ plus 2.}$ Het bijzondere nu is dat Team 2 gedurende lange tijd op winst staat. Betekent dit dat er maar eindig veel priemgetallen behoren tot Team 1? Nee zeker niet! Met vergelijkbare methodes als hierboven is na te gaan dat er oneindig veel priemgetallen behoren tot Team 1 (net als Team 2).

Het is slechts schijn dat Team 2 het altijd beter doet dan Team 1. Alleen: voor een omslagpunt moet je nu gaan tot $608.981.813.029.$

We kunnen zo doorgaan en kijken naar $N\mbox{-vouden plus 1}$ en $N\mbox{-vouden min 1.}$ Hoe is het dan gesteld met de wedstrijd van team 1 tegen Team $N-$1?

Het blijkt dat Team 1 meestal direct op achterstand staat.

De rij 608981813029, 26861, 11, 608981813017, 71, 192252423729713, 37, 11, 23 (zie oeis.org/A275939) geeft weer wanneer Team 1 voor het eerst op winst staat.

Als voor de getallen $a, b$ en $c$ geldt dat $a$ en $b$ geen gemeenschappelijke priemdelers hebben en $a$ en $c$ evenmin, dan kunnen we de teams B en C beschouwen, bestaande uit respectievelijk de getallen $B = \{b + ka\}$ en $C = \{c + ka\}.$ Er zal gelden dat de teams B en C bij benadering evenveel priemgetallen bevatten. Als je een prachtig, maar wel behoorlijk pittig, stuk hierover wilt lezen dan is de introductie van Prime Number Races van Andrew Granville en Greg Martin een aanrader.

Niets weerhoudt je om meerdere teams tegen elkaar te laten spelen. Bijvoorbeeld met $a = 30$ kun je de teams 1, 7, 11, 13, 17, 19, 23 en 29 laten spelen. Hoe verloopt nu de wedstrijd? Je zult zien dat de teams redelijk gelijk op gaan.

De Python code behorende bij dit artikel krijg je door op de knop "Bekijk oplossing" te klikken. De code is ook te vinden in het bijgevoegde pdf-document.

Bekijk oplossing