De opgave In scherphoekige driehoek $ABC$ met $|BC| < |BA|$ is $N$ het midden van $AC$. De cirkel met middellijn $AB$ snijdt de bissectrice van $\angle B$ in twee punten: $B$ en $X$. Bewijs dat XN evenwijdig is met BC.

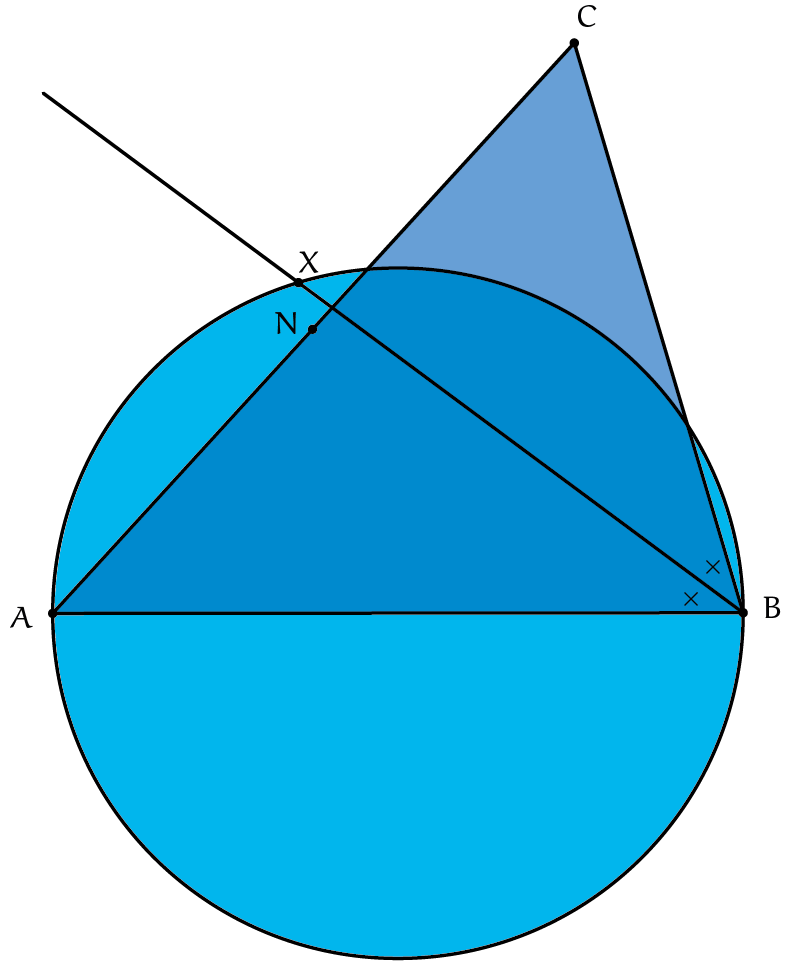De vraagstelling is kort maar krachtig: met slechts vijf punten wordt toch een pittige opgave neergezet. Als we een meetkundevraag op willen lossen met zo weinig gegeven punten, zijn er een paar strategieën die elke finalist vooruit kunnen helpen:

• Bekijk het gegeven plaatje aandachtig en kijk zo of er stukjes informatie over de configuratie te vinden zijn.
• Trek lijnen door of introduceer nieuwe, tactisch gekozen punten. Zorg altijd dat er een gedachte achter het doortrekken of het introduceren zit, om concreet naar vermoedens te kunnen zoeken. Zo kan een rechthoekige driehoek motiveren tot het gebruiken van de stelling van Pythagoras of kunnen hoekengelijkheden motiveren tot het zoeken naar gelijkvormigheden.
• Als je het plaatje aandachtig hebt bestudeerd en de gevonden informatie nog niet genoeg inzicht geeft, kun je een tweede of derde plaatje tekenen om nieuwe vermoedens te vinden of al gevonden vermoedens te controleren.

In het gegeven plaatje zien we nog niet echt iets opmerkelijks, dus laten we een lijn doortrekken of een nieuw punt introduceren. Een lijn die logisch lijkt om te tekenen is $XN$, aangezien de opgave draait om het bewijzen van de evenwijdigheid van $BC$ en $XN$. We kunnen nu verder zoeken naar stukjes informatie verstopt in de opgave.

Het is handig om als vuistregel altijd even te kijken wat elk onderdeel van de vraag inhoudt, ook al komt er niet direct iets uit, zodat je het ten minste al een keer hebt gezien. Vaak is de opgave niet oplosbaar als je iets wat gegeven was niet gebruikt, dus probeer dat koste wat het kost te voorkomen.

Als we nu alle gegevens van de vraag afgaan, zien we dat er nog best wat informatie verstopt is. Zo ligt $X$ op de cirkel met middellijn $AB$. Het feit dat de cirkel middellijn $AB$ heeft, betekent onder andere dat het midden van $AB$ het middelpunt van de cirkel is. Omdat dit punt het middelpunt van de omgeschreven cirkel van $\Delta ABX$ is, geldt ook dat de afstand vanaf dat punt tot $B$ gelijk is aan de afstand tot $X$, wat een gelijkbenige driehoek geeft. Dat lijkt heel handig, dus het lijkt een goed idee te zijn om het midden van $AB$ te introduceren. We mogen dit punt elke naam geven die we maar willen, maar de naam $M$ is in dit geval passend.

Zelf heb ik tijdens de wedstrijd het punt $M$ geïntroduceerd omdat $N$ het midden van $AC$ is. Door $M$ te introduceren als het midden van $AB$, hebben we twee middens van lijnstukken in één driehoek. Hier kunnen we veel meer mee dan met één midden, omdat we met twee middens al snel gelijkvormige driehoeken kunnen vinden, waarbij twee paar zijdes de verhouding $1 : 2$ hebben en de ingesloten hoek gelijk is. Daarnaast leek het alsof $XN$ het lijnstuk $AB$ middendoor snijdt. Dat vond ik ook bijzonder en gaf des te meer reden om $M$ te introduceren.

Ten slotte zien we nog dat $X$ op de bissectrice van $\angle ABC$ ligt, dus $\angle XBC = \angle XBA$. Nu zijn we door alle gegevens van de vraag heen gegaan en kunnen we met de andere strategieën aan de slag in het nieuwe plaatje. 

RiChting de oplossing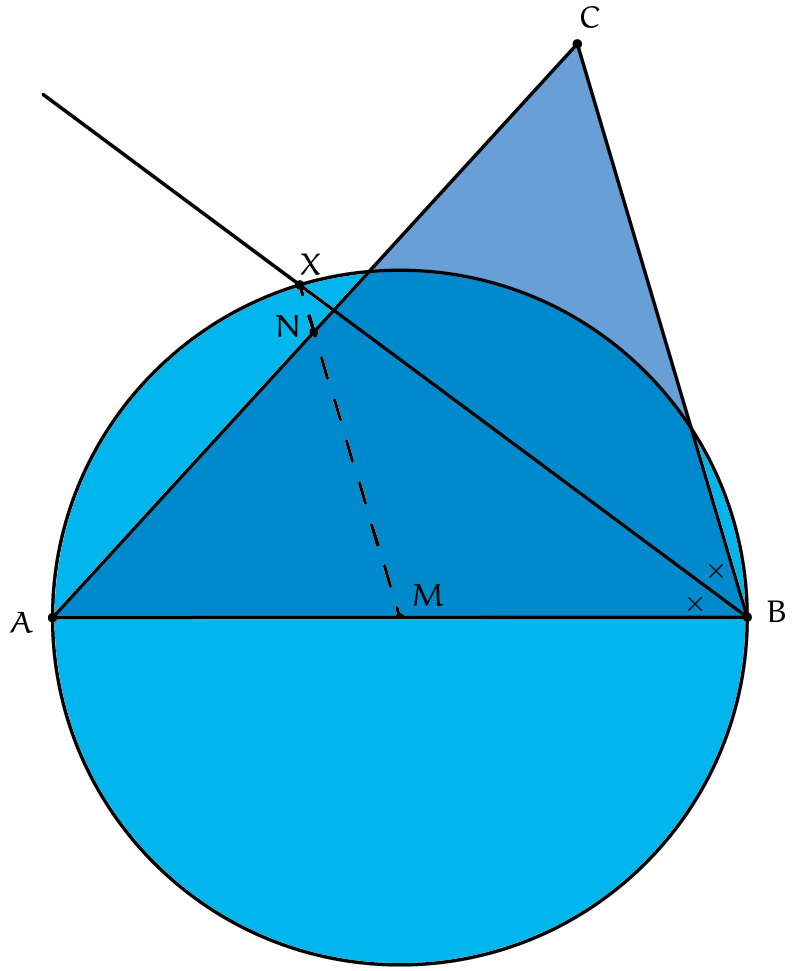

Als we kijken naar ons plaatje, nadat we het punt $M$ geïntroduceerd hebben, zien we dat het lijkt alsof $X$, $M$ en $N$ op een lijn liggen. In de afbeelding is dat aangegeven met een stippellijn, omdat we het nog niet zeker weten. Dat spoort ons aan om nu ook nog naar de lijnen $XM$ en $MN$ te kijken. Als het ons lukt om te bewijzen dat de drie punten $X$, $M$ en $N$ op een lijn evenwijdig met $BC$ liggen, dan krijgen we direct dat $XN$ evenwijdig met $BC$ is.

Laten we nu dus eerst naar lijn $MN$ kijken. We zien dat $M$ en $N$ de middens zijn van zijden van $\Delta ABC$. Er geldt dat

$\frac{|AM|}{|AB|}=\frac{1}{2}$ en $\frac{|AN|}{|AC|}=\frac{1}{2}$, zodat $\frac{|AM|}{|AB|}=\frac{|AN|}{|AC|}$.

Omdat $M$ op $AB$ ligt en $N$ op $AC$, krijgen we
ook nog dat +BAC = +MAN . Als we dit allemaal
samenpakken, krijgen we:

$\frac{|AM|}{|AB|}=\frac{|AN|}{|AC|}$

$\angle MAN = \angle BAC$

wat samen, volgens het gelijkvormigheidsgeval zijde-hoek-zijde, geeft dat $\Delta MAN$ gelijkvormig is met $\Delta BAC$.

Dit is erg handig, want daaruit volgt dat $\angle AMN = \angle ABC$. Met $F$-hoeken geeft dit dat $MN$ en $BC$ evenwijdig aan elkaar
zijn!

Vervolgens willen we kijken of $MX$ evenwijdig is met $BC$.

We zien dat $X$ en 4B op een cirkel liggen met middelpunt $M$, dus $\Delta MXB$ is gelijkbenig met tophoek $M$. Hieruit volgt dat

$$\angle MXB = \angle MBX = \angle XBC.$$

Al met al krijgen we dat $\angle MXB = \angle XBC$. Hier herkennen we Z-hoeken, die ons inderdaad vertellen dat $MX$ evenwijdig is met $BC$.

Laatste loodjes

Als we kijken naar onze lijnen $MX$ en $MN$, beide evenwijdig aan $BC$, zien we dat zij onderling ook evenwijdig moeten zijn. We hebben nu twee evenwijdige lijnen, die beide door het punt $M$ gaan. Dit betekent dat het dezelfde lijn is. Daarom liggen $M$, $X$, $N$ op een lijn. Omdat deze lijn evenwijdig is aan $BC$, is in het bijzonder ook $XN$ parallel aan $BC$, precies wat we wilden bewijzen!

Samengevat

Kortom: bij een algemene meetkundeopgave is er een aantal standaardstrategieën waarmee iedereen al een goed begin kan maken. Het goed volgen van een logisch plan geeft veel inzicht in de configuratie zelf, maar ook in wat er precies bewezen moet worden en hoe dat in verhouding staat tot de rest van de opgave. Ook is er natuurlijk wat intuïtie en creativiteit nodig om te zien wanneer welke stappen gezet moeten worden, zoals bij het zoeken naar gegevens in de opgave. Door handig te kiezen wat je wanneer bekijkt, ontstaat er een natuur- lijke flow die je gedurende de opgave op weg helpt naar het volgende idee. Zo val je met je ideeën al binnen de kortste keren in de punten voor een gedeeltelijke oplossing of vind je zelfs een complete oplossing.