W4KangoerOE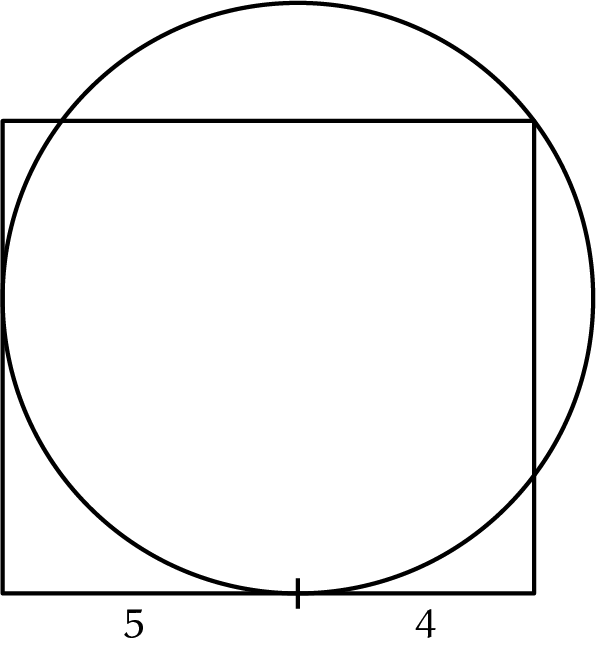

(W4kangoeroe.nl)

We hebben een rechthoek en een cirkel die twee zijden van de rechthoek raakt en door een hoekpunt gaat, zoals weergegeven in de figuur hiernaast. Een van de raakpunten bevindt zich op een afstand 5 respectievelijk 4 van de aangrenzende hoekpunten van de rechthoek. Wat is de oppervlakte van de rechthoek?

A $27\pi$

B $25\pi$

C $72$

D $63$

E ander antwoord

Twee hardlopers trainen op een ronde baan van $720$ meter. Beiden lopen met een constante snelheid. De eerste loper rent met de klok mee en loopt een ronde in $4$ minuten. De tweede rent tegen de klok in en loopt een ronde in $5$ minuten. De twee komen elkaar een aantal keer tegen. 

Hoeveel meter loopt de tweede hardloper tussen twee ontmoetingen in?

A $320$

B $330$

C $340$

D $350$

E $355$

 Sudoku

(Wil Schilders)

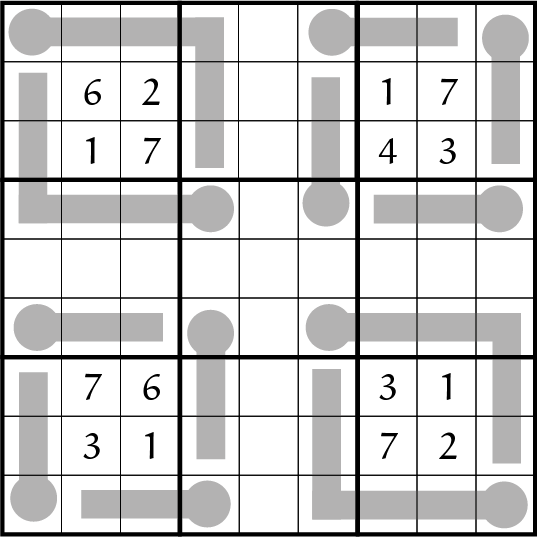
Een verrassende variant zijn de zogenaamde thermosudoku's die een aantal jaren geleden zijn bedacht voor een wereldkampioenschap. Hierbij zijn in het normale 9×9 sudoku diagram een aantal thermometers getekend, en de regel is dat de cijfers in die thermometer oplopend zijn. De "onderkant" van de thermometer, feitelijk overeenkomend met het kwikreservoir in een echte thermometer, wordt aangegeven met een grijs cirkeltje, en de rest van de thermometer wordt aangegeven met een dikke blauwe lijn. Het cijfer in het grijze cirkeltje is dan dus het laagste cijfer in die thermometer, en de cijfers op de dikke grijze lijn moeten dan steeds groter
worden. Overigens kunnen de thermometers hoekjes omgaan.

 Constructiepuzzel

(Maarten Löffler)

De getallen naast het diagram geven aan hoeveel delen van planken er op elke rij komen. Een plank bestaat uit één of meerdere plankdelen, en moet aan beide uiteinden worden bevestigd met een ketting (aan een hoger gelegen plank) of met een paal (aan een lager gelegen plank). Kettingen en palen bestaan ook uit één of meerdere delen; de getallen boven het diagram geven aan hoeveel kettingdelen er in hun kolom komen, en de getallen onder het diagram geven aan hoeveel paaldelen er in hun kolom komen. Twee planken zijn al gegeven: de vloer en het plafond.

Stabiliteit

Elke plank moet stabiel zijn. We definiëren stabiliteit recursief:

• De vloer en het plafond zijn altijd stabiel.
• Elke andere plank is stabiel als zowel zijn linker als rechter eindpunt zijn bevestigd aan een stabiele plank.

Let op! Deze definitie van stabiliteit komt niet geheel overeen met de werkelijkheid. In werkelijkheid is het soms mogelijk om een plank A aan een andere plank B op te hangen die zelf op plank A steunt. Wanneer zo'n constructie wel of niet stabiel is, is niet triviaal (je hebt wat natuurkunde nodig om dat uit te zoeken), in deze logische puzzel sluiten we zulke constructies daarom uit.

Functioneel

Elk onderdeel van de constructie moet functioneel zijn. Planken mogen alleen aan hun uiteindes worden ondersteund of opgehangen (niet in het midden), en elk uiteinde wordt óf met een ketting óf met een paal bevestigd (niet allebei). Er mogen nergens delen van palen of kettingen zijn die niet worden gebruikt om een plank mee te bevestigen.

 Pentomino's

(Aad van de Wetering en Odette De Meulemeester)

Hiernaast staan alle pentomino’s met hun naam.

Verdeel het raster hieronder in pentomino's zodat geen twee pentomino's met dezelfde vorm (ook niet gedraaid of gespiegeld) een zijde gemeen hebben. Een vierkantje met een letter erin moet deel uit maken van de pentomino met dezelfde naam.

 

Bekijk oplossing