
Pythagon prijsvraag
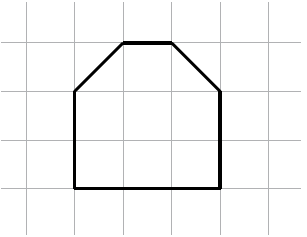
Een pythagon is een vierkant van 1 $\times$ 1 met twee keer daaraan vastgeplakt een gelijkbenige rechthoekige driehoek. In figuur 1 zie je een voorbeeld op ruitjespapier. In totaal bestaan er zeven verschillende pythagons (spiegelsymmetrische pythagons tellen beide mee); je ziet ze in figuur 2.
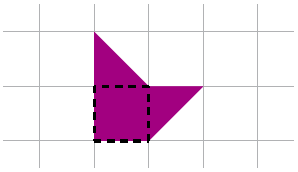
keer daaraan vastgeplakt een gelijkbenige rechthoekige driehoek

De zijden van een pythagon hebben allemaal als lengte 1, 2, √2 of 2√2. We noemen de waarde 1 de rechte eenheidslengte en √2 de diagonale eenheidslengte. We spreken over deze twee getallen kortweg als eenheidslengte (zie figuur 3).
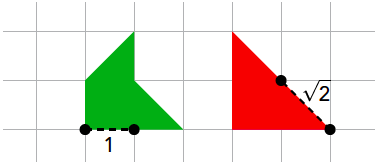
Met pythagons kan je heel veel figuren leggen. De spelregels zijn als volgt:
- Twee pythagons mogen tegen elkaar aangelegd worden, als ze met ten minste ..n eenheidslengte aan elkaar raken.
- Een rechte zijde mag alleen aan een rechte en een schuine alleen aan een schuine. Een zijde mag wel over een lengte van twee eenheden raken.
- Een pythagon behoudt zijn vorm en afmetingen; in het bijzonder mag een pythagon niet worden vergroot of verkleind.
- Een pythagon mag een ander niet overlappen.
In figuur 4 zie je twee mogelijkheden om de zeven pythagons neer te leggen. De oppervlaktes van deze vormen zijn natuurlijk gelijk: elk pythagon heeft oppervlakte 2, dus beide figuren hebben oppervlakte $7 \times 2 = 14$. De omtrekken zijn verschillend: de linkerfiguur heeft omtrek 12 + 6√2 en de omtrek van de rechterfiguur is 16 + 10√2 (buiten plus binnen).

Minimale en maximale omtrek met twee pythagons
Elk pythagon heeft 2 schuine en 4 rechte eenheidslengtes. Ze hebben dus allemaal dezelfde omtrek. Als we twee pythagons tegen elkaar aanleggen, kan de omtrek verschillend zijn. Hoe kunnen we steeds een zo klein mogelijke omtrek krijgen bij een gegeven oppervlakte en dus een gegeven aantal pythagons?
Bekijk de drie configuraties in figuur 5. De linker heeft omtrek 6 + 2√2, de middelste heeft omtrek 8 en de rechter 2 + 4√2. Van deze drie getallen is het laatste getal het kleinst; het is ook de kleinst mogelijke omtrek van .lle mogelijke samenstellingen van twee pythagons, want het is het enige geval waar drie eenheden aan elkaar raken.
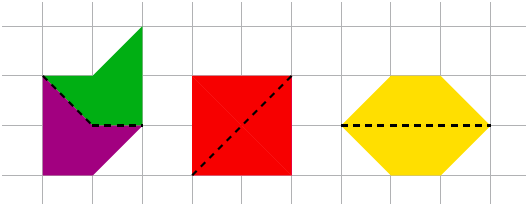
Kun je zelf aantonen dat 6 + 2√2 de grootste omtrek is die je met twee verschillende pythagons kan krijgen?
Verschillende pythagons
We kijken vanaf nu alleen maar naar combinaties van verschillende pythagons (de configuraties in het midden en rechts van figuur 5 doen dus niet mee). We gaan eerst proberen om rechthoeken te maken. We beginnen met drie pythagons, dus met oppervlakte 6.
Maak een rechthoek van 3 $\times$ 2, met drie verschillende pythagons. Dan één van 4 $\times$ 2, met vier verschillende pythagons. En tot slot één van 5 $\times$ 2, met vijf verschillende pythagons.
Deze rechthoeken hebben oppervlaktes 6, 8 en 10. De bijbehorende omtrekken zijn 10, 12 en 14. Er zijn echter nog andere rechthoeken met deze oppervlaktes. Omdat
$$6 = 6 \times 1 = 3√2 \times √2 = 3 \times 2$$
zijn er nog twee andere rechthoeken met oppervlakte 6. Net zo is
$$8 = 8 \times 1 = 4√2 \times √2 = 4 \times 2 = 2√2 \times 2√2$$
en
$$10 = 10 \times 1 = 5√2 \times √2 = 5 \times 2.$$
De rechthoeken zijn afgebeeld in figuur 6. Het blijkt dat geen van de rechthoeken, afgezien die van 3 $\times$ 2, 4 $\times$ 2 en 5 $\times$ 2, met verschillende pythagons gevuld kan worden.
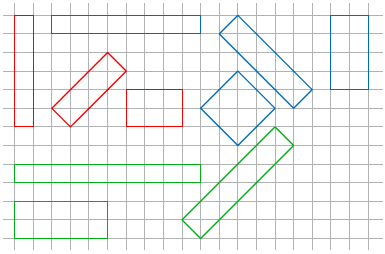
van oppervlakte 8 en groene rechthoeken van oppervlakte 10.
Het geval 3 $\times$ 2 is inderdaad de configuratie met de kleinste omtrek. Voor het geval van oppervlakte 8 is er nog een betere configuratie te verzinnen: zie figuur 7. Probeer deze figuur zelf eens met vier verschillende pythagons te vullen.
We zagen dat we met vijf verschillende pythagons in elk geval een rechthoek van 2 $\times$ 5 kunnen maken. Deze heeft een omtrek van 14. Andere rechthoeken lukken niet. Maar misschien wel andere figuren met een kleinere omtrek. In figuur 8 zie je nog eens vijf vormen met oppervlakte 10. De omtrekken zijn verschillend. Zie jij in welke vorm vijf verschillende pythagons passen?
Met zes verschillende pythagons hebben wij een vorm gevonden met een omtrek van 6 + 6√2 ≈ 14,5 en met zeven een vorm met een omtrek van 10 + 4√2 ≈ 15,7. Zijn deze waarden minimaal?
De prijsvraag
De vragen die we tot nu toe stelden, zijn bedoeld om je vertrouwd te maken met de pythagons; ze horen niet bij de opgaven van de prijsvraag. De prijsvraag is onderverdeeld in drie categorieën. De eerste categorie gaat over het vinden van een minimale omtrek bij een gegeven aantal pythagons. De tweede gaat over het omvatten van een zo groot mogelijk oppervlak door middel van een keten aaneengesloten pythagons en bij de derde staat een artistieke wiskundige prestatie centraal.
Op onze website (http://www.pyth.eu) staan alle pythagons, die je op gekleurd papier kan afdrukken en uitknippen.
A: Kleinste omtrek bij gegeven aantal
Maak van een gegeven aantal verschillende pythagons een vorm, zodanig dat de omtrek minimaal is. Tot en met vier pythagons hebben we het al gedaan. Als je voor vijf pythagons kunt bewijzen dat jouw manier de kleinste omtrek geeft, stuur je je configuratie op met een bewijs. Als je geen bewijs kunt vinden, stuur je alleen je configuratie. Vermeld er wel bij wat de omtrek ervan is!
Hetzelfde kun je doen met zes en zeven pythagons.
Voor een vorm die uit acht pythagons bestaat, neem je de volledige set van zeven verschillende pythagons, waaraan je naar keuze nog één pythagon toevoegt (één pythagon komt dus twee keer voor). Bij negen pythagons voeg je twee verschillende pythagons toe aan de volledige set, enzovoort. Als je bij vijftien bent aangekomen, neem je twee volledige sets, waaraan je nog één pythagon toevoegt.
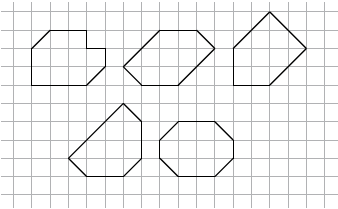
oppervlakte 10) zijn achtereenvolgens één keer
10 + 2√2 ≈ 12,8, daarna drie keer 4 + 6√2 ≈ 12,5
en ten slotte één keer 6 + 4√2 ≈ 11,7.
Het is de bedoeling dat je de tabel bovenaan de rechterkolom zo ver mogelijk aanvult. De middelste kolom is het moeilijkst: dit vergt echt een bewijs. De schattingen in de rechterkolom, vooral voor de waarden 8 en 9, kunnen natuurlijk veel beter.
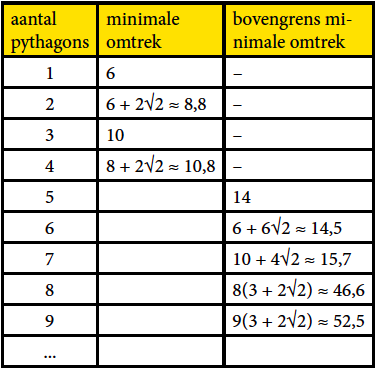
Als je exact weet wat de minimale omtrek is, is dat natuurlijk het beste en schrijf je je getal in de middelste kolom. Als je een vorm hebt die de kleinste omtrek geeft die jij kunt vinden, maar waarvan je niet kunt aantonen dat het echt de minimale omtrek is, dan heb je een bovengrens gevonden en zet je die in de rechterkolom.
Wiskundigen generaliseren graag: valt er iets te zeggen over de bovengrens bij $n$ pythagons? Een zeer ruime bovengrens is $n(3 + √2)$. Als jij een betere schatting kunt maken van zo’n bovengrens (uitgedrukt in $n$), horen we dat natuurlijk graag! De jury beoordeelt de bovengrens zelf, maar ook de kwaliteit van je redenering.
B: Grootste oppervlakte omsingeld
Wat is het grootste gebied dat je met een vast aantal pythagons kan omsingelen? De pythagons die raken, moeten dit doen over een of twee eenheidslengtes: alleen raken door middel van een punt is niet voldoende. In de linkerconfiguratie van figuur 9 wordt een oppervlakte op een toegestane manier omsingeld door zes pythagons. In de rechterconfiguratie beschouwen we de witte oppervlakte in het midden als niet omsingeld.
Probeer het eerst met drie pythagons, dan met vier en zo verder tot en met zeven. Met acht pythagons kies je naar keuze nog één pythagon, naast de volledige set van zeven. Bij negen pythagons mag je naast de volledige set nog twee verschillende andere kiezen, enzovoort.

rechts: een niet toegestane manier
C: Structuren en patronen
Pythagons zijn moeilijk combineerbare objecten. Toch kun je er mooie dingen mee doen: met paarse en groene pythagons kun je bijvoorbeeld een hele muur behangen, zoals je in figuur 10 ziet. Fraaie vormen, vlakvullingen, noem maar op. Als je wat moois bedenkt, kun je je creatie naar ons opsturen.

Nieuwjaarsopdracht
Ook dit jaar hebben we weer een nieuwjaarsopdracht, waaraan je tot 1 januari 2017 kunt meedoen:
- Wat is de kleinste omtrek die je met 217 pythagons kan maken? Gebruik precies 31 keer de gehele verzameling van zeven pythagons (7 $\times$ 31 = 217).
- Wat is het kleinste aantal pythagons waarmee je een oppervlakte van 217 kan omcirkelen? De aantallen van verschillende soorten pythagons mogen onderling maar 1 verschillen. (Dus je gebruikt bijvoorbeeld vijf pythagons 87 keer en twee pythagons 88 keer.)
- Schrijf op de mooiste manier het getal 2017, met 217 of meer pythagons. Je mag best het ene pythagon meer gebruiken dan het andere.
Inzenden
Iedereen kan aan de pythagonprijsvraag meedoen: leerlingen, beroepswiskundigen, hobbyïsten, enzovoorts. Ook als klas kun je inzenden. In elke categorie is er een prijs van € 50. Bovendien zijn er nog enkele kleinere prijzen. De jury behoudt zich het recht voor om niet alle prijzen uit te reiken, of om het prijzengeld te verdelen onder meerdere inzenders. Inzenden kan alleen digitaal, het liefst als pdf. Je mag ook een foto van je creatie maken en deze digitaal inzenden.
Mail je inzending naar [email protected]. Vermeld duidelijk de naam van de categorie: A, B, C of de nieuwjaarsopdracht. Je mag in meerdere categorieën inzenden en uiteraard zijn we ook in deelresultaten geïnteresseerd.
Vermeld verder je naam en adres, en als je scholier bent, de naam en het adres van de school, je leeftijd en je klas. Bij een klasseninzending moet bovendien de naam van de wiskundedocent opgegeven worden.
Inzendingen moeten bij ons binnen zijn vóór 10 april 2017.
