Een pythagon is een vierkant van 1 × 1 met twee keer daaraan vastgeplakt een gelijkbenige rechthoekige driehoek. Er bestaan zeven verschillende pythagons (pythagons die elkaars spiegelbeeld zijn tellen beide mee); je ziet ze in de bovenstaande figuur. Over deze vormen ging de prijsvraag van dit jaar.

Er waren drie opdrachten:

A. Maak van een gegeven aantal verschillende pythagons een vorm, zodanig dat de omtrek minimaal is.

B. Wat is het grootste gebied dat je met een vast aantal pythagons kan omsingelen?

C. Verzin, uiteraard gebruikmakend van pythagons, fraaie vormen, vlakvullingen, noem maar op.

Het prijzengeld wordt verdeeld onder Aad van de Wetering en Helmut Postl.

Opdracht A

Aad van de Wetering doet een interessante observatie. De driehoekjes die uitsteken, zijn heel vervelend aan elkaar te passen. Aad introduceert het begrip halfwaarde. Aan elk driehoekje kent hij een waarde toe:

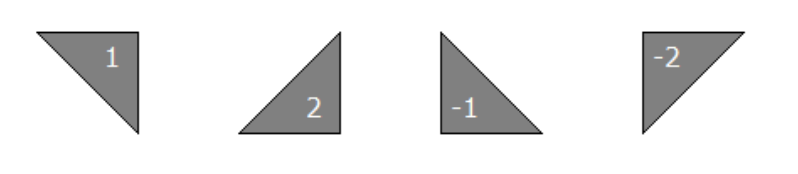
Vervolgens berekent hij voor de zeven pythagons de som van de halfwaarden. De roze, lichtblauwe en donderblauwe pythagon hebben altijd halfwaarde 0. De paarse, groene en gele pythagon hebben halfwaarde –3, –1, 1 of 3, afhankelijk van de rotatie. Ten slotte heeft de rode pythagon halfwaarde –4, –2, 2 of 4, afhankelijk van de rotatie. Tenslotte heeft de rode pythagon halfwaarde –4, –2, 4 of 4, afhankelijk van de rotatie.

Er geldt dat als driehoekjes tegen elkaar kunnen worden gelegd, de som van de halfwaarden nul is. Zodoende kan Aad direct concluderen dat het met een oneven aantal sets pythagons onmogelijk is om een rechthoek te leggen, vanwege het feit dat de som van de halfwaarden niet nul is.

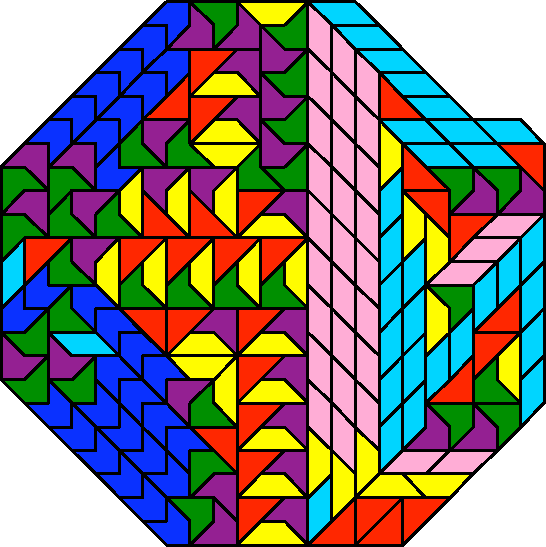
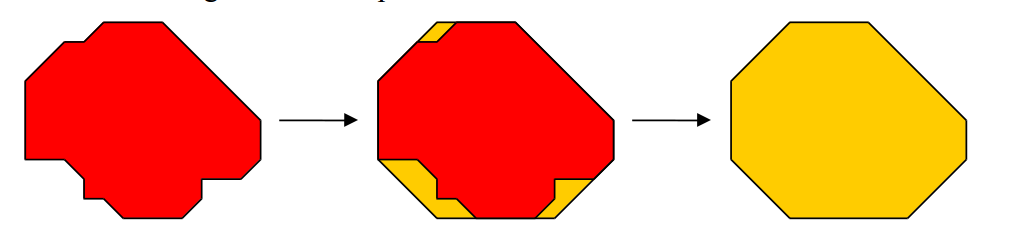
Om een aantal pythagons zó neer te leggen dat de omtrek minimaal is, valt niet mee. De meeste inzenders kwamen uit op een vorm die wat weg heeft van een cirkel, zoals figuur 1. Het klopt dat van even grote oppervlakken, het oppervlak dat cirkelvormig is de kleinste omtrek heeft. Maar in het geval van pythagons gaat het niet op. Het blijkt dat de achthoek (zie figuur2) de kleinste omtrek heeft. Edo Timmermans en Helmut Postl kwamen beide tot deze conclusie. Helmut Postl geeft echter ook een bewijs dat als de pythagons in de vorm van een achthoek worden gelegd, de omtrek minimaal is (zie figuur 3).

Tot slot is hier een tabel waarin je voor de aantallen pythagons tot en met 21 kunt zien wat de minimale omtrek is.

aantal pythagons	minimale omtrek
2	6+2√2 $\approx$ 8,8
3	4+4√2 $\approx$ 9,7
4	8+2√2 $\approx$ 10,8
5	4+6√2 $\approx$ 12,5
6	8+4√2 $\approx$ 13,7
7	12+2√2 $\approx$ 14,8
8	10+4√2 $\approx$ 15,7
9	10+4√2 $\approx$ 15,7
10	8+6√2 $\approx$ 16,5
11	6+8√2 $\approx$ 17,3
12	10+6√2 $\approx$ 18,5
13	8+8√2 $\approx$ 19,3
14	14+4√2 $\approx$ 19,7
15	12+6√2 $\approx$ 20,5
16	10+8√2 $\approx$ 21,3
17	10+8√2 $\approx$ 21,3
18	8+10√2 $\approx$ 22,1
19	6+12√2 $\approx$ 23,0
20	18+4√2 $\approx$ 23,7
21	16+6√2 $\approx$ 24,5

Opdracht B

De grootste oppervlakte met pythagons omsingelen is iets heel anders. Slechts twee inzenders werkten dit probleem uit, namelijk Edo Timmermans en Aad van de Wetering. Zij tekenden voor kleine aantallen pythagons hun oplossingen. De ingesloten oppervlakken waren min of meer gelijk. In figuur 4 zie je Aads oplossing voor de aantallen pythagons 4 tot en met 13, en tot en met 21 pythagons staan de waarden van de maximale ingesloten oppervlakte in onderstaande tabel. Aads oplossing was in het geval van zes pythagons net iets beter dan die van Edo.

aantal pythagons	maximale ingesloten oppervlakte
4	1
5	3
6	6
7	8
8	11,5
9	17
10	23,5
11	27
12	33
13	37
14	43
15	51
16	57,5
17	67,5
18	74,5
19	82
20	89,5
21	101,5

Wat opvalt bij de oplossing van Aad, is dat de pythagons opnieuw een achthoek omschrijven. Helaas geeft hij er geen bewijs van, maar wellicht is er een bewijs te vinden dat zo het grootste oppervlak kan worden ingesloten.

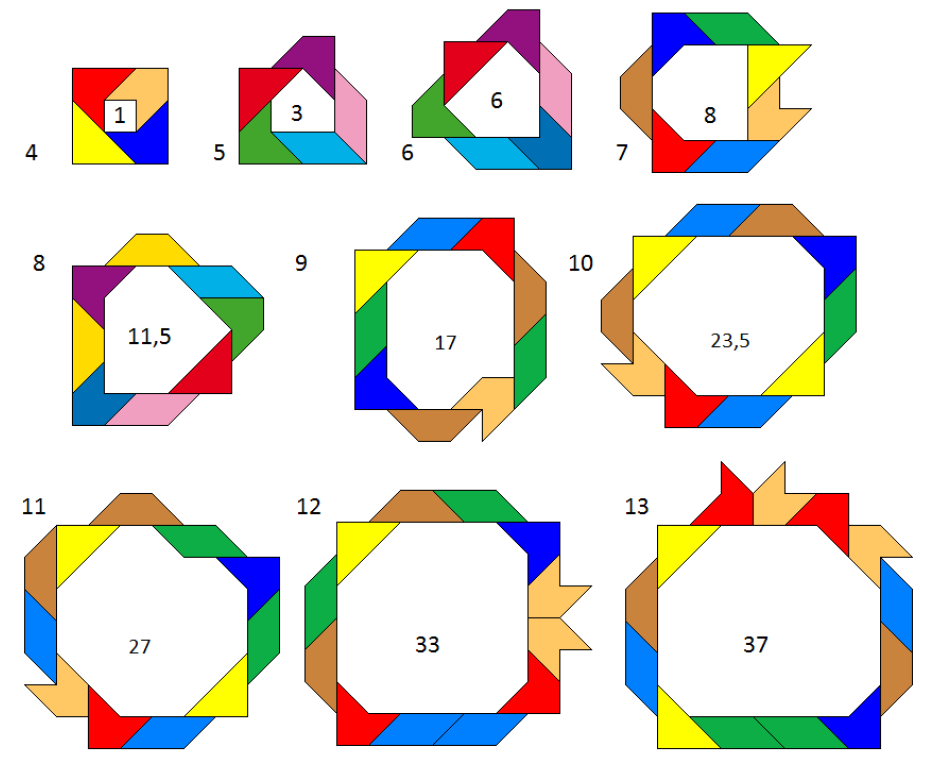
Opdracht C

 

Wat betreft fraaie vormen, structuren en vlakvullingen: hier konden ook de jongste deelnemers zich uitleven. Vooral de vindingen van, opnieuw, Aad van de Wetering, zijn heel bijzonder. We laten hier een behangpapier zien, bestaande uit het klavertje-vier-patroon dat je in figuur 5 ziet. Als de inhammen opgevuld worden met rode pythagons, ontstaat het behang in figuur 6.

 

Ook figuur 7 is van Aad Je ziet daar een `geomagisch vierkant' met in elke rij, kolom en diagonaal vier pythagons (lichtblauw, paars, geel en rood). Met die vier vormen kun je alle zeven pythagons (met een vier keer zo grote oppervlakte) maken. In twee gevallen moesten pythagons helaas gespiegeld worden.