Opgave 342 [niveau oOO]

Laat zien dat het getal $2 \cdot 7^n + 4 · 5^{2n} + 3$ deelbaar is door $9$ voor elk natuurlijk getal $n$.

 

Opgave 343 [niveau oOO]

In een museum kun je in de garderobe je jas afgeven. Er wordt een bonnetje met nummer bevestigd aan de jas, en eenzelfde bonnetje met nummer ontvang je. Na afloop van het bezoek kun je met dit bonnetje je jas weer ophalen. Het personeel dat in de garderobe werkt, maakte onlangs fouten met het onjuist lezen (op de kop lezen) van bonnetjes. Hierop besloot de directie alle nummers die op twee manieren te lezen zijn te verwijderen (bijvoorbeeld 861 en 198). Hoeveel getallen, tussen 000 en 999, zijn wél bruikbaar? Misverstanden ontstaan bij de cijfers 0, 1, 6, 8 en 9.

 

Opgave 344 [niveau ooO]

Hiernaast zie je een taartje voorzien van bananen- en frambozencrème. Eric en Suzan willen dit taartje delen, zó dat beiden evenveel taart krijgen met bananen- en frambozencrème. Hoe kun je de taart met één snede eerlijk in twee delen? De rand tussen de bananen- en frambozencrème bestaat uit twee identieke halve cirkels.

 

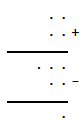Opgave 345 [niveau ooO]

In de volgende optelsom komen alle cijfers van 0 tot en met 9 voor. Een getal begint uiteraard niet met een 0. Helaas zijn alle cijfers verdwenen. Bepaal het aantal mogelijke oplossingen.

 

 

Bekijk oplossing