Oplossing 342 [niveau oOO]

Laat zien dat het getal $2 \cdot 7^n + 4 · 5^{2n} + 3$ deelbaar is door $9$ voor elk natuurlijk getal $n$.
Oplossing. We maken gebruik van het feit dat $25^n$ altijd te schrijven is als $7^n$ plus een negenvoud. Dit is een specifiek geval van de zogeheten ‘negenproef ’, die al vaker in dit blad is besproken, onder andere in het artikel ‘Slim vermenigvuldigen’, Pythagoras 53-1 (september 2013).
Er geldt: $5^{2n} = 25^n = (7 + 18)^n = 7^n$ plus een negenvoud. Zodoende is $2 · 7^n + 4 · 5^{2n} + 3 = 2 · 7^n + 4 · 7^n + 3 + \text{ negenvoud } = 6 · 7^n + 3 + \text{ negenvoud}$. Nu geldt dat $6 · 7^n$ altijd een negenvoud plus $6$ is. Dit kun je eenvoudig inzien met de negenproef. Uiteindelijk volgt dat $2 · 7^n + 4 · 5^{2n} + 3 = 6 · 7^n + 3 + \text{ negenvoud } = \text{ negenvoud } + 9 = \text{ negenvoud}$.
De opgave is overigens ook met behulp van volledige inductie op te lossen, een bewijsprincipe dat in de bovenbouw bij Wiskunde D aan de orde komt.

 

Oplossing 343 [niveau oOO]

In een museum kun je in de garderobe je jas afgeven. Er wordt een bonnetje met nummer bevestigd aan de jas, en eenzelfde bonnetje met nummer ontvang je. Na afloop van het bezoek kun je met dit bonnetje je jas weer ophalen. Het personeel dat in de garderobe werkt, maakte onlangs fouten met het onjuist lezen (op de kop lezen) van bonnetjes. Hierop besloot de directie alle nummers die op twee manieren te lezen zijn te verwijderen (bijvoorbeeld 861 en 198). Hoeveel getallen, tussen 000 en 999, zijn wél bruikbaar? Misverstanden ontstaan bij de cijfers 0, 1, 6, 8 en 9.
Oplossing. Het is duidelijk dat als een nummer minstens één van de getallen 2, 3, 4, 5, 7 bevat, het bonnetje eenduidig is. Eventueel onduidelijke bonnetjes bevatten alléén cijfers uit de verzameling {0, 1, 6, 8, 9}. Dat zijn in het totaal 5³ = 125 getallen. Een aantal van de getallen die je met deze cijfers kunt vormen leiden niet tot problemen, namelijk als de bon na een draaiing van 180 graden hetzelfde getal aangeeft. Daarvoor moet in het midden een 0, 1 of 8 staan. Op de eerste plaats kunnen alle vijf cijfers voorkomen. Steeds is dan het laatste cijfer uniek bepaald (want dat moet identiek zijn aan het eerste cijfer). Het gaat om 15 getallen, namelijk 000, 010, 080, 101, 111, 181, 609, 619, 689, 808, 818, 888, 906, 916 en 986. Het aantal te gebruiken getallen is dus 10³ – 5³ + 15 = 890.

 

Oplossing 344 [niveau ooO]

Hiernaast zie je een taartje voorzien van bananen- en frambozencrème. Eric en Suzan willen dit taartje delen, zó dat beiden evenveel taart krijgen met bananen- en frambozencrème. Hoe kun je de taart met één snede eerlijk in twee delen? De rand tussen de bananen- en frambozencrème bestaat uit twee identieke halve cirkels.
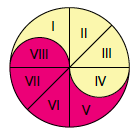
Oplossing. Neem aan dat de straal van het cirkelvormige taartje gelijk is aan 1. Teken drie lijnen door het middelpunt: één verticaal, één horizontaal en één diagonaal, zoals in de figuur rechts. De cirkel wordt zo in acht stukken verdeeld. Die stukken zijn allemaal even groot. Voor de delen II, III, VI en VII is dat direct duidelijk (die hebben elk oppervlakte ${1 \over 8}\pi$). De delen IV en VIII hebben elk een oppervlakte van ${1 \over 2} · \pi ({1 \over 2})^2 = {1 \over 8}\pi$. Voor de delen I en V blijft dan ook elk ${1 \over 8}\pi$ over. De gezochte snijlijn is dus de diagonale lijn.

 

Oplossing 345 [niveau ooO]

In de volgende optelsom komen alle cijfers van 0 tot en met 9 voor. Een getal begint uiteraard niet met een 0. Helaas zijn alle cijfers verdwenen. Bepaal het aantal mogelijke oplossingen.

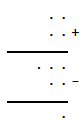
Oplossing. We vullen variabelen $a, b, ..., j$ in:

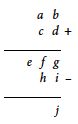
Met $ab$, $cd$, $efg$, $hi$ en $j$ geven we de verschillende getallen weer. We hebben de volgende observaties:

• $ab, cd < 100$, dus $efg < 200$, dus $e = 1$.
• $j < 10$ en $efg > 100$, dus $hi > 90$, dus $h = 9$.
• $hi < 100$ en $j < 10$, dus $efg < 110$, dus $f = 0$.
• $a + c = 9$ of $a + c = 10$.
• $i + j = g + 10$ en $b + d = g$ of $b + d = g + 10$.

We maken een tabel met de resterende cijfers $2, 3, 4, 5, 6, 7$ en $8$, waarbij we er van uitgaan dat $a < c, b < d$ en $i < j$:

In de tabel staat een X als er geen getal meer is waarmee de berekeningen kloppend gemaakt kunnen worden. Uiteindelijk moeten we het aantal oplossingen tellen. De tabel bevat drie geldige oplossingen. Voor elke regel met een oplossing die we vinden, geldt dat $a$ en $c$, $b$ en $d$, en $i$ en $j$ kunnen worden verwisseld. Daarmee komt het totale aantal oplossingen op $3 \times 2^3 = 3 \times 8 = 24$.