Opgave 354 [niveau oOO]

Hieronder zie je een cirkel met twee lijnstukken die loodrecht op elkaar staan. Wat is de straal van de cirkel?

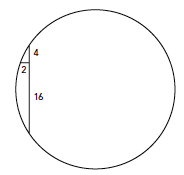
Opgave 355 [niveau oOO]

Hoe vaak per dag staan de grote en kleine wijzer van een klok precies loodrecht op elkaar?

 

Opgave 356 [niveau ooO]

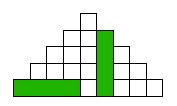Een $n$-piramide is een piramide zoals in de figuur rechts. De piramide bestaat uit $n$ rijen witte blokjes (in de figuur is $n = 5$, maar deze opgave gaat over algemene $n$). De bovenste rij heeft $1$ blokje, de tweede rij $3$ blokjes, de derde rij $5$ blokjes, ..., de $n$-de rij $2n – 1$ blokjes. Het middelste blokje van elke rij ligt steeds precies onder het blokje in de bovenste rij. We leggen een aantal groene rechthoeken van vier naastgelegen blokjes neer. Die rechthoeken moeten allemaal helemaal in de piramide liggen en verschillende rechthoeken mogen elkaar niet overlappen. In de figuur zijn twee van zulke rechthoeken getekend. Wat is het kleinst mogelijke aantal blokjes van een $n$-piramide dat niet door een groene rechthoek wordt overdekt?

 

Opgave 357 [niveau ooO]

Op een eiland leven drie soorten mensen: mensen die uitsluitend de waarheid spreken, mensen die soms de waarheid spreken en soms liegen, en mensen die uitsluitend liegen. Mensen die tot dezelfde soort behoren, dragen allemaal eenzelfde kleur pet. Er zijn gele, rode en blauwe petten. Een toerist die het eiland bezoekt, is niet op de hoogte welke kleur bij welke groep hoort. De toerist ziet drie mannen met verschillend gekleurde petten. De man met de rode pet zegt tegen de toerist: ‘Ik lieg vaker dan iemand met een gele pet.’ Daarna zegt de man met de blauwe pet: ‘De man met de rode pet heeft zojuist gelogen.’ Tot slot zegt de man met de gele pet: ‘Precies een van de twee mannen met de rode en blauwe pet heeft zojuist gelogen.’ Kan de toerist nu bepalen bij welke soorten mensen de petkleuren horen?

Bekijk oplossing