Pythagoras Olympiade 57-1, september 2017
Opgave 362 [niveau oOO]
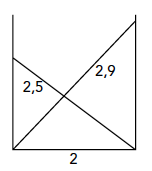
In een steeg van 2 meter breed worden twee ladders van 2,5 en 2,9 meter zoals in onderstaande figuur tegen de twee tegenoverstaande gevels geplaatst. Op welke hoogte kruisen de ladders elkaar?
Opgave 363 [niveau oOO]
Gegeven zijn twee verzamelingen: $A = \{1, 2, 3, ..., 20\}$ en $B = \{21, 22, 23, ..., 30\}$. Arthur berekent het product van elk tweetal getallen waarbij één getal uit $A$ komt en één getal uit $B$. Aan het eind telt hij alle producten op. Wat is de uitkomst van die som?
Opgave 364 [niveau ooO]
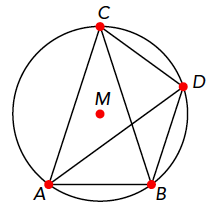
Gegeven is een gelijkbenige driehoek $ABC$ met $|AC| = |BC|$. De lijn door $B$ evenwijdig met $AC$ en de omgeschreven cirkel van driehoek $ABC$ snijden elkaar in punt $D$. Ten slotte geldt dat $\angle BAD = \angle ACB$. Bereken $\angle ACB$.
Opgave 365 [niveau ooO]
De getallen $1,1+ {1 \over 2},1+ {1 \over 2} + {1 \over 3} ,1+ {1 \over 2} + {1 \over 3} + {1 \over 4},...$ zijn harmonische getallen. Druk de som
$$J(n) = {1 \over n}+{2 \over n-1}+{3 \over n-2}+...+{n-1 \over 2}+{n \over 1}$$
uit in een expressie waar het $n$-de harmonische getal
$$H(n)=1+{1 \over 2}+{1 \over 3}+{1 \over 4}+...+{1 \over n-1}+{1 \over n}$$ precies één keer in voorkomt.
