Oplossing 362 [niveau oOO]

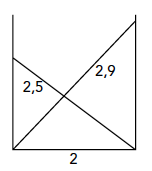In een steeg van 2 meter breed worden twee ladders van 2,5 en 2,9 meter, zoals in de figuur links, tegen de twee tegenoverstaande gevels geplaatst. Op welke hoogte kruisen de ladders elkaar?
Oplossing. Noem de uiteindes van de ladders $A$, $B$, $C$ en $D$ en hun snijpunt $S$. Het punt op $BC$ recht onder $S$ noemen we $T$. Tenslotte zetten we $|ST|$ gelijk aan $x$ en $|BT|$ gelijk aan $y$. Uit de stelling van Pythagoras volgt dat $|AB| = 1,5$ en $|CD| = 2,1$. Doordat de driehoeken $BCD$ en $BTS$ tezamen een snavelfiguur vormen, zien we dat ze gelijkvormig zijn. In het bijzonder 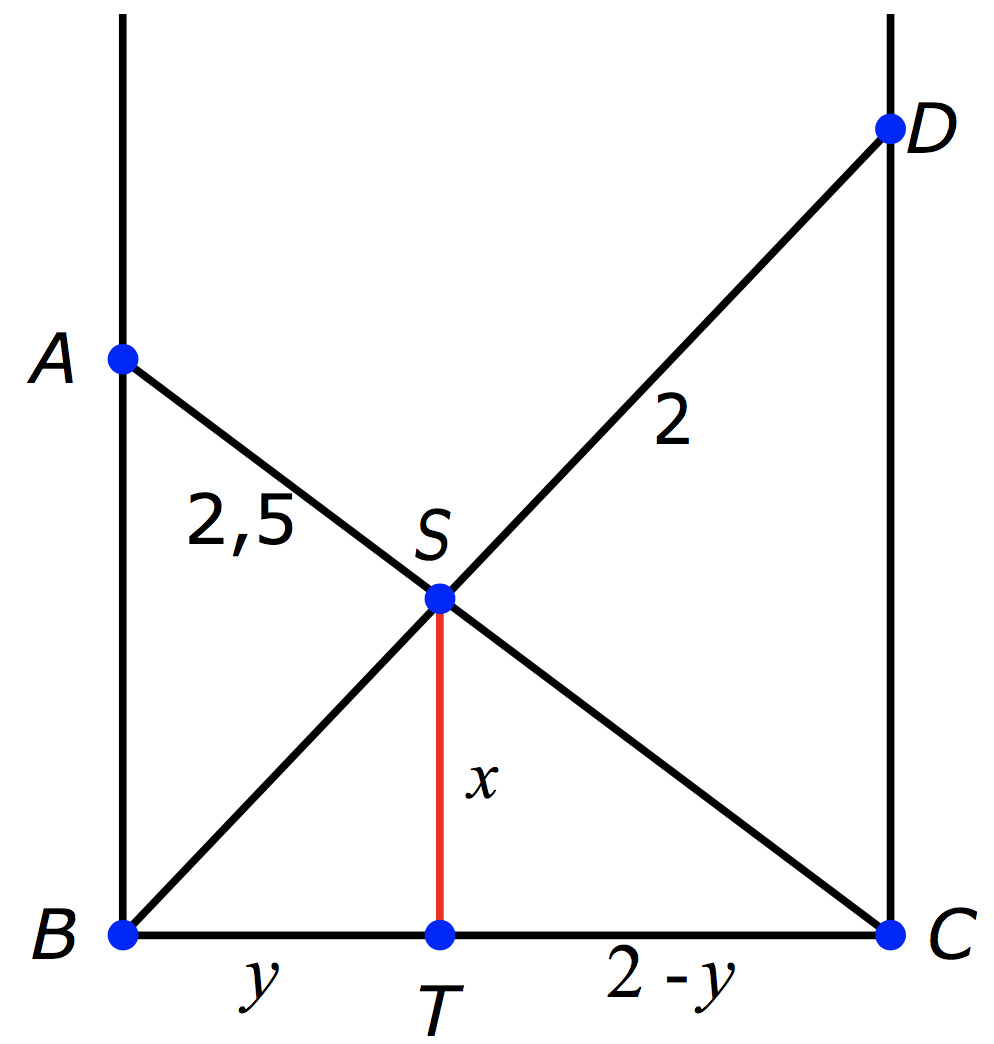geldt dus dat ${y \over x} ={|BC| \over|CD|} = {2 \over 2,1}$. Met andere woorden, we vinden dat $y$ gelijk is aan ${2x \over 2,1}$ . Evenzo vormen $CBA$ en $CTS$ een snavelfiguur, waardoor dus geldt dat ${|ST| \over |CT|} = {|AB| \over |BC|} = {1,5 \over 2}$. Vullen we $|ST| = x$ en $|CT| = 2 - y$ in, dan vinden we ${x \over 2-y} = {1,5 \over 2}$ . Samen met onze eerdere uitdrukking voor $y$ geeft dit de vergelijking $x = (2-{2x \over 2,1}).{1,5 \over 2}$, wat oplost tot $x = {7 \over 8} = 0,875$. De gevraagde hoogte is dus $0,875$ meter.

 

Oplossing 363 [niveau oOO]

Gegeven zijn twee verzamelingen: $A = \{1, 2, 3, ..., 20\}$ en $B = \{21, 22, 23, ..., 30\}$. Arthur berekent het product van elk tweetal getallen waarbij één getal uit $A$ komt en één getal uit $B$. Aan het eind telt hij alle producten op. Wat is de uitkomst van die som? 
Oplossing. Laten we eerst de som van de producten uitschrijven wanneer we uit $A$ steeds de $1$ kiezen. Dit is $1 \times 21 + 1 \times 22 + ... + 1 \times 30 = 1 \times (21 + 22 + ... + 30)$. We vinden dus precies de som van de getallen uit $B$. Kiezen we uit $A$ steeds de $2$, dan vinden we $2 \times (21 + 22 + ... + 30)$, wat precies $2$ maal de som van de getallen uit $B$ is. Gaan we zo door en tellen we de resultaten bij elkaar op, dan vinden we als totale som precies de som van de getallen uit $A$ maal de som van de getallen uit $B$. Met de somformule van Gauss vinden we dat de som van de getallen uit $A$ gelijk is aan $(1 + 20) \times 10 = 210$ en die van uit $B$ gelijk is aan $(21 + 30) \times 5 = 255$. De uitkomst van de som is dus $210 \times 255 = 53550$.

 

Oplossing 364 [niveau ooO]

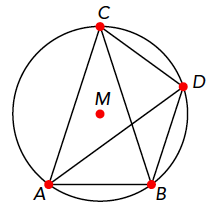Gegeven is een gelijkbenige driehoek $ABC$ met $|AC| = |BC|$. De lijn door $B$ evenwijdig aan $AC$ en de omgeschreven cirkel van driehoek $ABC$ snijden elkaar in punt $D$. Ten slotte geldt dat $\angle BAD = \angle ACB$. Bereken $\angle ACB$. 
Oplossing. We zetten hoek $ACB$ gelijk aan $\alpha$, wat dus ook gelijk is aan hoek $BAD$. Doordat de punten $C$ en $D$ op een boog aan dezelfde kant van lijnstuk $AB$ liggen, vinden we dat hoek $ADB$ ook gelijk is aan $\alpha$. Vervolgens merken we op dat de hoeken $ADB$ en $CAD$ gelijke $Z$-hoeken vormen, waardoor hoek $CAD$ dus eveneens gelijk is aan $\alpha$. 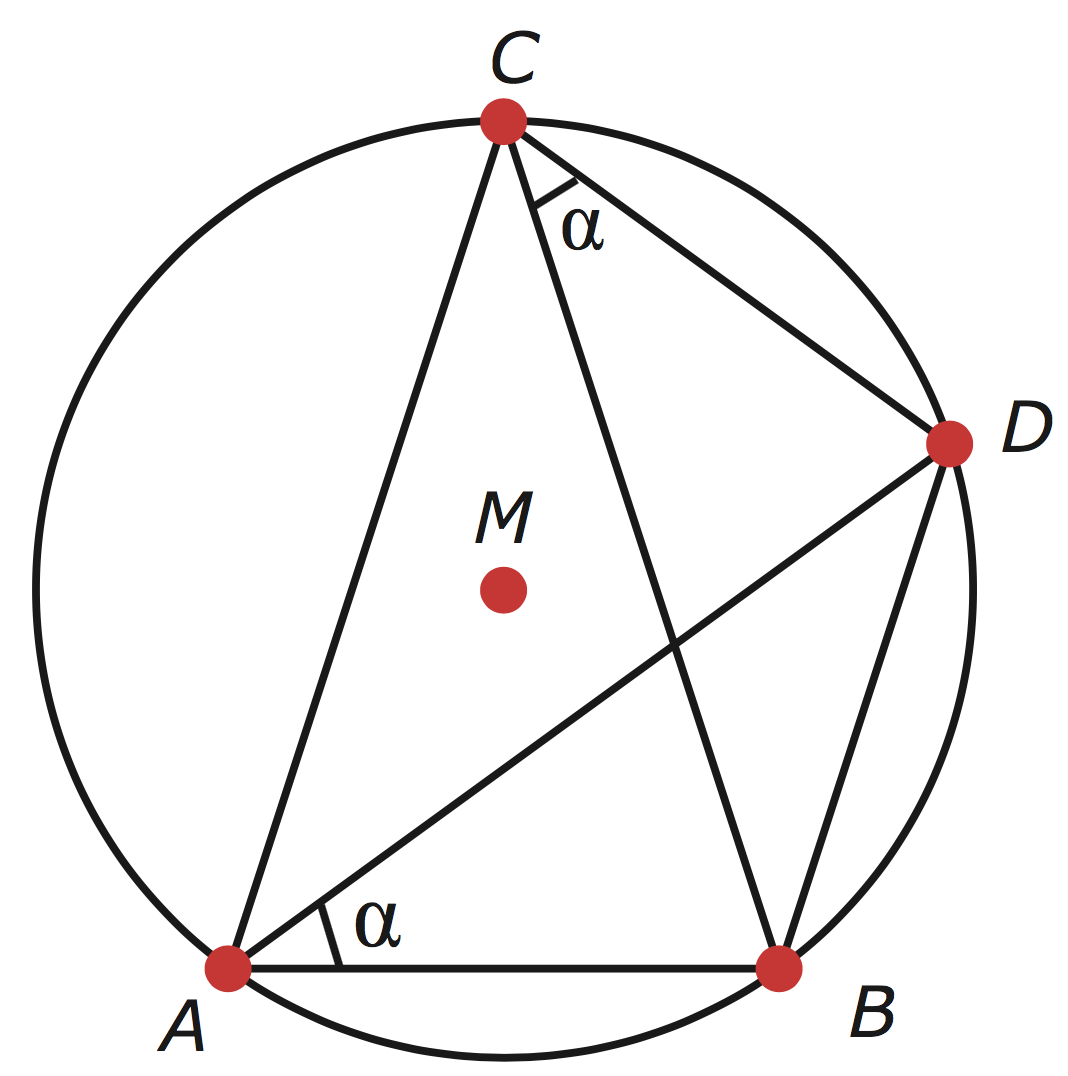Wat volgt is dat hoek $BAC$ gelijk is aan $BAD + CAD = 2 \alpha$. Hetzelfde geldt voor hoek $ABC$, aangezien driehoek $ABC$ gelijkbenig is. We vinden dus dat de totale som van de hoeken in driehoek $ABC$ gelijk is aan $\alpha$ + 2$\alpha$ +2$\alpha$ = 5$\alpha$. Aangezien deze waarde ook gelijk moet zijn aan $180$ graden, vinden we dat $\alpha = {180 \over 5} = 36^o$. Hoek $ACB$ is dus $36^o$.

 

Oplossing 365 [niveau ooO]

De getallen $1,1+ {1 \over 2},1+ {1 \over 2} + {1 \over 3} ,1+ {1 \over 2} + {1 \over 3} + {1 \over 4},...$ zijn harmonische getallen. Druk de som
$$J(n) = {1 \over n}+{2 \over n-1}+{3 \over n-2}+...+{n-1 \over 2}+{n \over 1}$$
uit in een expressie waar het $n$-de harmonische getal
$$H(n)=1+{1 \over 2}+{1 \over 3}+{1 \over 4}+...+{1 \over n-1}+{1 \over n}$$ precies één keer in voorkomt. 
Oplossing. We beweren dat $J(n)$ gelijk is aan $(n + 1)H(n) – n$. Om in te zien waarom dit zo is, schrijven we $n + 1$ maal de getallen ${1 \over 1}$ tot ${1 \over n}$ in een rechthoek. De totale som van deze getallen is dus $(n + 1)$ maal $H(n)$. Vervolgens tekenen we een zigzaglijn door de rechthoek, zodat in de eerste kolom alleen het bovenste getal boven de lijn ligt, in de tweede kolom alleen de bovenste twee getallen boven de lijn liggen, enzovoorts. De som van alle  getallen onder de zigzaglijn is dus gelijk aan ${n \over 1} + {n-1 \over 2} +... + {2 \over n-1} + {1 \over n} = J (n)$ . De som van de getallen boven de zigzaglijn is steeds per kolom gelijk aan $1$ en bedraagt dus $n$. Samen geeft dit $J(n) + n = (n + 1)H(n)$ en dus $J(n) = (n + 1)H(n) – n$.