Opgave 366 [niveau oOO]

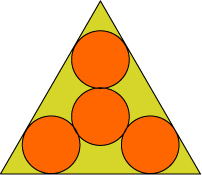
Vier cirkels met gelijke straal raken elkaar en de zijden van een gelijkzijdige driehoek met zijde 4 (zie plaatje). Bepaal de straal.

Opgave 367 [niveau oOO]

Piet wil graag een getal hebben waar je 2017 bij op kunt tellen om dan vervolgens hetzelfde getal terug te krijgen, maar dan met de cijfers in een andere volgorde. Is dit mogelijk? Waarom wel of niet?

Opgave 368 [niveau ooO]

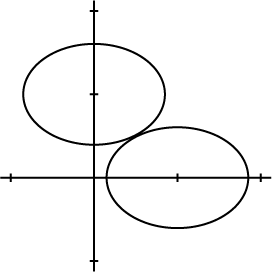
Hieronder zijn twee ellipsen getekend van de vorm $a(x-x_0)^2 + b(y - y_0)^2=1$, $(a, b > 0)$, waarbij $(x_0, y_0)$ respectievelijk $(1,0)$ en $(0,1)$ is. Aan welke voorwaarden moeten $a$ en $b$ voldoen om de ellipsen aan elkaar te laten raken?

Opgave 369 [niveau ooO]

Hoeveel getallen van 10 cijfers bestaan er met precies vier nullen, drie enen, twee tweeën en één drie? (Deze getallen beginnen niet met een nul.)

Bekijk oplossing