Oplossing 366 [niveau oOO]

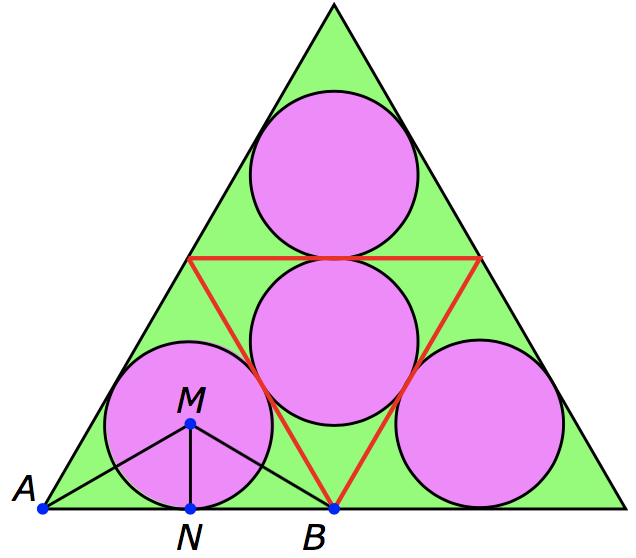Vier cirkels met gelijke straal raken elkaar en de zijden van een gelijkzijdige driehoek met zijde $4$ (zie plaatje). Bepaal de straal.

Oplossing. Verdeel de gelijkzijdige driehoek d.m.v. de drie rode lijnen in vier identieke gelijkzijdige driehoeken met zijde $2$. Het probleem is nu eenvoudig vertaald als volgt. Gegeven een gelijkzijdige driehoek met zijde $2$. Bepaal de straal van de ingeschreven cirkel.
Beschouw de punten $A$ (hoekpunt van de driehoek), $B$ (snijpunt van de oorspronkelijke driehoek en de rode lijnen), $M$ (middelpunt van de ingeschreven driehoek) en $N$ (punt precies in het midden van $AB$).
Er geldt $|AN| = 1$, $\angle NAM = 30^o$, $\angle ANM = 90^o$ en $\angle ANM = 60^o$. De straal die we zoeken is nu gelijk aan $|MN|$. Met behulp van speciale rechthoekige driehoeken is nu $|MN|$ uit te rekenen. $|AM| = {2 \over 3}\sqrt 3$ en $|MN| =  {1 \over 3}\sqrt 3$, de gevraagde straal.

Opgave 367 [niveau oOO]

Piet wil graag een getal hebben waar je 2017 bij op kunt tellen om dan vervolgens hetzelfde getal terug te krijgen, maar dan met de cijfers in een andere volgorde. Is dit mogelijk? Waarom wel of niet?

Oplossing. We beginnen heel simpel met een getal bestaande uit een cijfer $k$ en voor de rest nullen. Ofwel $N = k \cdot 10^n$. Als we het aantal nullen vergroten of verkleinen zodat $M = k ⋅ 10^m$, dan geldt voor het verschil $N –M = k ⋅ (10^n – 10^m)$. $10^n – 10^m$ is altijd deelbaar door $9$. Als $n > m$ dan is $10^n – 10^m$ een getal bestaande uit $n – m$ negens gevolgd door $m$ nullen, inderdaad deelbaar door $9$. Als we zoals in de opgave naar twee getallen kijken waarvan de cijfers zijn verwisseld dan is het verschil van deze twee getallen een negenvoud. Echter 2017 is geen negenvoud. Daarom kan Piet een dergelijk getal niet vinden.

Opgave 368 [niveau ooO]

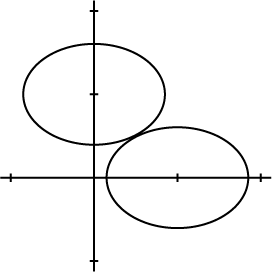Links zijn twee ellipsen getekend van de vorm $a(x-x_0)^2 + b(y - y_0)^2=1$, $(a, b > 0)$, waarbij $(x_0, y_0)$ respectievelijk $(1,0)$ en $(0,1)$ is. Aan welke voorwaarden moeten $a$ en $b$ voldoen om de ellipsen aan elkaar te laten raken?

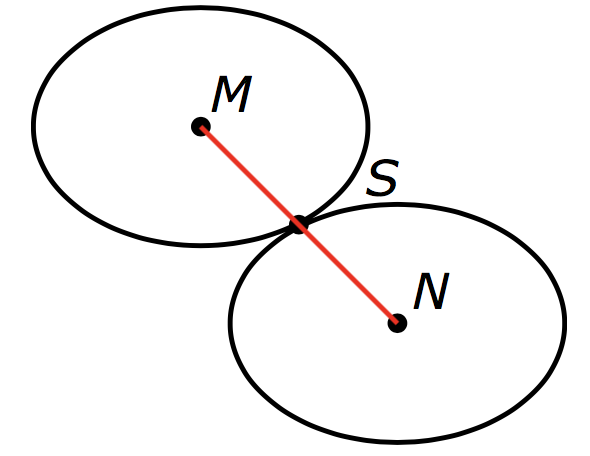
Oplossing. Met $M$ geven we $(0,1)$ weer en met $N$ geven we $(1,0)$ weer. De figuur van de twee ellipsen met middelpunten $M$ en $N$ is puntsymmetrisch met draaipunt \(S = ({1 \over 2},{1 \over 2})\). Dan moet $S$ het raakpunt zijn van de twee ellipsen. Dat betekent zeker dat $S$ op de ellipsen moet liggen, ofwel $a({1 \over 2})^2+b({1 \over 2})^2=1$. Nu volgt de voorwaarde $a+b=4$.

 

 

Opgave 369 [niveau ooO]

Hoeveel getallen van 10 cijfers bestaan er met precies vier nullen, drie enen, twee tweeën en één drie? (Deze getallen beginnen niet met een nul.)

Oplossing (van Casper de With). Bekijk eerst hoe de nullen geplaatst kunnen worden. De vier nullen kunnen op negen plaatsen worden geplaatst (niet op de eerste plaats). Dat kan op \(\left(\begin{array}{c} 9 \\ 4 \end{array} \right) = 126\) manieren. Vervolgens plaatsen we de drie enen op de zes resterende plaatsen. Dat kan op \(\left(\begin{array}{c} 6 \\ 3 \end{array} \right) = 20\) manieren. Vervolgens plaatsen we de twee tweeën op de drie resterende plaatsen. Dit kan op \(\left(\begin{array}{c} 3 \\ 2 \end{array} \right) = 3\) manieren. Er is nog precies één plaats waar de drie kan staan. Het totaal aantal gevraagde getallen is dus \(\left(\begin{array}{c} 9 \\ 4 \end{array} \right) \cdot \left(\begin{array}{c} 6 \\ 3 \end{array} \right)\cdot \left(\begin{array}{c} 3 \\ 2 \end{array} \right)=7560\).