Inzenden kan alleen per e-mail. Stuur je oplossing (getypt of een scan of foto van een handgeschreven oplossing) naar [email protected]. Je ontvangt een automatisch antwoord zodra we je bericht hebben ontvangen.
Voorzie het antwoord van een duidelijke toelichting (dat wil zeggen: een berekening of een bewijs). Vermeld je naam en adres; leerlingen moeten ook hun klas en de naam van hun school vermelden.
Je inzending moet bij ons binnen zijn vóór 1 maart 2018.

Opgave 370 [niveau oOO]

Het getal A bestaat uit een even aantal 1-tjes, en het getal B bestaat uit half zoveel 4-en. Bewijs dat A + B + 1 steeds een kwadraat van een natuurlijk getal is.

 

Opgave 371 [niveau oOO]

We bekijken alle getallen met precies drie delers. 4 en 25 zijn voorbeelden van dergelijke getallen. Is het waar dat alle overige getallen met precies drie delers eindigen op een 1 of een 9?

 

Opgave 372 [niveau OOo]

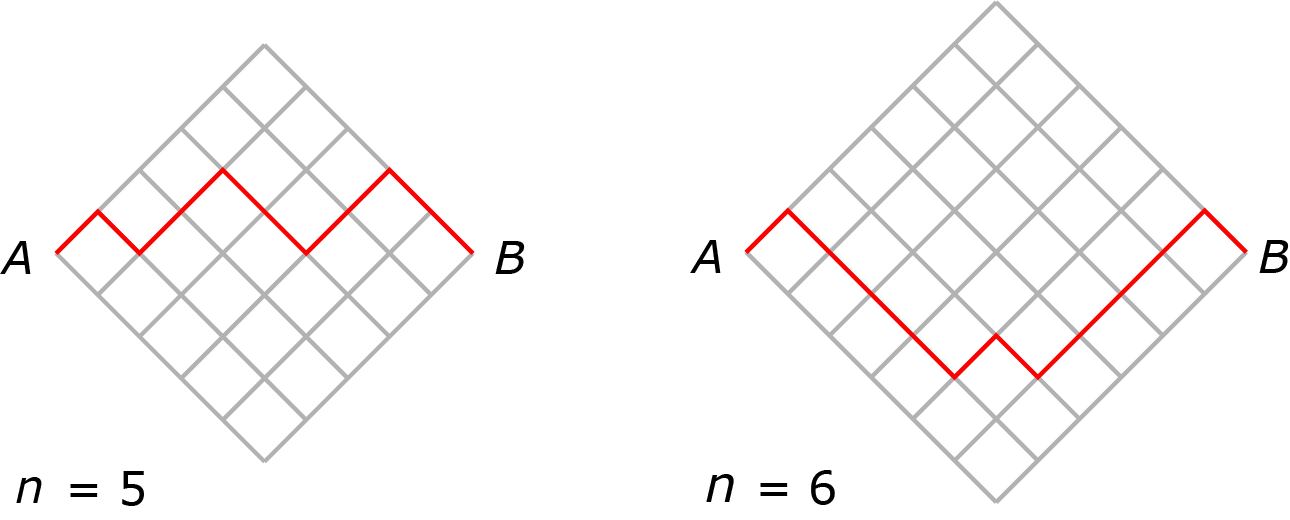
We stellen een berglandschap erg simplistisch voor, door middel van een rooster. In de afbeelding staan twee voorbeelden. De algemene regel is: Bij A gaat het berglandschap omhoog, om uiteindelijk te dalen tot B. Daar tussen is alles mogelijk, als het landschap maar roosterlijnen volgt en er precies 3 bergtoppen zijn. Hoeveel van dergelijke berglandschappen zijn er mogelijk voor $n \in \{1, 2, 3, 4, 5, 6, 7\}$ ?

 

Opgave 373 [niveau ooO]

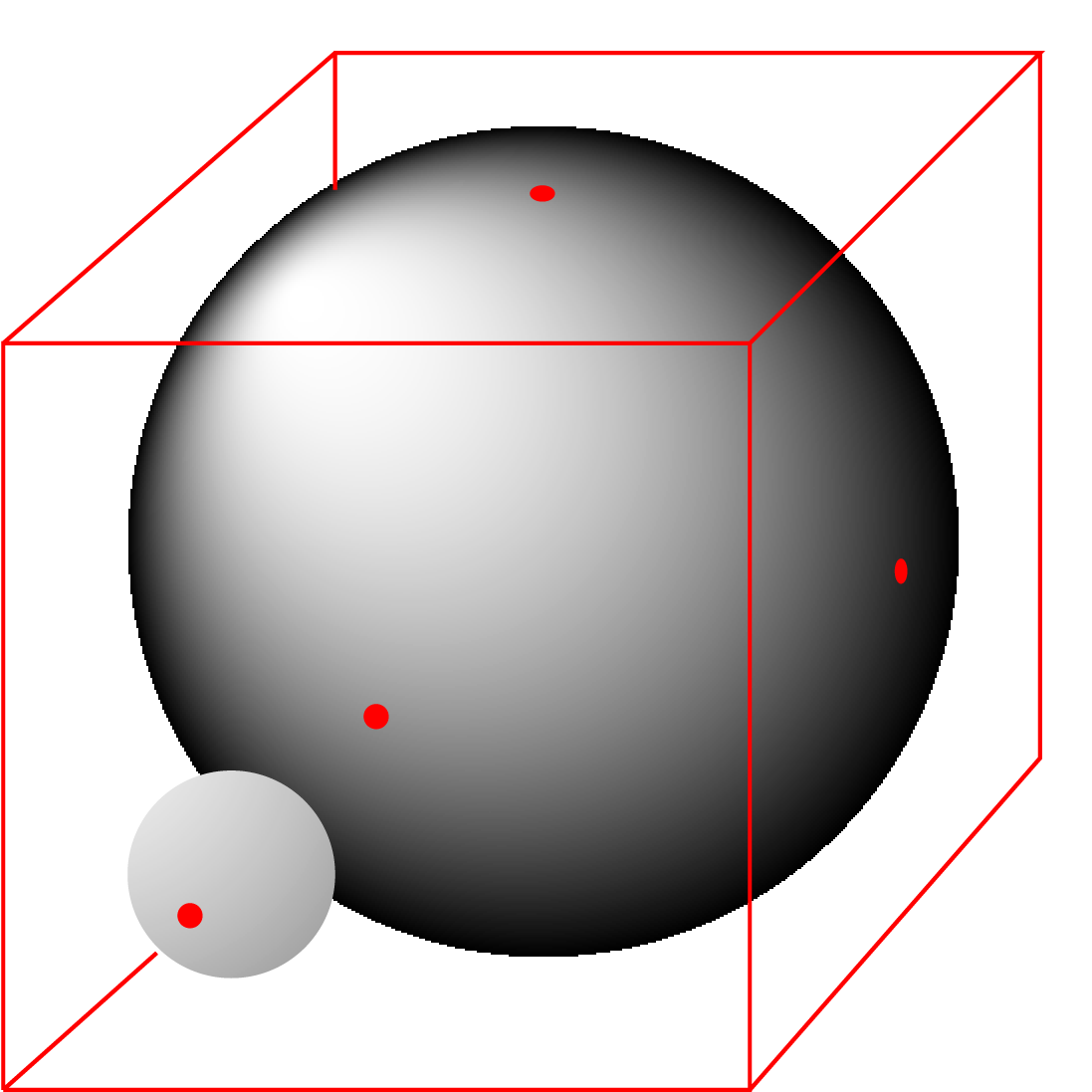
Je ziet hier een kubus met ribbe 2. In de kubus past een bol met straal 1, die alle 6 de zijvlakken raakt. In één van de hoekpunten willen we een kleinere bol plaatsen, die aan de bol en aan drie zijvlakken raakt. Wat is de straal van deze kleinere bol?

 

 

 

Bekijk oplossing