Oplossing 370 [niveau oOO]

Het getal $A$ bestaat uit een even aantal $1$-tjes, en het getal $B$ bestaat uit half zoveel $4$-en. Bewijs dat $A+ B + 1$ steeds een kwadraat van een natuurlijk getal is.
Oplossing. We gebruiken $A = \frac19 ⋅ (10^{2n} – 1) + \frac49 ⋅ (10^n – 1) + 1$. Er geldt $9A = 10^{2n} + 4 ⋅ 10^n + 4 = (10^n + 2)^2$. Ofwel voor $C = \frac13 ⋅ (10^n + 2)$ geldt $C^2 = A$. $C – 1$ bestaat uit even veel $3$-en als dat $B$ bestaat uit $4$-en.

Oplossing 371 [niveau oOO]

We bekijken alle getallen met precies drie delers. 4 en 25 zijn voorbeelden van dergelijke getallen. Is het waar dat alle overige getallen met precies drie delers eindigen op een 1 of een 9? 
Oplossing. Elk getal dat twee verschillende en ook onderling ondeelbaar (ofwel relatief priem) delers bevat, zeg $m$ en $n$ heeft minimaal $4$ delers, te weten $1$, $m$, $n$ en $mn$. De getallen die we zoeken mogen dus slechts één priemgetal als deler hebben. Het aantal delers van het getal $n = p^k$ is $k + 1$, namelijk $1$, $p$, $p^2$, $p^3, …, p^k$. Zodoende zijn getallen met precies drie delers getallen die een kwadraat zijn van een priemgetal, zoals $4$ en $25$. Behalve $2$ en $5$ eindigen alle priemgetallen op $1$, $3$, $7$ of $9$. De kwadraten van deze priemgetallen eindigen op $1$ of $9$. Dit is precies conform hetgeen bewezen moet worden.

Opgave 372 [niveau ooO]

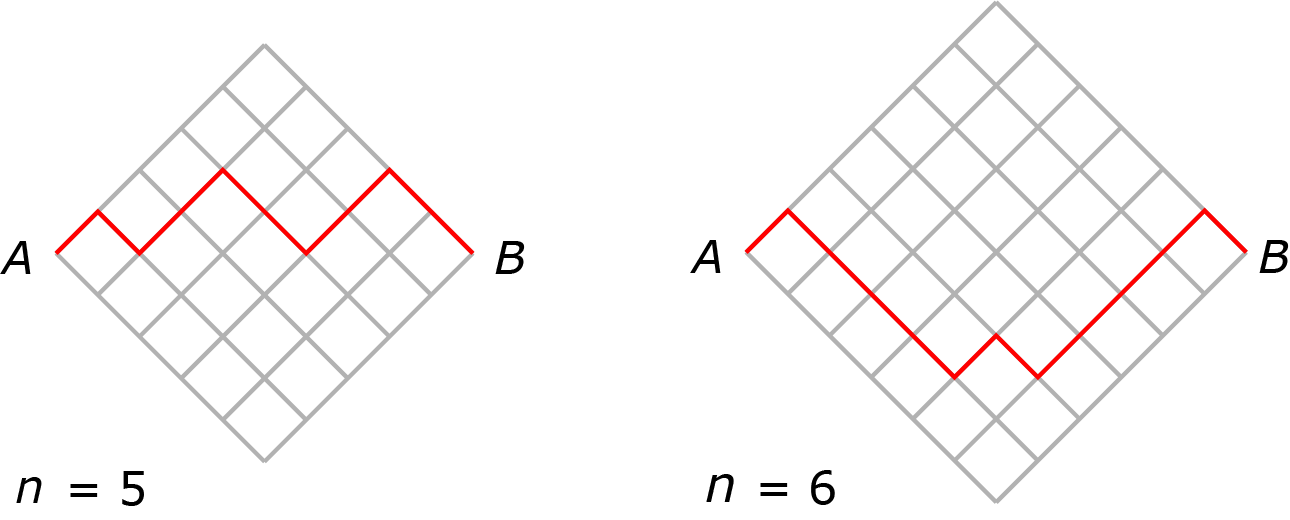
We stellen een berglandschap erg simplistisch voor, door middel van een rooster. In de afbeelding staan twee voorbeelden. De algemene regel is: Bij A gaat het berglandschap omhoog, om uiteindelijk te dalen tot B. Daar tussen is alles mogelijk, als het landschap maar roosterlijnen volgt en er precies 3 bergtoppen zijn. Hoeveel van dergelijke berglandschappen zijn er mogelijk voor $n \in \{1, 2, 3, 4, 5, 6, 7\}$ ?
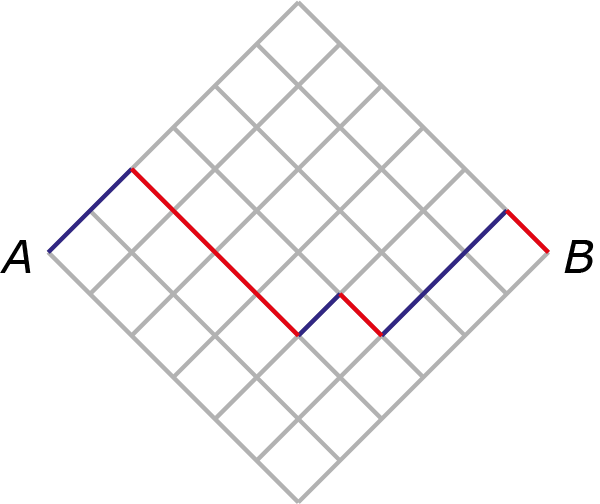Oplossing. We lopen van $A$ naar $B$. We kleuren de lijnen blauw als we omhoog lopen (van linksonder naar rechtsboven), we markeren de lijnen rood als we omlaag lopen (van linksboven naar rechtsonder). We hebben precies $3$ blauwe lijnstukken met totale lengte $n$, en eveneens $3$ rode lijnstukken met totale lengte $n$. Voor elke keuze van de blauwe en rode lijnstukken hebben we een ander berglandschap. 

Het is nu nog de vraag op hoeveel manieren kunnen we de blauwe en rode lijnstukken kiezen. 

Als het eerste lijnstuk lengte $n – 2$ heeft dan hebben de andere lijnstukken allebei lengte $1$. Als het eerste lijnstuk lengte $n – 3$ heeft, dan zijn er $2$ mogelijkheden $1 + 2$ of $2 + 1$. Voor $n – 4$ zijn er $3$ mogelijkheden $1 + 3$, $2 + 2$ en $3 + 1$. Uiteindelijk moet het eerste lijnstuk minimaal lengte $1$ hebben. Dan zijn er voor de twee andere lijnstukken precies $n – 2$ mogelijkheden. Het totaal aantal mogelijkheden is $1 + 2 + 3 + … + n – 2 = \frac12 (n – 2)(n – 1)$. Voor een berglandschap met drie toppen op een $n × n$ rooster zijn $\frac14 (n – 2)^2(n – 1)^2$ mogelijkheden. Voor $3$ t/m $7$ zijn dat respectievelijk $1$, $9$, $36$, $100$ en $225$ mogelijkheden.

 

Opgave 373 [niveau ooO]

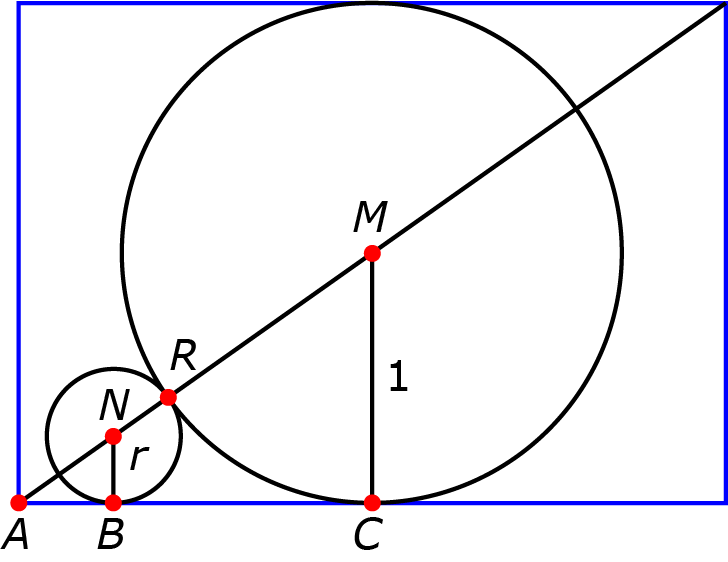
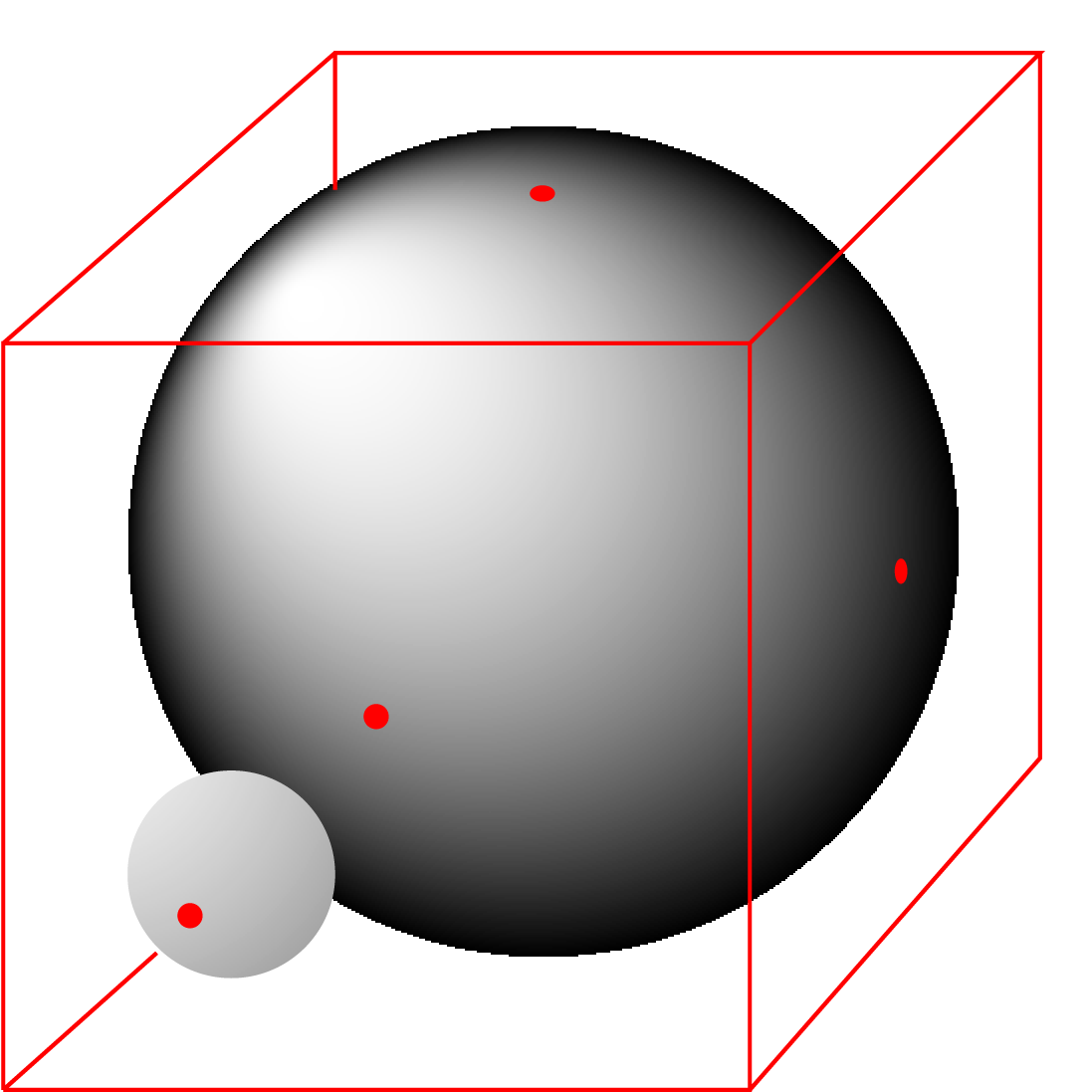
Je ziet hier een kubus met ribbe 2. In de kubus past een bol met straal 1, die alle 6 de zijvlakken raakt. In één van de hoekpunten willen we een kleinere bol plaatsen, die aan de bol en aan drie zijvlakken raakt. Wat is de straal van deze kleinere bol? 
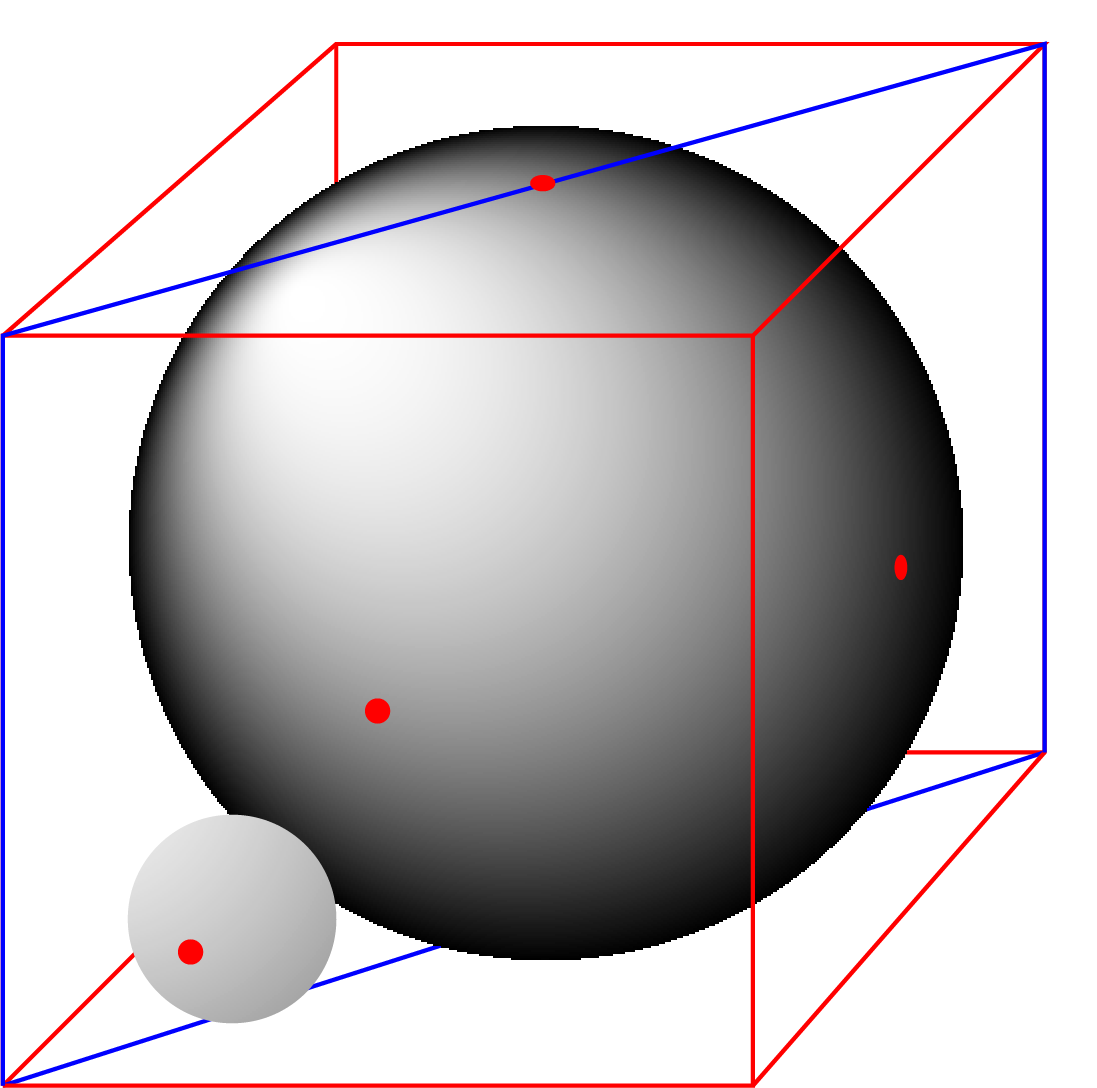Oplossing. In de kubus met de twee bollen bekijken we het blauwe vlak, het vlak dat verticaal staat en het bovenvlak volgens een diagonaal snijdt. Het tweede figuur geeft een doorsnede weer. $M$ is het middelpunt van de grote bol, $N$ is het middelpunt van de kleine bol, $C$ is het raakpunt van de grote bol op het ondervlak, $B$ is het raakpunt van de kleine bol op het ondervlak en $R$ is het raakpunt van de grote en kleine bol. Er geldt $|AC| = \sqrt2$. Volgens Pythagoras geldt $|AM| = \sqrt3$.
We noemen $r$ de straal van de kleine bol. Aangezien de driehoeken $\triangle ACM$ en $\triangle ABN$ gelijkvormig zijn moet gelden dat $|AN| = r\sqrt3$. Maar ook geldt |AM| = |AN| + |NR| + |RM| ofwel $\sqrt3 = r\sqrt3 + r + 1$. Hieruit volgt $r = \frac{\sqrt3-1}{\sqrt3+1} = 2 - \sqrt3$.