Inzenden kan alleen per e-mail. Stuur je oplossing (getypt of een scan of foto van een handgeschreven oplossing) naar [email protected]. Je ontvangt een automatisch antwoord zodra we je bericht hebben ontvangen.
Voorzie het antwoord van een duidelijke toelichting (dat wil zeggen: een berekening of een bewijs). Vermeld je naam en adres; leerlingen moeten ook hun klas en de naam van hun school vermelden.
Je inzending moet bij ons binnen zijn vóór 15 juli 2018.

 

Opgave 374 [niveau oOO]

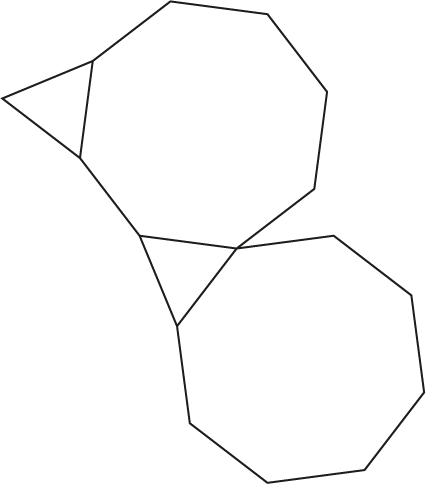Hiernaast is een schets met twee regelmatige achthoeken en twee gelijkzijdige driehoeken. Je kunt je voorstellen dat je dit patroon herhaalt. Kom je dan precies bij het begin uit?
Bonuspunt
Voor welke regelmatige $n$–hoek ($n > 6$) kun je een patroon creëren waarbij je precies terugkeert bij het begin?

 

Opgave 375 [niveau oOO]

Toon aan dat  $n^4 - 14n^3 + 35n^2 + 50n + 24$ voor positief gehele $n$ altijd deelbaar is door $24$.

 

Opgave 376 [niveau ooO]

Je komt Alex, Bert en Cor tegen. Zij hebben allen een geldbedrag bij zich, steeds bij allen bekend en al deze drie bedragen zijn verschillend. Verder spreekt van deze drie jongens één altijd de waarheid, één liegt altijd en de laatste wisselt waarheid spreken en liegen af.
Ze zeggen allen iets tegen jou:

Alex: Bert heeft meer geld op zak dan Cor.
Bert: Alex heeft meer geld op zak dan Cor.
Cor: Alex heeft meer geld op zak dan Bert.

Je denkt na en concludeert dat je niet kunt nagaan wie het meeste geld bij zich heeft. Daarom zeggen ze allen nog iets:

Alex: De uitspraak die Bert deed was correct.
Bert: Tot op heden telde ik precies twee correcte uitspraken.
Cor: Alex heeft meer geld op zak dan Bert.

Wie heeft het meeste geld op zak?

 

Opgave 377 [niveau ooO]

Bepaal alle positieve gehele getallen $x$ zodat ${x \over 4}+{9 \over x}$ een geheel getal is.

Bekijk oplossing