Opgave 374 [niveau oOO]

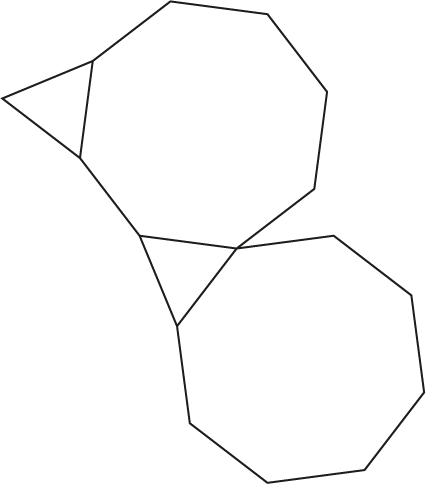Hiernaast is een schets met twee regelmatige achthoeken en twee gelijkzijdige driehoeken. Je kunt je voorstellen dat je dit patroon herhaalt. Kom je dan precies bij het begin uit?
Bonuspunt
Voor welke regelmatige $n$–hoek ($n > 6$) kun je een patroon creëren waarbij je precies terugkeert bij het begin?
Oplossing. Voor een $n$-hoek geldt: de som van de hoeken is $(n – 2) ⋅ 180°$. In het bijzonder voor een regelmatige achthoek is de som van de hoeken $1080°$, ofwel per hoek $135°$.
Bekijk nu een punt waar de gelijkzijdige driehoek (drie hoeken van 60°) en de regelmatige achthoek raken aan de veelhoek. Deze hoek is overal hetzelfde. Het wordt dus een regelmatige veelhoek. We berekenen de hoek $360° – 135° – 60° = 165° = 180° ⋅ (n-2)/n$. We vinden $\frac{360°}{n} = 15°$ , ofwel $n = 24$. De grote veelhoek heeft $24$ hoeken.

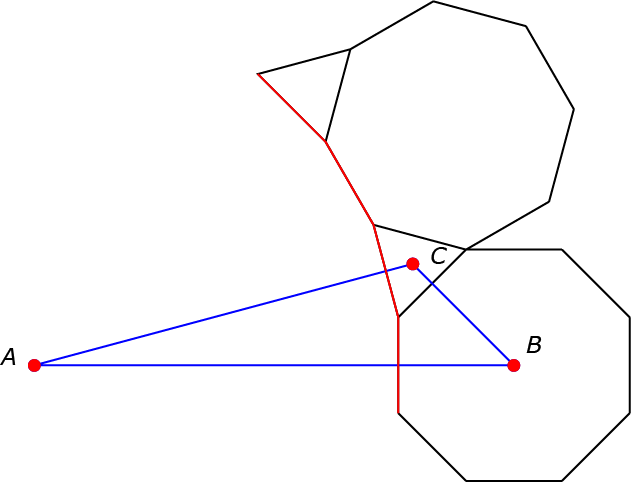Voor het bonuspunt moeten we uitgaan van een regelmatige $n$-hoek die we steeds combineren met een gelijkzijdige driehoek. Beschouw $\Delta ABC$. Hoekpunt $A$ is het middelpunt van de regelmatige $m$-hoek. Hoekpunt $B$ is het middelpunt van de regelmatige $n$-hoek. Hoekpunt $C$ is het middelpunt van de gelijkzijdige driehoek. $\angle A = \frac{360°}{m}$, $\angle B = \frac{360°}{n}$, en $\angle C = 120°$. Aangezien de som van de hoeken $180°$ is, moet gelden $\frac{360°}{m}+\frac{360°}{n}=60°$, ofwel $\frac1m+\frac1n=\frac16$. Verder moeten $m$ en $n$ geheel zijn. Bovendien moet $m$ even zijn, omdat een zijde afwisselend een driehoek en een $n$-hoek raakt. 
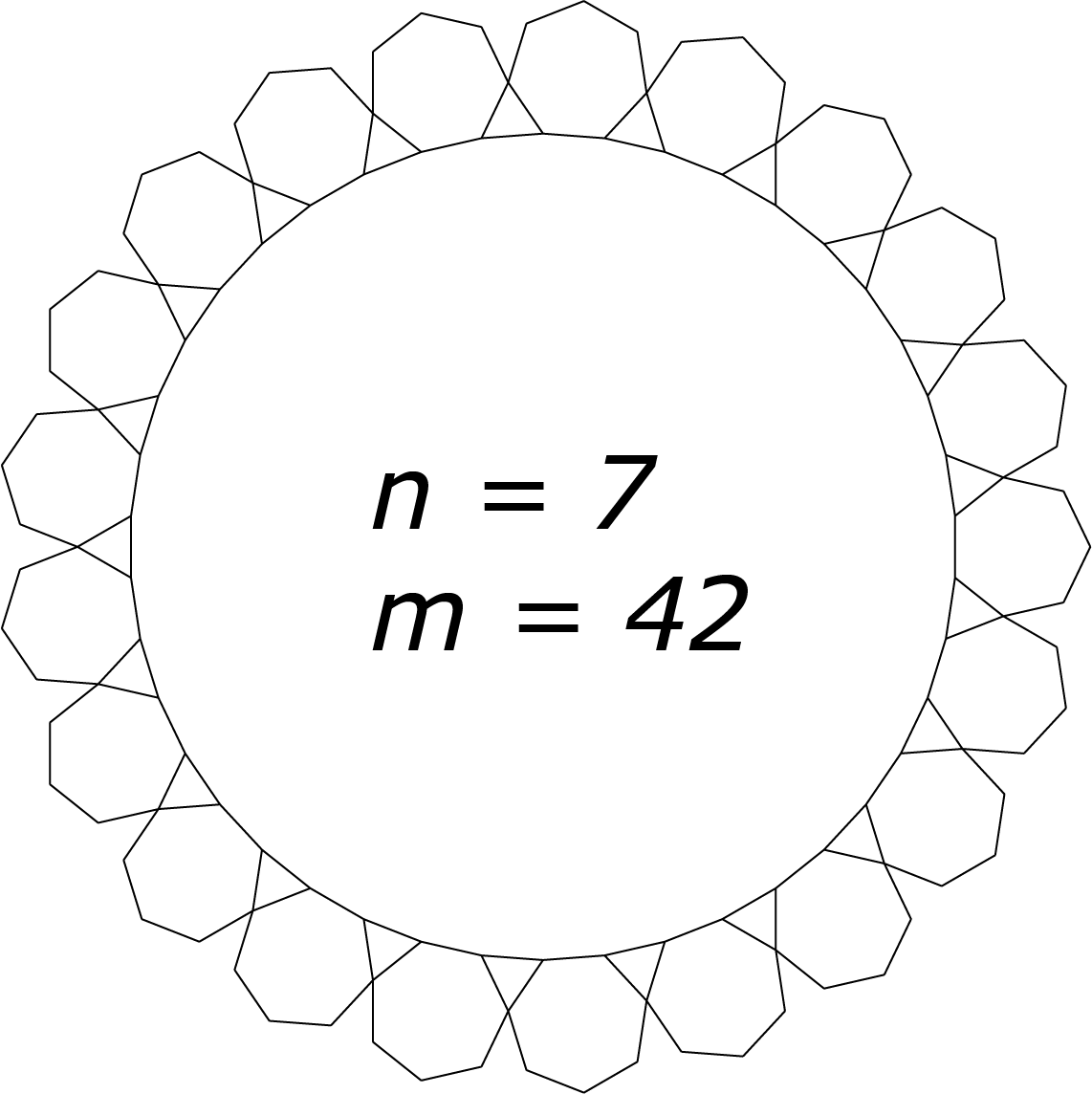
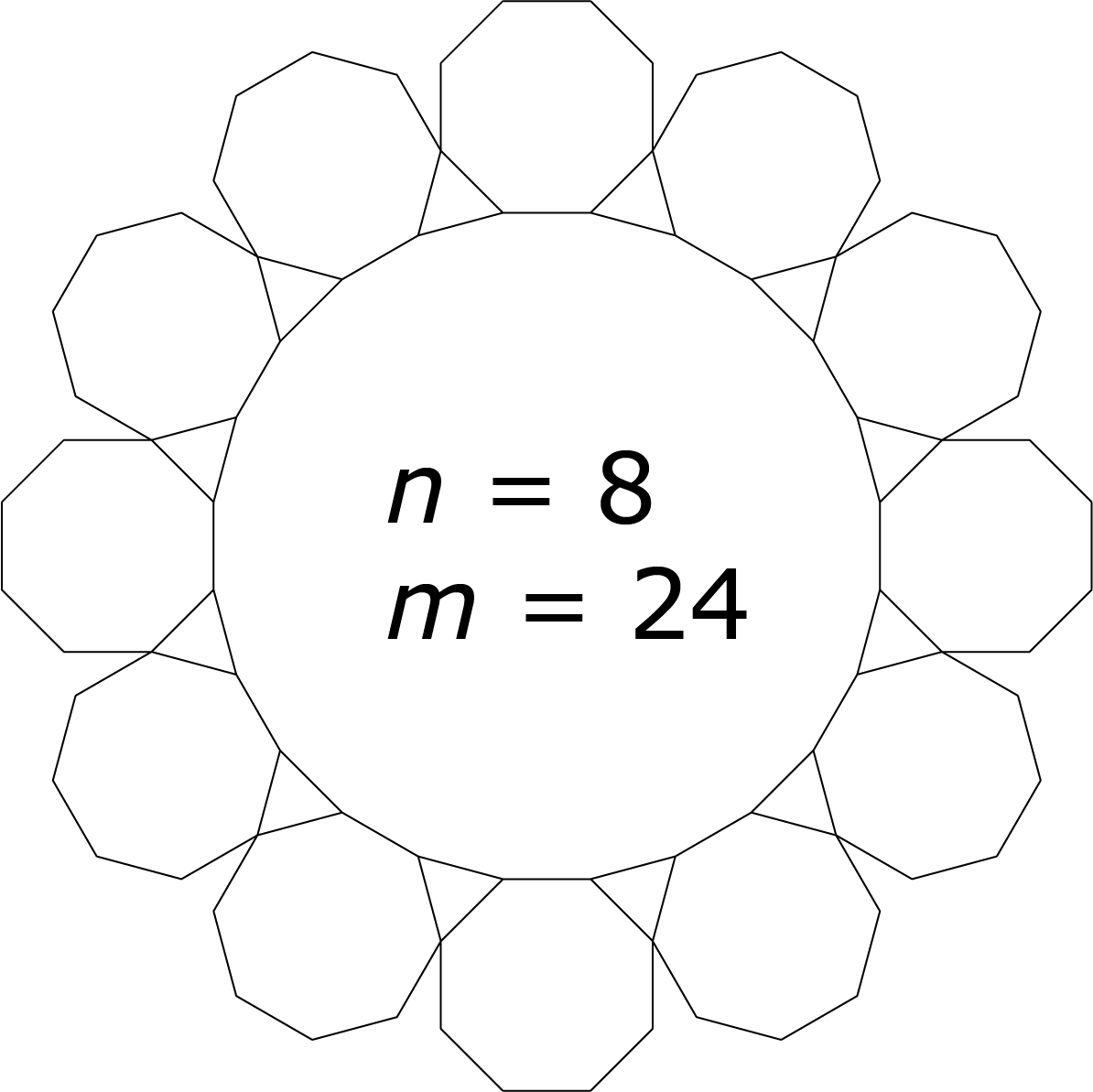
Probeer voor $m$ de waarden $8$, $10$ en $12$ en bereken de bijbehorende waarde voor $n$. Probeer voor $n$ de waarden $7$, $8$, $9$, $10$ en $11$ en bereken de bijbehorende waarde voor $m$. Voor $n = 11$ vinden we geen gehele waarde voor $m$. Voor $n = 10$ vinden we een oneven waarde voor $m$. De oplossingen zijn $n ∈ \{7, 8, 9, 12, 15, 24\}$ met bijbehorende $m ∈\{42, 24, 18, 12, 10, 8\}$. Zie de figuren hieronder. In de gevallen dat $m > 12$ overlappen de $n$-hoeken. Dat was voor een aantal inzenders een reden om deze oplossingen niet mee te tellen.

 

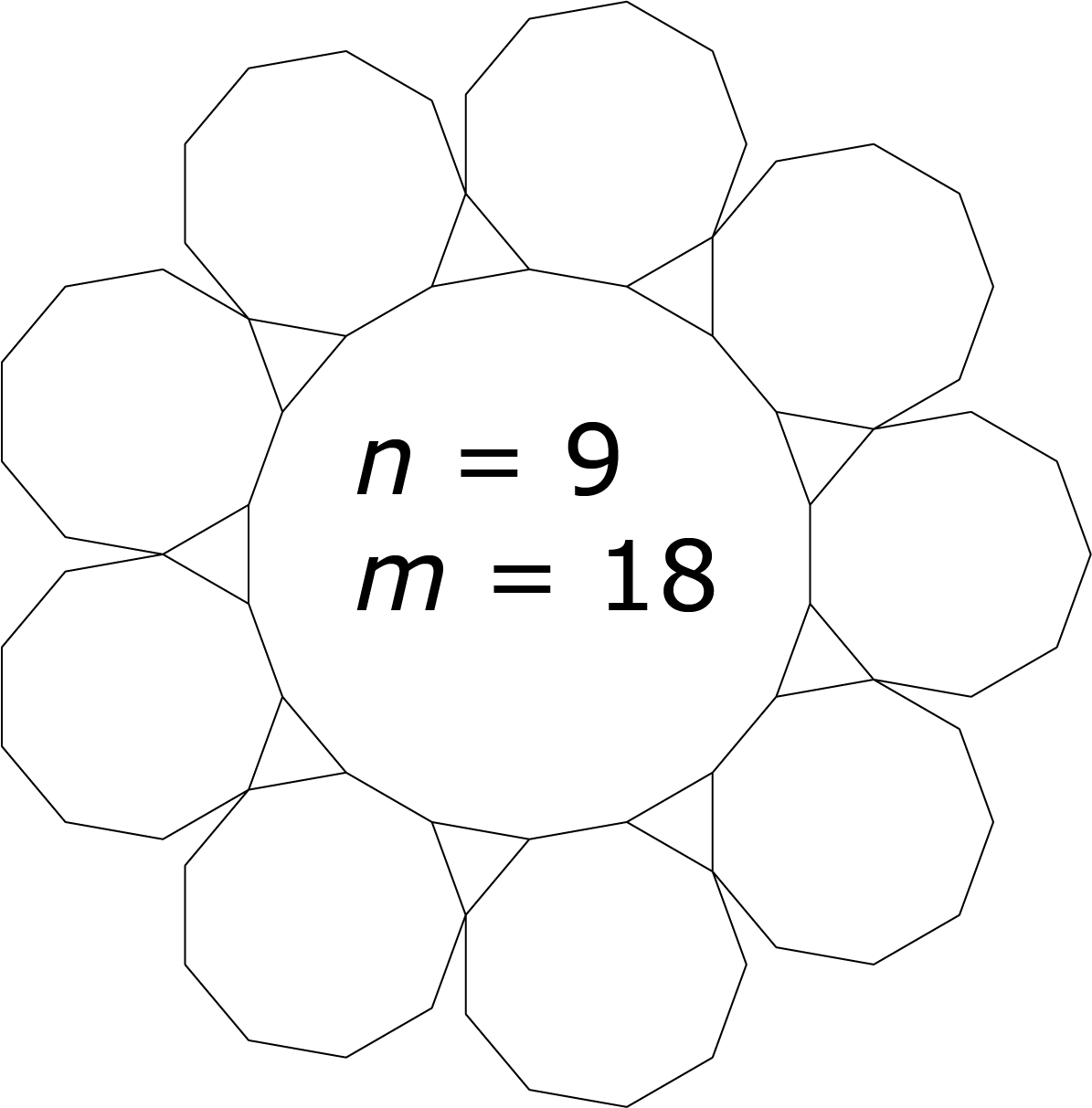
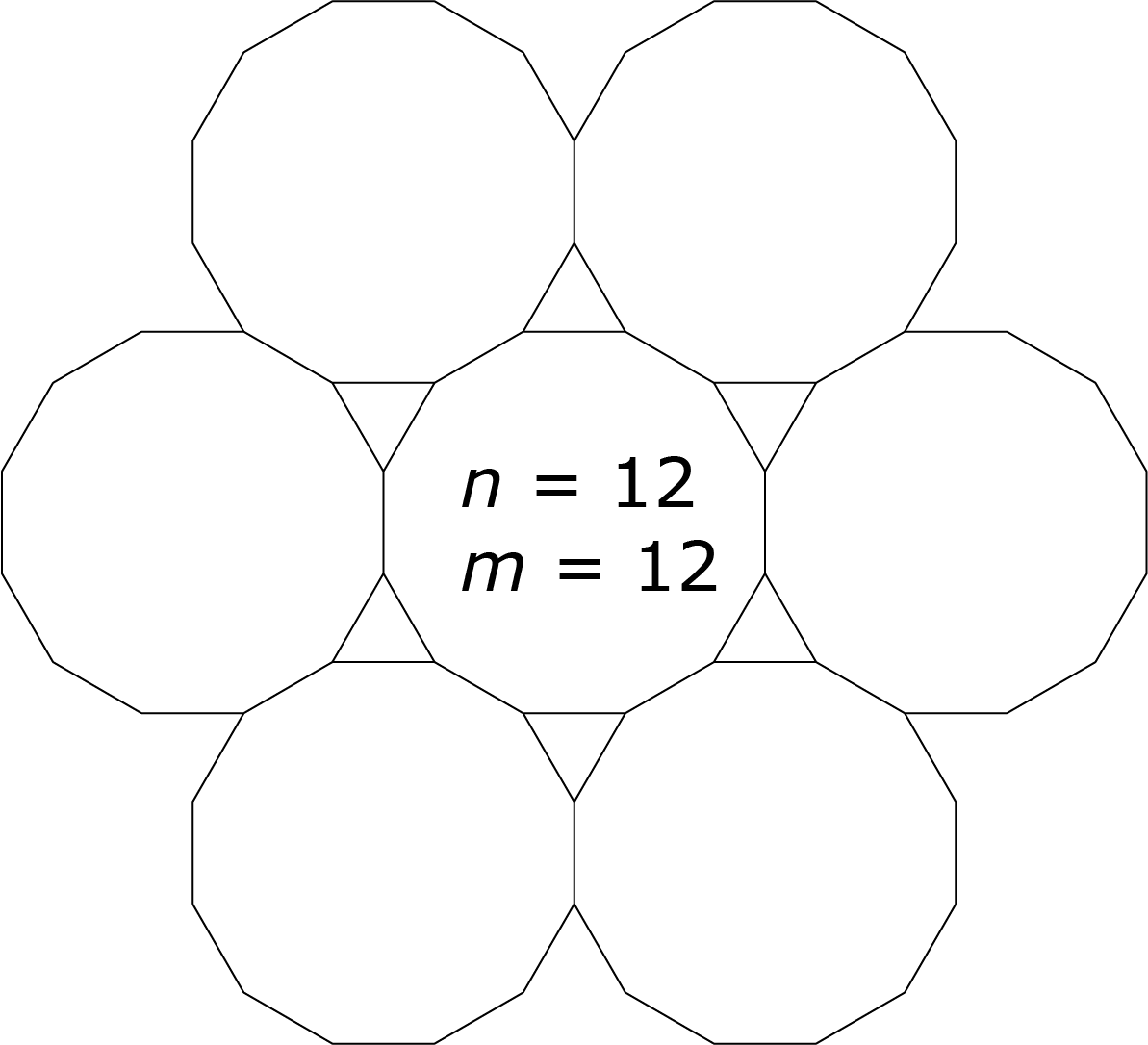
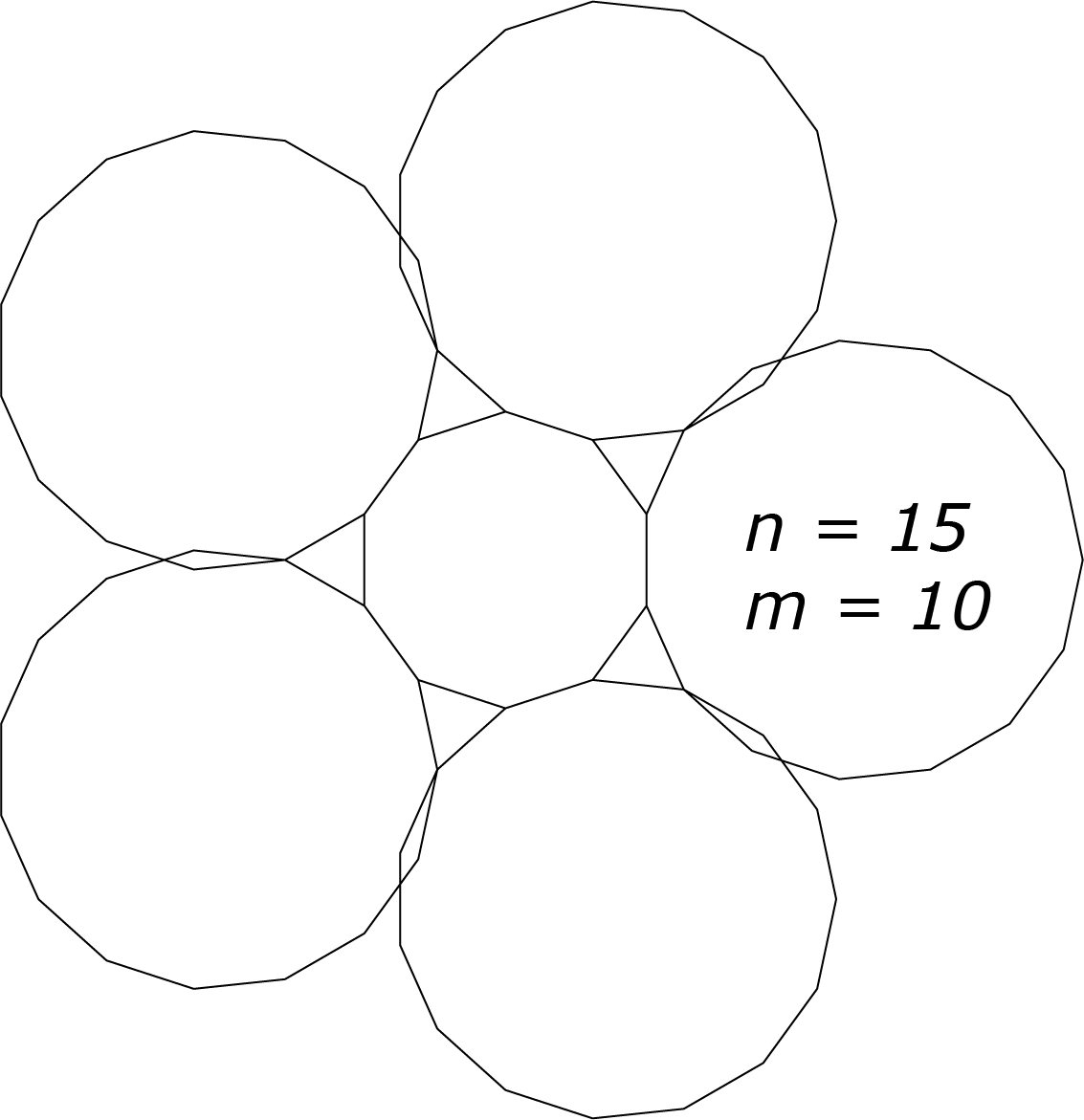
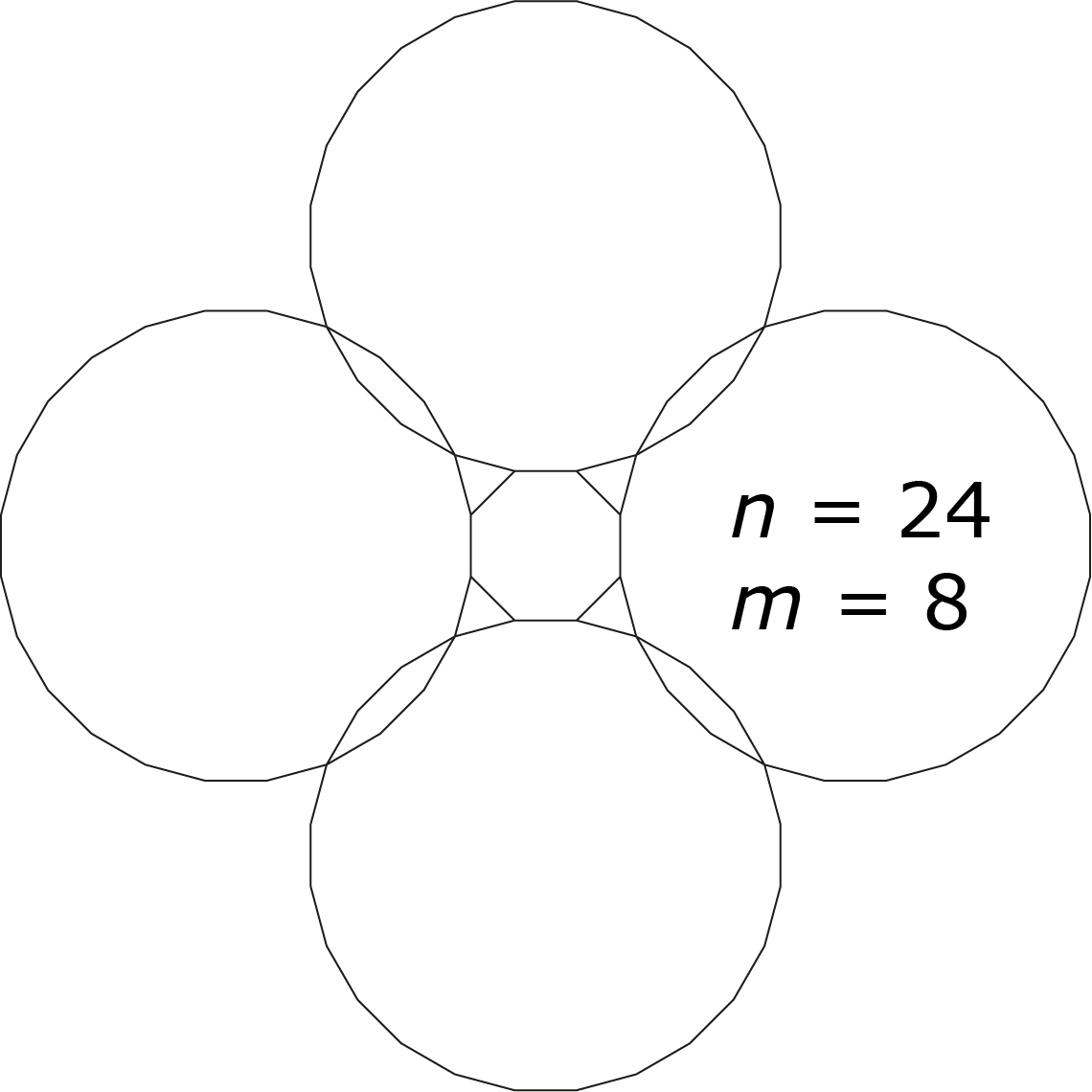
Opgave 375 [niveau oOO]

Toon aan dat $n^4 - 14n^3 + 35n^2 + 50n + 24$ voor positief gehele $n$ altijd deelbaar is door $24$.

Oplossing. We bekijken het polynoom $f(n) = n^4 – 14n^3 + 35n^2 + 50n$. (Dat is $24$ minder dan het gegeven polynoom.) Het polynoom $f(n)$ is te schrijven als $f(n) = n(n +1)(n – 5)(n – 10)$. Het volstaat om aan te tonen dat $f(n)$ zowel deelbaar is door $3$ als door $8$ voor alle $n$, omdat $24$ het product is van $3$ en $8$ en omdat $3$ en $8$ geen gemeenschappelijke factoren hebben. Om na te gaan dat $3$ $f(n)$ deelt hoeven we maar drie gevallen na te gaan. Als $n = 3k$ dan is $f(n)$ deelbaar door $n$ ofwel $3k$, dus zeker deelbaar door $3$. Als $n = 3k + 1$ dan is $f(n)$ deelbaar door $n – 10$ ofwel $3k – 9$, dus zeker deelbaar door $3$. Ten slotte als $n = 3k + 2$ dan is $f(n)$ deelbaar door $n + 1$ ofwel $3k + 3$, dus zeker deelbaar door $3$. Om na te gaan dat $8$ $f(n)$ deelt moeten we vier gevallen na gaan. Als $n = 4k$ dan is $f(n)$ deelbaar door $n(n – 10)$ ofwel $4k(4k – 10)$, dus zeker deelbaar door $8$. Als $n = 4k + 1$ dan is $f(n)$ deelbaar door $(n + 1)(n – 5)$ ofwel $(4k + 2)(4k – 4)$, dus zeker deelbaar door $8$. Als $n = 4k + 2$ dan is $f(n)$ deelbaar door $n(n – 10)$ ofwel $(4k + 2)(4k – 8)$, dus zeker deelbaar door $8$. Ten slotte als $n = 4k + 3$ dan is $f(n)$ deelbaar door $(n + 1)(n – 5)$ ofwel $(4k + 4)(4k - 2)$, dus zeker deelbaar door $8$.

Opgave 376 [niveau ooO]

Je komt Alex, Bert en Cor tegen. Zij hebben allen een geldbedrag bij zich, steeds bij allen bekend en al deze drie bedragen zijn verschillend. Verder spreekt van deze drie jongens één altijd de waarheid, één liegt altijd en de laatste wisselt waarheid spreken en liegen af.
Ze zeggen allen iets tegen jou:

Alex: Bert heeft meer geld op zak dan Cor.
Bert: Alex heeft meer geld op zak dan Cor.
Cor: Alex heeft meer geld op zak dan Bert.

Je denkt na en concludeert dat je niet kunt nagaan wie het meeste geld bij zich heeft. Daarom zeggen ze allen nog iets:

Alex: De uitspraak die Bert deed was correct.
Bert: Tot op heden telde ik precies twee correcte uitspraken.
Cor: Alex heeft meer geld op zak dan Bert.

Wie heeft het meeste geld op zak?

Oplossing. Je kunt direct nagaan dat Cor niet de waarheid wisselt met liegen, want hij doet tweemaal dezelfde uitspraak die waar of onwaar is. Als Cor tweemaal de waarheid spreekt, dan zullen Alex en Bert samen eenmaal de waarheid spreken. Als de tweede uitspraak van Bert waar is, dan heeft voordien alleen Cor een correcte uitspraak gedaan, als Bert dan liegt, dan zijn er voordien twee correcte uitspraken geweest. Kortom Cor spreekt niet de waarheid.
We onderscheiden nu vier gevallen: Cor liegt, Alex spreekt de waarheid en Bert liegt eerst en spreekt dan de waarheid, afgekort tot A:WW, B:LW, C:LL. De andere drie mo- gelijkheden zijn A:WW, B:WL, C:LL; A:LW, B:WW, C:LL en A:WL, B:WW, C:LL. Per geval gaan we na of de verschillende uitspraken met elkaar in overeenstemming zijn. Om te beginnen moet de tweede uitspraak van Alex in overeenstemming zijn met de eerste uitspraak van Bert (ofwel beide waar of beide onwaar).
De waarheidstabel hieronder beschrijft de uitkomst.

Alex 1	Bert 1	Cor 1	Alex 2	Bert 2	Cor 2	Resultaat
W	L	L	W	W	L	Tweede uitspraak Alex klopt niet
W	W	L	W	L	L	C$<$B, C$<$A, A$<$B,
L	W	L	W	W	L	B$<$C, C$<$A, A$<$B,
W	W	L	L	W	L	Tweede uitspraak Alex klopt niet

Bert heeft dus het meeste geld bij zich.

 

Opgave 377 [niveau ooO]

Bepaal alle positieve gehele getallen $x$ zodat ${x \over 4}+{9 \over x}$ een geheel getal is.
Oplossing. We herschrijven de opgave tot de vergelijking $${x \over 4}+{9 \over x}=n$$ We vermenigvuldigen beide zijden van de vergelijking met $4x$. We vinden: $x^2 + 36 = 4nx$ ofwel $36 = x(4n - x)$. Kies voor $x$ de opeenvolgende delers van $36$ en ga na of $n$ dan geheel is. We vinden $x \in \{2, 6, 18\}$.